Binomlar - Mathority

Bu sayfada binomun ne olduğuna dair bir açıklama bulacaksınız ve ayrıca her bir binom türünün örneklerini görebileceksiniz. Ayrıca, binomlarla işlemleri çözmek için kullanılan formülleri de gösteriyoruz: binomların çarpımı, binom karesi, binom küpü,…

Bir çift nedir?

Cebirde binomun tanımı şöyledir:

Binom yalnızca iki tek terimden oluşan bir polinomdur . Başka bir deyişle, bir binom, artı işareti (+) veya eksi işareti (-) ile birleştirilen yalnızca 2 farklı terimden oluşan cebirsel bir ifadeden oluşur.

Binom kelimesi Yunancadan gelir ve iki sözcüksel bileşenden ( bi ve nomos ) oluşur; bunlar şu anlama gelir:

bi : 2 anlamına gelen önek.
nomos : parça anlamına gelir.

Bu nedenle binomun anlamını çıkarabiliriz: iki parçalı (veya 2 tek terimli) polinom.

Öte yandan çift kavramının matematiksel anlamının dışında başka bir anlamı daha vardır; yani bir çift aynı zamanda siyasi yaşamda, bazı spor disiplinlerinde ve hatta eğlencede öncü rol oynayan iki kişiliği de ifade edebilir. . Ancak tabii ki burada binomun matematiksel tanımına odaklanacağız.

Binom örnekleri

Binom kavramını anlamayı tamamlamak için bu tür polinomun birkaç örneğini göreceğiz:

İkinci dereceden binom örneği:

$x^2+4x$

Üçüncü dereceden binom örneği:

$x^3+5$

Dördüncü derece binom örneği:

$3x^4+8x^2$

Artık binomun ne olduğunu bildiğimize göre, farklı binom türlerinin olduğunu ve binomlarla işlemlerin nasıl çözüldüğünü göreceğiz.

binom karesi

Kare binom , dikkate değer bir çarpım veya dikkate değer eşitlik olarak da adlandırılan dikkate değer bir özdeşliktir. 2’ye yükseltilmiş bir binomun kuvvetinin çözümü, bunun toplam binom mu yoksa fark binom mu olduğuna bağlıdır.

Toplam binom, iki terimi pozitif olan binom anlamına gelir, yani kare toplamlı binom:

$(a+b)^2$

Öte yandan, bir fark (veya çıkarma) binom’u, toplama binomunun eşleniğidir, yani monomlarından birinin negatif işareti vardır. Bu nedenle, kare binom farkının cebirsel ifadesi şöyledir:

$(a-b)^2$

Kareli bir binom hesaplamak için, gördüğümüz gibi, toplama veya çıkarma olmasına bağlı olarak değişen bir formül uygulamanız gerekir. Bunun nasıl yapıldığını dikkate değer eşitlik formüllerinde öğrenin; burada tüm adım adım açıklamaları, örnekleri ve çözülmüş alıştırmaları ve yalnızca bu 2 önemli eşitliği değil hepsini görebilirsiniz.

binom küp

Daha az sıklıkla kullanılmasına rağmen küp binomları da dikkate değer ürünler olarak kabul edilir. Veya başka bir deyişle, bir binomun küpünü hızlı bir şekilde bulmanızı sağlayan matematik kuralları vardır (bunları yukarıdaki önemli özdeşlik formülleri bağlantısında görebilirsiniz).

Daha önce olduğu gibi, bu potansiyelleştirmenin sonucu, bunun bir toplamın küpü olup olmadığına bağlıdır:

$(a+b)^3$

Ya da tam tersine kuvvet bir farkın ya da çıkarmanın küpünden oluşuyorsa:

$(a-b)^3$

Mantıksal olarak, kareli bir binom ile küplü bir binom arasındaki temel fark, kuvvet üssüdür. Bununla birlikte, küp şeklinde bir binomun formülü, kareli bir binomun formülünden çok daha karmaşıktır.

dikkate değer anlaşmalar

Daha az bilinen dikkate değer kimliklere (veya dikkate değer ürünlere) karşılık geldikleri için, özellikleri nedeniyle biraz özel olan belirli binom türleri vardır.

Karelerin toplamı:
$a^2+b^2$
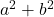
Karelerin farkı (veya çıkarılması):
$a^2-b^2$
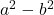
Küplerin toplamı:
$a^3+b^3$
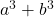
Küplerin farkı (veya çıkarılması):
$a^3-b^3$

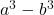
Altın

$a$

$b$

herhangi iki tek terimlidir.

Her ne kadar bu binom ifadeleri yukarıda gördüklerimize çok benzese de (binom karesi ve binom küpü), eğer yakından bakarsanız farklıdırlar. Bu anlamda dikkate değer binomların formüllerini ve bunların çıkarımlarını da yukarıdaki bağlantıya tıklayarak ⬆ dikkate değer kimliklerin formüllerini görebilirsiniz.⬆

binom çarpımı

Binomlarla en sık yapılan işlemlerden biri çarpmadır. Şimdi iki terimli sayılar arasındaki çarpımın nasıl hesaplanacağına dair bir örnek göreceğiz.

$(x^2+2x)\cdot (x-5)$

Binom çarpımını hesaplamak için ilk önce birinci binomdaki her terimi ikinci binomdaki her terimle çarpmamız gerekir:

$x^2\cdot x+x^2\cdot (-5)+2x\cdot x +2x\cdot (-5)$

$x^3-5x^2+2x^2 -10x$

Daha sonra benzer terimleri gruplandırıyoruz, yani aynı gerçek kısma sahipler:

$\bm{x^3-3x^2 -10x}$

Ve bu şekilde çiftler arasındaki çarpımın sonucunu bulmayı başardık.

Ortak terimli iki binomun çarpımı

Çarpmaya katılan binomların ortak terimi değişken olduğunda

$x,$

Bu binom işlemini hızlı bir şekilde hesaplamak için bir formül var:

$(x+a)(x+b) = x^2+(a+b)x+ab$

Burada size çözülmüş bir alıştırma gösteriyoruz, böylece bu formülü nasıl uygulayacağınızı görebilirsiniz:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

Newton’un iki terimlisi

Binom teoremi olarak da adlandırılan Newton’un binom’u , binomların kuvvetlerini hesaplamak için kullanılan bir formüldür.

Newton binomunun matematiksel formülü aşağıdaki gibidir:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}x^{n-k}y^k$

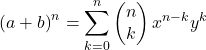
Veya eşdeğer:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

Gördüğünüz gibi bu formülü anlamak biraz karmaşık. Bu yüzden daha iyi anlayabilmeniz için en düşük derecedeki binomların kuvvetlerini aşağıda yaptık:

Bu formül, kare veya küp binomların hesaplanmasında biraz sıkıcı olabilir, çünkü yukarıda gördüğümüz gibi daha basit formüller de vardır. Bununla birlikte, Newton’un binom’u daha yüksek dereceli kuvvetleri bulmak için çok kullanışlıdır; örneğin, dördüncüye kadar bir binomun belirlenmesinde yaygın olarak kullanılır.

Ancak bu formülü uygulamak için bir kombinatoryal sayının, yani türün cebirsel ifadesinin nasıl hesaplanacağını bilmeniz gerekir.

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

, hesaplama kolay değil. 🔍Bu yüzden sağ üstteki arama motorumuzda bu işlemin nasıl yapıldığını aramanızı öneririz 🔎, bu işlemi sizlere adım adım anlattığımız yazımızı bulacaksınız.