Simetrik matris - Mathority

Bu sayfada simetrik matrislerin ne olduğuna dair açıklama bulacaksınız. Ayrıca, şüphe duymamanız için size birkaç örnekle birlikte bir matrisin simetrik olduğunu hızlı bir şekilde nasıl tanımlayacağınızı gösteriyoruz. Ayrıca simetrik matrislerin tüm özelliklerini de bulacaksınız. Ve son olarak, herhangi bir kare matrisin sahip olduğu belirli bir özelliği açıklıyoruz: Simetrik bir matris ve bir antisimetrik matrisin toplamına ayrıştırılabilir.

Simetrik matris nedir?

Simetrik bir matrisin tanımı aşağıdaki gibidir:

Simetrik bir matris, transpozu matrisin kendisine eşit olan bir kare matristir.

$A^t = A$

Altın

$A^t$

transpoze matrisini temsil eder

$A$

Simetrik matris kavramını öğrendikten sonra herhangi bir simetrik matrisin nasıl kolayca tanımlanabileceğini göreceğiz:

Bir matris ne zaman simetriktir?

Simetrik bir matrisin yapısını tanımak çok basittir: i satırının ve j sütununun elemanı, j satırının ve i sütununun elemanıyla aynı olmalıdır. Ve matrisin ana köşegeninin değerleri herhangi biri olabilir.

Simetrik matris örnekleri

Anlamanıza yardımcı olacak birkaç simetrik matris örneği:

2 × 2 mertebesinden simetrik bir matris örneği

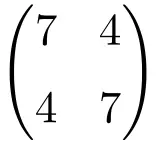
3×3 boyutlu simetrik matris örneği

4×4 boyutunda simetrik bir matris örneği

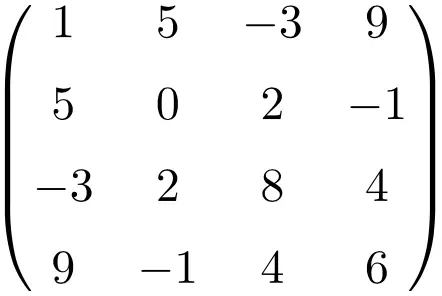
Bu üç matrisin transpoze edilmesiyle simetrik olduklarını doğrularız çünkü transpoze matrisler ilgili orijinal matrislere eşdeğerdir.

Neden buna simetrik matris deniyor?

Önceki örneklere yakından bakarsanız, simetrik bir matrisin ana köşegeni bir simetri eksenidir, yani köşegenin üstündeki sayılar ile altındaki sayılar arasında ayna görevi görür. Bu nedenle bu tür matrislere simetrik matrisler denir.

Simetrik matrislerin özellikleri

Simetrik matrislerin özellikleri aşağıdaki gibidir:

İki simetrik matrisin eklenmesi (veya çıkarılması) başka bir simetrik matris verir. Toplanan (veya çıkarılan) iki matrisin transpozisyonunun her matrisin ayrı ayrı transpozisyonuna eşdeğer olması nedeniyle:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

Herhangi bir simetrik matrisin bir skalerle çarpılması aynı zamanda başka bir simetrik matrisin ortaya çıkmasına neden olur.

Benzer şekilde, iki simetrik matris arasındaki matris çarpımı her zaman başka bir simetrik matrise eşit değildir, yalnızca ve ancak iki matrisin yer değiştirmesi durumunda. Bu durum, aktarılan matris çarpımı özelliği ile kanıtlanabilir:

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

Üs bir tamsayı olduğu sürece, simetrik bir matrisin kuvveti başka bir simetrik matrisin ortaya çıkmasına neden olur.

Açıkçası, üniter matris ve sıfır matrisi simetrik matrislerin örnekleridir.

Simetrik bir matrise uyumlu bir matris de simetrik olmalıdır.

Simetrik bir matris düzenli veya tersinirse, ters matrisi de simetriktir.

Simetrik bir matrisin ek matrisi için de durum aynıdır: Simetrik bir matrisin ek matrisi, çözüm olarak başka bir simetrik matris verir.

Gerçek bir simetrik matris aynı zamanda normal bir matristir.

Simetrik matrisler Hermit matrislerinin özel bir durumu olduğundan, simetrik bir matrisin tüm özdeğerleri (veya özdeğerleri) gerçek sayılardır.

Spektral teorem bize, elemanları gerçek olan tüm matrislerin köşegenleştirilebilir matrisler olduğunu ve ayrıca köşegenleştirmenin dik bir matris aracılığıyla gerçekleştirildiğini söyler. Bu nedenle, tüm gerçek simetrik matrisler dik köşegenleştirilmiştir.

Öte yandan, karmaşık sayılara sahip simetrik matrisler, üniter bir matris aracılığıyla köşegenleştirilebilir.

Hessian matrisi her zaman simetriktir.

Bir kare matrisin simetrik bir matrise ve bir antisimetrik matrise ayrıştırılması

Kare matrislerin özel bir özelliği, bir simetrik matris artı bir antisimetrik matrisin toplamına ayrıştırılabilmeleridir.

Bunu yapmamızı sağlayan formül şu şekildedir:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

C, ayrıştırmak istediğimiz kare matris olduğunda, C ^t’nin devriği yapılır ve son olarak S ve A, C matrisinin ayrıştırıldığı sırasıyla simetrik ve antisimetrik matrislerdir.

Aşağıda bunun nasıl yapıldığını görmek için çözülmüş bir alıştırma bulacaksınız. Aşağıdaki matrisi ayrıştıralım:

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

Simetrik ve antisimetrik matrisi aşağıdaki formüllerle hesaplıyoruz:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

Ve iki matrisi toplayarak denklemin yerine getirilip getirilmediğini kontrol edebiliriz:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅