Benzer veya benzer matrisler

Bu sayfada benzer matrisler olarak da adlandırılan benzer matrislerin açıklamasını bulacaksınız. Üstelik şüphe duymamanız için size iki benzer matrisin net bir örneğini ve bu tür matrislerin tüm özelliklerini gösteriyoruz. Son olarak, bunların uyumlu matrislerle nasıl ilişkili olduğunu bile görebileceksiniz.

Benzer (veya benzer) matrisler nelerdir?

Benzer matrislerin tanımı aşağıdaki gibidir:

iki matris

$A$

$B$

bir matris varsa benzerdir (veya benzerdir)

$P$

aşağıdaki koşul karşılanır:

$P^{-1}AP = B$

Veya eşdeğer:

$AP = PB$

Aslında matris

$P$

temel değişim matrisi görevi görür. Dolayısıyla bu denklemin anlamı matrisin

$A$

başka bir tabanda ifade edilebilir (

$P$

), bu da matrisi doğurur

$B$

Aslında matrisi dönüştürdüğümüz için bu terime benzerlik dönüşümü de denilebilir.

$A$

matriste

$B$

Açıkçası matris

$P$

düzenli veya dejenere olmayan bir matris (sıfır olmayan determinant) olmalıdır.

Öte yandan iki matrisin aşağıdaki ifadeye benzer olduğunu belirtebiliriz:

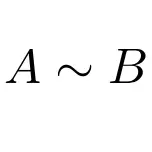
benzer veya benzer matrislerin açıklaması

Bu matris sınıfı doğrusal cebir için göründüğünden daha önemlidir. Bunlar esas olarak köşegenleştirilebilir matrisler için kullanılır, çünkü herhangi bir matrisi köşegenleştirme prosedürü matris benzerliği kavramına dayanır.

Aslında bir matrisin köşegenleştirilmesi işlemi, aynı zamanda köşegen bir matris olan benzer bir matrisin hesaplanmasını içerir. Bir matrisin köşegenleştirilmesi konusunda bunun nasıl yapıldığını görebilirsiniz.

Benzer veya benzer matrislere örnek

Daha sonra kavramı özümsemeyi tamamlamak için 2×2 boyutunda benzer matrislerin bir örneğini göreceğiz.

A ve B kare matrisleri, ters çevrilebilir P matrisi aracılığıyla birbirine benzer:

$\displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}$

$\displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}$

Bunların karşılıklı olarak benzer matrisler olduğunu göstermek için önce P’nin ters matrisini hesaplamalıyız:

$\displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}$

Şimdi iki matrisin benzerliğini tanımlayan matris çarpımını gerçekleştirerek benzer olup olmadıklarını kontrol ediyoruz:

$\displaystyle P^{-1}AP = B \quad ?$

$\displaystyle P^{-1}AP = B$

✅

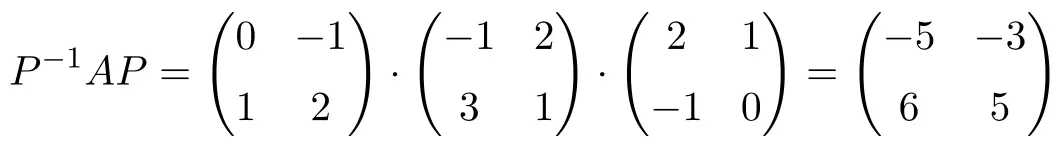
Evet benzerlik bağıntısı sağlandığı için benzer matrislerdir.

Benzer matris özellikleri

İki benzer matris A ve B aşağıdaki özellikleri paylaşır:

Aynı rütbe.

$rg(A)=rg(B)$

İki matrisin determinantları aynıdır.

$det(A)=det(B)$

Aynı izleme.

$tr(A)=tr(B)$

Aynı özdeğerler (veya özdeğerler). Ancak özvektörler (veya özvektörler) genellikle farklıdır.

Aynı karakteristik polinom ve minimum polinom.

Bir matrisin transpoze edilmesi orijinal matrise benzer.

B matrisi, A matrisinin satırlarına temel işlemler uygulanarak bulunabilir veya bunun tersi de geçerlidir.

Benzerliğin yansıtıldığı açıktır. Yani A, B’ye benzerse B de A’ya benzer.

Ayrıca matrislerin benzerliği de simetriktir. Başka bir deyişle, P matrisi ile A(B)’ye benzer bir matris elde edilebiliyorsa, aynı P matrisi ile B(A)’ya benzer bir matris de elde edilebilir:

$B=P^{-1}AP$

$A=PBP^{-1}$

Ayrıca benzerlik geçişlidir. Yani eğer A matrisi B matrisine ve B matrisi C matrisine benzerse, A matrisi de C matrisine benzer.

$\left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C$

Son olarak, her kalıp testere dişi kalıbına benzer. Ve bu özellikten şu sonucu çıkarabiliriz: her kare matris bir üçgen matrise benzer.

uyumlu matrisler

Öte yandan, matrisler arasında çok benzer bir ilişki daha vardır, ancak bu, ters matrisle olmak yerine, devrik matrisledir. Buna uyum denir .

Aşağıdaki eşitliğin sağlandığı ters çevrilebilir bir P matrisi varsa, A ve B iki matrisi uyumludur :

$P^tAP = B$

Gördüğünüz gibi, bu benzer matrislerin analoğudur ancak matrisin yeri değiştirilmiştir.

Benzer (veya benzer) matrisler nelerdir?

Benzer veya benzer matrislere örnek

Benzer matris özellikleri

uyumlu matrisler

Yorum bırakın Yanıtı iptal et