Teğetin türevi

Burada teğet fonksiyonunun nasıl türetildiğini öğreneceksiniz. Ayrıca tanjantın türevi örneklerini görebilecek ve hatta adım adım çözülen alıştırmalarla pratik yapabileceksiniz. Son olarak teğet türev formülünü de gösteriyoruz ve size ters teğet türev formülünü de gösteriyoruz.

Teğetin türevi nedir?

X’in tanjantının türevi, 1 bölü x’in kosinüsünün karesine eşittir. X’in tanjantının türevi aynı zamanda x’in sekantının karesine ve 1 artı x’in tanjantının karesine eşdeğerdir.

\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}

Tüm ifadeler eşdeğerdir, dolayısıyla teğet fonksiyonun onu türetmek için üç olası formülü vardır.

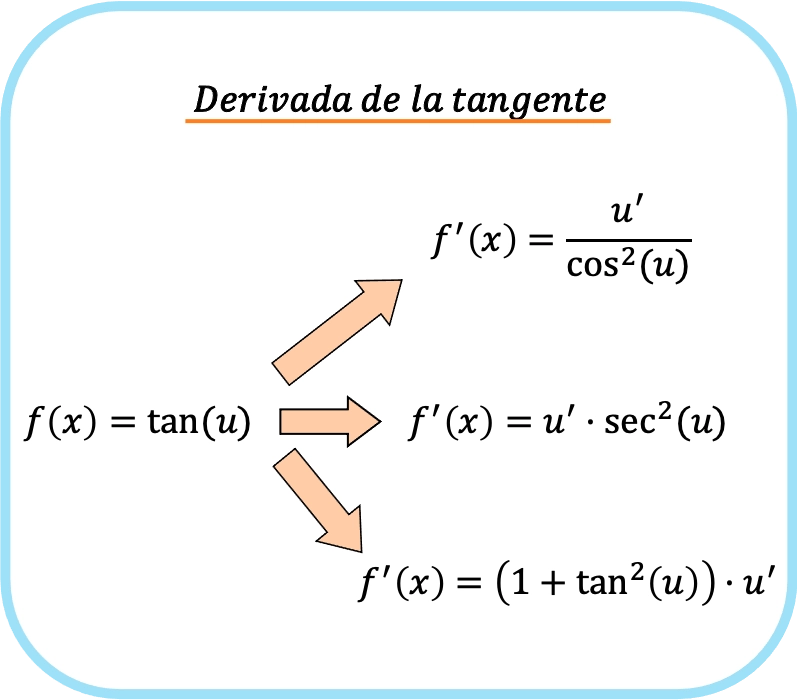
Öte yandan, teğet argümanında x’ten farklı bir fonksiyona sahip olduğumuzda (buna u diyelim), zincir kuralını uygulamamız gerekir. Dolayısıyla u’nun tanjantının türevi:

\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}

Kısaca teğet türev kuralı şu şekilde özetlenebilir:

teğet türev

Teğet türev örnekleri

Teğet türev formülü göz önüne alındığında, bu bölümde bu tür trigonometrik türevlerin birkaç örneğini çözeceğiz, böylece teğet fonksiyonunun nasıl türetileceğini anlayabilirsiniz.

Örnek 1: 2x’in tanjantının türevi

f(x)=\text{tan}(2x)

Teğetin türevini hesaplamak için yukarıda gördüğümüz üç formülden birini kullanabilirsiniz. Bu durumda kosinüs formülünü kullanacağız:

f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}

2x fonksiyonu doğrusal olduğundan türevi 2’dir. Yani 2x’in tanjantının türevi 2 bölü kosinüs 2x’in karesidir:

f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}

Örnek 2: x karenin tanjantının türevi

f(x)=\text{tan}(x^2)

Bu örnekte teğet argüman fonksiyonu bir x değil, türevi olan bir fonksiyondur. Bu, onu elde etmek için zincir kuralını uygulamamız gerektiği anlamına gelir.

f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}

x karenin türevi 2x olduğuna göre x 2’nin tanjantının türevi:

f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}

Örnek 3: Küpün teğetinin türevi

f(x)=\text{tan}^3(9x^2-4x)

Bu problemde bileşik bir fonksiyonumuz var, dolayısıyla teğetin türevini almak için zincir kuralını da kullanmamız gerekecek.

f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}

Ek olarak, teğet 3’ün kuvvetine yükseltilir; bu, teğetin türevi formülünü uygulamadan önce bir kuvvetin türevi formülünü kullanmanız gerektiği anlamına gelir:

\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}

Ters tanjantın türevi

Herhangi bir ters fonksiyon gibi, teğet fonksiyonun da bir tersi, arktanjant fonksiyonu vardır. Türetme formülü teğet formülüne benzemese de bazı durumlarda faydalı olabileceği için size gösteriyoruz.

Bir fonksiyonun ters tanjantının türevi, fonksiyonun türevinin bir artı söz konusu fonksiyonun karesine bölümüdür.

f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}

Örneğin 3x’in ters tanjantının türevi:

f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}

Teğetin türevine ilişkin çözülmüş alıştırmalar

Aşağıdaki teğet fonksiyonların türevini hesaplayın:

\text{A) } f(x)=\text{tan}(3x)

\text{B) } f(x)=\text{tan}(x^3-10x^2+8)

\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)

\text{D) } f(x)=\text{tan}\left(e^{2x}\right)

\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)

\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)

\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}

\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}

\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}

\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}

\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}

\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}

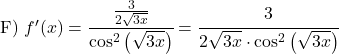
Teğetin türevinin kanıtı

Bunun uydurma bir ifade olmadığını doğrulayabilmeniz için, bu bölümde tanjantın matematiksel tanımını kullanarak tanjantın türevinin formülünü göstereceğiz.

Bunu yapmak için üç trigonometrik oranı birbirine bağlayan trigonometrik özdeşlikten başlayacağız:

\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}

Bir bölümün türevi için formülü kullanırsak türev şöyle olur:

\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'

\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}

\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}

Ancak temel trigonometrik özdeşliği kullanarak sinüsün karesi artı kosinüsün karesinin 1 olduğunu biliyoruz:

\text{sen}^2(x)+\text{cos}^2(x)=1

\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}

Böylece tanjantın türevinin ilk formülüne ulaştık. Ayrıca sekant kosinüsün çarpımsal tersi olduğundan ikinci ifade de türetilir:

\text{tan}'(x)=\text{sec}^2(x)

Son olarak, teğet türevin üçüncü kuralı, önceki adımdaki kesirin kesir toplamına dönüştürülmesiyle kanıtlanabilir:

\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}

\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}

\text{tan}'(x)=1+\text{tan}^2(x)

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top