Ortogonal matris - Mathority

Bu sayfada dik matrislerin ne olduğunu ve bir matrisin tersiyle olan ilişkilerini göreceksiniz. Ayrıca mükemmel bir şekilde anlamanız için birkaç örnek göreceksiniz. Ek olarak, herhangi bir dik matrisi kontrol eden formülü de öğretiyoruz; bu formülü kullanarak bir matrisi nasıl hızla bulacağınızı öğreneceksiniz. Ve son olarak, bu belirli matrislerin özelliklerini ve uygulamalarını ve ayrıca tipik bir çözülmüş sınav alıştırmasını bulacaksınız.

Dik matris nedir?

Ortogonal matrisin tanımı aşağıdaki gibidir:

Dik bir matris, devrik (veya devrik) ile çarpılarak birim matrise eşit olan kare bir gerçek sayı matrisidir. Yani aşağıdaki koşul karşılanmıştır:

$A\cdot A^t = A^t \cdot A =I$

Altın

$A$

ortogonal bir matristir ve

$A^t$

onun aktarılmış matrisini temsil eder.

Bu koşulun karşılanması için, dik bir matrisin sütunları ve satırları dik birim vektörler olmalıdır, yani ortonormal bir temel oluşturmalıdırlar. Bu nedenle bazı matematikçiler bunlara ortonormal matrisler de derler.

Dik bir matrisin tersi

Ortogonal matris kavramını açıklamanın başka bir yolu ters matristir, çünkü ortogonal bir matrisin transpoze (veya transpoze) matrisi onun tersine eşittir.

Bu teoremi tam olarak anlamak için bir matrisin nasıl ters çevrileceğini bilmeniz önemlidir. Bu bağlantıda bir matrisin tersinin ayrıntılı bir açıklamasını, tüm özelliklerini bulacaksınız ve hatta adım adım çözülmüş alıştırmalar bulacaksınız.

Bir ortogonal matrisin ters matrisinin, ortogonal matris koşulu ve ters matrislerin ana özelliği kullanılarak devriğine eşdeğer olduğu kolayca gösterilebilir:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Bu nedenle dik bir matris her zaman tersinir bir matris olacaktır, başka bir deyişle düzenli veya dejenere olmayan bir matris olacaktır.

Daha sonra, her şeyin kavramını anlamayı tamamlamak için birkaç dik matris örneği göreceğiz.

2×2 ortogonal matris örneği

Aşağıdaki matris 2×2 boyutunda dik bir matristir:

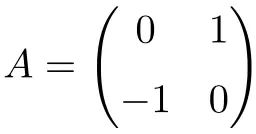
Çarpımı devrikle hesaplayarak dik olup olmadığını kontrol edebiliriz:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Sonuç Özdeş matrisi verdiğinden, A’nın dik bir matris olduğunu doğrularız.

3×3 ortogonal matris örneği

Aşağıdaki matris 3×3 boyutunda dik bir matristir:

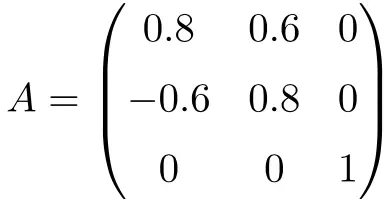
A matrisini devriğiyle çarparak bunun dik olduğunu gösterebiliriz:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Çözüm üniter matris olduğundan A’nın dik bir matris olduğunu gösteriyoruz.

2×2 dik matris bulma formülü

Daha sonra 2. mertebeden tüm dik matrislerin aynı modeli izlediğinin kanıtını göreceğiz.

2×2 boyutunda genel bir matris düşünün:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Bu matrisin dik olması için aşağıdaki matris denkleminin sağlanması gerekir:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Matris çarpımını çözerek aşağıdaki denklemleri elde ederiz:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Yakından bakarsanız, bu eşitlikler temel Pisagor trigonometrik ilişkisine çok benzer:

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Sonuç olarak, elde edilen denklemler (1) ve (3)’ü karşılayan terimler şunlardır:

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Ek olarak değerleri ikinci denklemde yerine koyarak iki açı arasındaki ilişkiyi elde ederiz:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Yani aşağıdaki iki koşuldan birinin karşılanması gerekir:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Sonuç olarak ortogonal matrisler aşağıdaki iki matristen birinin yapısına sahip olmalıdır:

2x2 boyutunun ortogonal matrisinin formülü

Altın

$\theta$

gerçek bir sayıdır.

Aslında, örnek olarak değeri verirsek

$\displaystyle\theta=\frac{\pi}{2}$

ve ilk yapıyı alıp “2×2 dik matris örneği” bölümünde dik olduğunu doğruladığımız matrisi elde edeceğiz:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Ortogonal Matris Özellikleri

Bu tür matrisin özellikleri şunlardır:

Dik bir matris asla tekil bir matris olamaz çünkü her zaman ters çevrilebilir. Bu anlamda bir dik matrisin tersi başka bir dik matristir.

Herhangi bir ortogonal matris köşegenleştirilebilir. Daha sonra dik matrislerin dik köşegenleştirilebilir olduğunu söylüyoruz.

Ortogonal bir matrisin tüm özdeğerleri veya özdeğerleri 1’e eşit bir modüle sahiptir.

Yalnızca gerçek sayılardan oluşan herhangi bir dik matris aynı zamanda normal bir matristir.

Karmaşık sayıların olduğu bir ortamda ortogonal matrisin analoğu üniter matristir.

Açıkçası, birim matrisi dik bir matristir.

n × n boyutunda ortogonal matrislerin kümesi ve matris çarpımının işlemi, ortogonal grup adı verilen bir grup oluşturur. Yani iki dik matrisin çarpımı başka bir dik matrise eşittir.

Ek olarak, dik bir matrisin devriğiyle çarpılmasının sonucu Kronecker deltası ile ifade edilebilir:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Son olarak dik bir matrisin determinantı her zaman +1 veya -1’dir.

$\displaystyle \text{det}(A)=\pm 1$

Ortogonal matrislerin çözülmüş alıştırması

Daha sonra dik matrislerle ilgili bir alıştırma çözeceğiz.

Aşağıdaki 3. dereceden kare matris verildiğinde, değerlerini bulun.
$a$

Ve

$b$

ortogonal yapmak için:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Matrisin ortogonalliğinin sağlanması için, matrisin devrik çarpımı Kimlik matrisine eşit olmalıdır. BU YÜZDEN:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

Matrisleri çarpıyoruz:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

Artık matrislerin sol üst köşesinden bir denklem elde edebiliriz çünkü o konumdaki elemanların eşleşmesi gerekir. Henüz:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

Denklemi çözüyoruz ve bilinmeyeni ortadan kaldırıyoruz:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Ancak pozitif çözüme uymayan denklemler de vardır, örneğin sağ üst köşedeki denklem. Yani yalnızca olumsuz çözüm mümkündür .

Öte yandan değişkeni hesaplamak için

$b$

örneğin ilk sütunun ikinci satırına yerleştirilen terimleri eşleştirebiliriz:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Değerini değiştirerek

$a$

denklemde:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Kısacası mümkün olan tek çözüm şudur:

$\displaystyle \bm{a=b =-2}$

Dolayısıyla bu değerlere karşılık gelen ortogonal matris şöyledir:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Ortogonal matrislerin uygulamaları

Genellikle çok basit bir forma sahip oldukları için öyle görünmese de, ortogonal matrisler matematikte, özellikle de lineer cebir alanında çok önemlidir.

Geometride ortogonal matrisler, gerçek vektör uzaylarındaki izometrik dönüşümleri (uzaklıkları ve açıları değiştirmeyen) temsil eder, bu nedenle bunlara ortogonal dönüşümler denir. Ayrıca bu dönüşümler, dikkate alınan vektör uzayının iç izomorfizmleridir. Bu dönüşümler dönmeler , aynasal yansımalar veya ters çevrilmeler olabilir.

Son olarak, bu tür matrisler, katı cisimlerin hareketinin incelenmesine olanak tanıdığı için fizikte de kullanılmaktadır. Hatta bazı alan teorilerinin formülasyonunda bile kullanılıyorlar.