Bir toplamın karesi (veya toplamın karesi)

Bu sayfada bir toplamın karesi formülünü, yani dikkate değer özdeşliği (a+b) ² bulacaksınız. Ayrıca kare toplamların örneklerini ve çözülmüş alıştırmalarını da görebileceksiniz. Üstelik bu olağanüstü üründe gizli olan geometrik özellikleri keşfedeceksiniz.

Bir toplamın karesi nedir?

Bir toplamın karesi dikkate değer kimliklerden (veya dikkate değer çarpımlardan) biridir, dolayısıyla iki kareli pozitif terimi olan bir binomun gücünü hızlı bir şekilde hesaplamanıza olanak tanıyan bir matematik kuralıdır.

Böylece bir toplamın karesi, iki farklı terimin toplanıp karesinden oluşur, yani bir toplamın karesinin cebirsel ifadesi (a+b) ^2’dir .

Bir toplamın karesi formülü

Bu dikkate değer özdeşlik türünün matematiksel tanımı göz önüne alındığında, şimdi bir toplamın karesinin formülünün ne olduğunu göreceğiz:

Yani bir toplamın karesi, birinci terimin karesi artı birinci terimin ikinci çarpımının iki katı artı ikinci terimin karesine eşittir.

Bu nedenle, bir kare toplamının çözülmesi için her toplamanın ikiye çıkarılması yeterli değildir, ayrıca iki toplamanın birlikte ve 2 ile çarpılması gerekir.

Bunu hatırlamak önemlidir, çünkü kareleri eklerken çok sık yapılan bir hata, iki terim arasındaki çarpımı unutup yalnızca kareleri hesaplamaktır:

Hiçbir terimi formülün dışında bırakmamayı unutmayın!

Öte yandan, kare çıkarma formülünün (veya çıkarma işleminin karesinin) az önce gördüğümüz formüle çok benzediğini ancak sonucu tamamen değiştiren bir farkı olduğunu unutmayın. Bunun neye benzediğinden emin değilseniz, kare çıkarma formülünün ne olduğunu ve nasıl uygulandığını buradan kontrol edebilirsiniz.

Toplam kareler örnekleri

Bir toplamın karesinin nasıl alınacağını görebilmeniz için burada birkaç pratik örnek verilmiştir:

örnek 1

Formülü uygulayarak aşağıdaki toplamın karesini hesaplayın:

$(x+5)^2$

Kare toplamın formülü şöyledir:

$(a+b)^2=a^2+2ab+b^2$

İlk önce parametreleri tanımlamalıyız

$a$

$b$

formülü. Bu durumda,

$a$

temsil etmek

$x$

çiftin ve

$b$

5 numaraya karşılık gelir:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Artık değerlerini bildiğimize göre

$a$

$b,$

Toplamın karesinin sonucunu bulmak için formülü uygulayabiliriz:

Örnek 2

Bir toplamın karesi için aşağıdaki ifadeyi çözün:

$(3x+4)^2$

Bir toplamın karesi formülü şöyledir:

$(a+b)^2=a^2+2ab+b^2$

Yani bu problemde

$a$

tek terimli

$3x$

Öte yandan,

$b$

bağımsız terim 4’tür:

$\begin{array}{c} a=3x \\[2ex] b=4 \end{array}$

Son olarak değerlerini belirledikten sonra

$a$

$b$

dikkate değer çarpımı çözmek için kare toplamı formülünü uyguluyoruz:

$\begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}$

Bir toplamın karesi formülünün kanıtı

Daha sonra az önce gördüğümüz formülü bir toplamın karesinden çıkaracağız, böylece nereden geldiğini anlayabilirsiniz.

2’ye yükseltilmiş pozitif bir binomdan başlayarak:

$(a+b)^2$

Yukarıdaki güç açıkça faktöre eşdeğerdir

$(a+b)$

kendisi ile çarpılır:

$(a+b)^2=(a+b)\cdot (a+b)$

Bu nedenle, dağılma özelliğini kullanarak iki parantezi çarpıyoruz:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Son olarak, ortaya çıkan terimlerden benzer olanları gruplandırıyoruz:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Ve formülün polinom ifadesine zaten ulaştık, dolayısıyla kanıtlandı:

$(a+b)^2= a^2+2ab+b^2$

İnanması zor olsa da, toplam formülünün karesi aynı zamanda ikinci dereceden polinomları çarpanlara ayırmada da işe yarar. Ne olduğunu bilmiyorsanız, polinom çarpanlarına ayırma, matematikte bir polinomun ifadesini basitleştirmek için sıklıkla kullanılan bir prosedürdür. Yukarıdaki bağlantıya tıklayarak bunun nasıl yapıldığını öğrenin.

Bir toplamın karesinin geometrik yorumu

Şu ana kadar bir toplamın karesinin matematiksel olarak nasıl hesaplandığını gördük ancak bu dikkat çekici çarpım geometrik olarak da yorumlanabiliyor.

Kenarları ölçülen aşağıdaki kareye bakın

$a+b:$

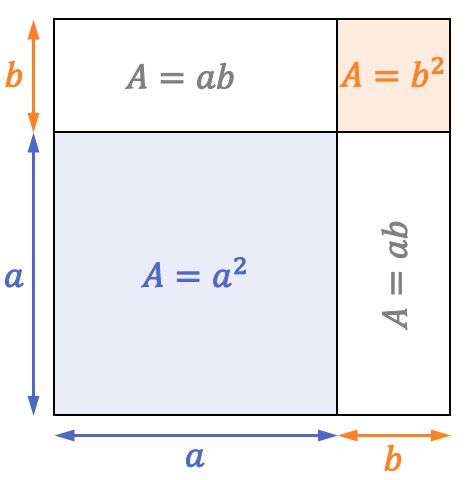
Bir karenin alanı, bir kenarının uzunluğunun karesine eşittir. Bu nedenle önceki karenin kenarı olduğundan

$a+b,$

alanı (veya yüzeyi) eşittir

$(a+b)^2.$

Kare gösteriminde görebileceğiniz gibi, alanı

$a^2,$

iki alanı olan dikdörtgenler

$ab,$

ve başka bir yüzey karesi

$b^2.$

Dolayısıyla karenin toplamına ilişkin formül geometrik açıdan da yerine getirilir:

$(a+b)^2=a^2+2ab+b^2$

Bir toplamın karesi ile ilgili çözülmüş problemler

Ardından, pratik yapabilmeniz ve böylece kavramı anlamayı tamamlayabilmeniz için sizi adım adım çözülmüş kareler toplamları alıştırmalarıyla baş başa bırakıyoruz. Tüm sorularınızı yorum olarak bize yazabilirsiniz, cevaplamaktan mutluluk duyarız. 💭💭💭

1. Egzersiz

Aşağıdaki toplamların karesini belirleyin:

$\text{A)} \ (x+3)^2$

$\text{B)} \ (2+6x)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

Çözüme bakın

Sorunun tüm önemli özelliklerini çözmek için toplamın karesi formülünü uygulamak yeterlidir:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Alıştırma 2

Aşağıdaki iki terimin toplam karelerini aşağıdaki formülü uygulayarak çözün:

$\text{A)} \ \left(4x^2+2y^3\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}+\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

Çözüme bakın

Sorunun tüm önemli ürünlerini hesaplamak için, kare toplamı formülünü kullanmanız gerekir:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

Bölüm B)’de, eğer bir kökün karesi alınırsa basitleştirildiğini hatırlamanız gerekir:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}$

Son kare toplamının monomlarının kesirli katsayıları vardır, dolayısıyla bunu çözmek için kesirlerin özelliklerini de kullanmamız gerekir:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

Alıştırma 3

Bir toplamın karesi formülünü hesap makinesini kullanmadan uygulayarak aşağıdaki gücü bulun:

$17^2$

Çözüme bakın

Öncelikle on yedi sayısını 10 artı 7’nin toplamına ayırabiliriz:

$17^2=(10+7)^2$

Böylece gücü kare toplamına dönüştürdük. Bu nedenle artık ilgili formülü uygulayabiliriz:

$\begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}$

Kısaca, potansiyelleşmenin sonucu:

$17^2=\bm{289}$

Bu alıştırmada gördüğünüz gibi, toplam kare formülü, hesap makinesi kullanmadan büyük sayıların kuvvetlerini hesaplamak için de kullanışlıdır.

3 terimin toplamının karesi

Bazen eklenen üç terimin (a+b+c) ^2’nin karesini çözmemiz gerektiğini görebiliriz. Mantıksal olarak bu durumlarda açıkladığımız formülü kullanamayız çünkü parantezlerin içinde binom yerine üç terimli vardır. Bu nedenle farklı bir formül kullanılması gerekmektedir.

3 terimin toplamının karesi formülü aşağıdaki gibidir:

$\definecolor{blauquadreejemplo}{HTML}{ff5733} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=blauquadreejemplo, boxrule=1.2pt, boxsep=2.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2.5mm}{-2.5mm}{0mm}{blauquadreejemplo!20!white,} ]}]{equation*} (a+b+c)^2 = a^2+2a(b+c)+b^2+2bc+c^2 \end{empheq}$

Bu formülün nasıl uygulandığını bir örnek üzerinden görelim:

$\begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}$

Gördüğünüz gibi formüle bir öğe eklemek sonucu çok daha karmaşık hale getiriyor.

Bir toplamın karesi nedir?

Bir toplamın karesi formülü

Toplam kareler örnekleri

örnek 1

Örnek 2

Bir toplamın karesi formülünün kanıtı

Bir toplamın karesinin geometrik yorumu

Bir toplamın karesi ile ilgili çözülmüş problemler

1. Egzersiz

Alıştırma 2

Alıştırma 3

3 terimin toplamının karesi

Yorum bırakın Yanıtı iptal et