▷ Kosinüsün türevi (formül ve çözülmüş alıştırmalar)

Burada kosinüs fonksiyonunun (formül) nasıl türetileceğini keşfedeceksiniz. Kosinüs fonksiyonlarının türevlerinin örneklerini görebileceksiniz ve adım adım alıştırmalarla pratik yapabileceksiniz. Ayrıca size kosinüsün ikinci türevinin ve hatta ters kosinüsün türevinin ne olduğunu gösteren formülün kanıtını da gösteriyoruz.

Kosinüsün türevi nedir?

Kosinüs fonksiyonunun türevi, işareti değiştirilmiş sinüs fonksiyonudur. Başka bir deyişle, kosinüs x’in türevi eksi sinüs x’e eşittir.

$f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)$

Kosinüs argümanında bir fonksiyon varsa, kosinüsün türevi eksi o fonksiyonun sinüsü çarpı fonksiyonun türevinin çarpımıdır.

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

İkinci formül birinci formüle eşdeğerdir ancak zincir kuralını uygular. Yani özetle kosinüsün türevinin formülü aşağıdaki gibidir:

Kosinüs türevi örnekleri

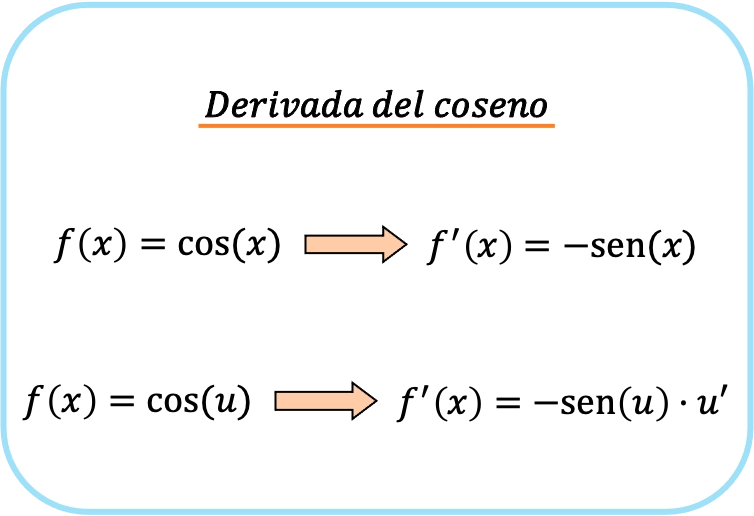
Artık kosinüs formülünün ne olduğunu bildiğimize göre, bu tür trigonometrik türevlerin birkaç örneğini açıklayacağız, böylece kosinüs fonksiyonunun nasıl türetileceği konusunda hiçbir şüpheniz kalmaz.

Örnek 1: 2x kosinüsünün türevi

$f(x)=\text{cos}(2x)$

Kosinüs argümanında tek bir x’imiz yok, bunun yerine daha karmaşık bir fonksiyonumuz var. Bu nedenle kosinüsü elde etmek için aşağıdaki formülü kullanmamız gerekir:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

2x’in türevi 2 olduğundan, 2x’in kosinüsünün türevi eksi 2x’in sinüsü çarpı 2 olacaktır.

$f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)$

Örnek 2: Kosinüs x karenin türevi

$f(x)=\text{cos}(x^2)$

Önceki örnekte olduğu gibi, kosinüs argümanında x’ten farklı bir fonksiyona sahibiz, dolayısıyla kosinüsü türetmek için zincir kuralını kullanacağız:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

O zaman x ^2’nin türevi 2x’tir, dolayısıyla x’in kosinüsünün 2’ye yükseltilmiş türevi şöyle olur:

$f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x$

Örnek 3: Küp kosinüsün türevi

$f(x)=\text{cos}^3(2x^6-5x^3)$

Bu örnekteki kosinüs fonksiyonu başka bir fonksiyondan oluştuğundan türevi çözmek için aşağıdaki formülü uygulamamız gerekir:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Böylece formülü uygulayarak fonksiyonun türevine ulaşırız:

$\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}$

➤ Bu fonksiyonun türevini almak için potansiyel fonksiyonun türevi formülünü de kullanmalısınız.

Kosinüsün ikinci türevi

Daha sonra trigonometrik fonksiyonların özellikleri sayesinde sinüsün ikinci türevinin kolayca hesaplanabileceğini göreceğiz.

➤ Not: Aşağıdakileri anlamak için sinüsün türevinin ne olduğunu bilmeniz gerekir .

Kosinüs x’in ikinci türevi eksi kosinüs x’tir. Bu garip görünebilir ama matematiksel olarak böyledir. Aslında sinüsün türevi kosinüstür ve bu nedenle x’in kosinüsünün iki kez türevi alınarak kosinüs yeniden elde edilir, ancak işaret değiştirilmiş.

$\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}$

Bu özellik, kosinüs argümanı x değilse değişir, çünkü bu durumda zincir kuralının terimini sürükleriz:

$\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}$

Ters kosinüsün türevi

Tüm trigonometrik fonksiyonların ters bir fonksiyonu vardır ve bu nedenle kosinüs fonksiyonu da ters çevrilebilir. Benzer şekilde, ters kosinüs de türevlenebilirdir.

Bir fonksiyonun ters kosinüsünün türevi eksi fonksiyonun türevinin birin karekökü eksi söz konusu fonksiyonun karesine bölümüdür.

$f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Ters kosinüsün aynı zamanda arkkosinüs olarak da adlandırıldığını unutmayın.

Örneğin 3x’in ters kosinüsünün türevi:

$f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}$

Kosinüs türevine ilişkin çözülmüş alıştırmalar

Aşağıdaki kosinüs fonksiyonlarının türevini hesaplayın:

$\text{A) } f(x)=\text{cos}(4x)$

$\text{B) } f(x)=\text{cos}(2x^3-5x+1)$

$\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)$

$\text{D) } f(x)=\text{cos}^5(x^2+3x)$

$\text{E) } f(x)=\text{cos}\left(e^{5x}\right)$

$\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)$

Çözümü görün

$\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)$

$\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)$

$\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)$

$\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)$

$\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}$

$\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}$

Kosinüs türevinin kanıtı

Son olarak, kosinüs x’in türevinin formülünü matematiksel olarak göstereceğiz. Bunu yapmak için aşağıdaki limite karşılık gelen türev tanımını kullanacağız:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Kosinüsü kanıtlayacağız, dolayısıyla fonksiyon cos(x) olur:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x+h)-\text{cos}(x)}{h}$

Bu limiti ikame yoluyla çözemeyiz çünkü sonuçta belirsizlikle sonuçlanırız. Ancak bir toplamın kosinüsünü aşağıdaki trigonometrik özdeşliği uygulayarak başka bir şekilde ifade edebiliriz:

$\text{cos}(a+b)=\text{cos}(a)\text{cos}(b)-\text{sen}(a)\text{sen}(b)$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\text{cos}(h)-\text{sen}(x)\text{sen}(h)-\text{cos}(x)}{h}$

Bir sonraki adım, kesri iki kesire ayırmak ve kosinüsün ortak faktörünü almaktır:

$\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]$

Bir çıkarma işleminin limiti, limitlerin çıkarılmasına eşittir, dolayısıyla:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\lim_{h \to 0}\frac{\text{sen}(x)\text{sen}(h)}{h}$

X’in kosinüsü ve x’in sinüsü h’ye bağlı değildir, dolayısıyla bunları sınırların dışına çıkarabiliriz:

$\displaystyle f'(x)=\text{cos}(x)\lim_{h \to 0}\frac{\text{cos}(h)-1}{h}-\text{sen}(x)\lim_{h \to 0}\frac{\text{sen}(h)}{h}$

Limitlerin sonsuz küçük eşdeğerlere göre hesaplanmasını kullanarak, ilk limitin 0 ve ikinci limitin 1 olduğu sonucuna varırız. Dolayısıyla:

$\displaystyle f'(x)=\text{cos}(x)\cdot 0-\text{sen}(x)\cdot 1$

$\displaystyle f'(x)=-\text{sen}(x)$

Ve kosinüs fonksiyonunun türevinin formülüne zaten ulaştık, böylece eşitlik kanıtlandı.

Kosinüsün türevi nedir?

Kosinüs türevi örnekleri

Örnek 1: 2x kosinüsünün türevi

Örnek 2: Kosinüs x karenin türevi

Örnek 3: Küp kosinüsün türevi

Kosinüsün ikinci türevi

Ters kosinüsün türevi

Kosinüs türevine ilişkin çözülmüş alıştırmalar

Kosinüs türevinin kanıtı

Yorum bırakın Yanıtı iptal et