Faktör teoremi - Mathority

Bu sayfada faktör teoreminin ne olduğunu açıklıyoruz. Ek olarak, faktör teoreminin ne için kullanıldığını da gösteriyoruz: polinomların bölünebilirliği, kökleri bulma, polinomları çarpanlara ayırma, vb. Son olarak faktör teoremi üzerine adım adım alıştırmalar yapabileceksiniz.

Faktör teoremi nedir?

Matematikte faktör teoremi , bir P(x) polinomunun (xa) formundaki başka bir polinomla ancak ve ancak P(a)=0 olması durumunda bölünebileceğini söyler.

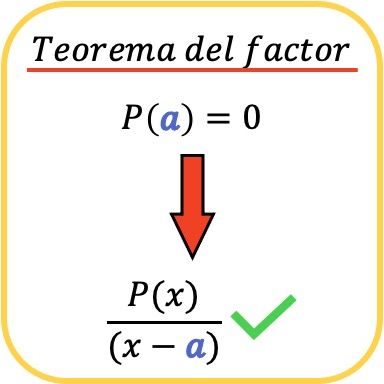
Benzer şekilde, faktör teoreminin bir sonucu olarak, eğer bir P(x) polinomu (x−a) terimine bölünebiliyorsa, bu, a değerinin P( x) polinomunun bir kökü (veya sıfırı) olduğu anlamına gelir. ).

Bir polinomun diğerine bölünebilir olması, iki polinom arasındaki bölümün geri kalanının (veya kalanının) sıfıra eşit olduğu anlamına gelir. Bu kavramı tam olarak hatırlamıyorsanız, aşağıdaki bağlantıdapolinomların bölünmesiyle ilgili örnekleri görebilirsiniz, burada ayrıca polinomların nasıl bölüneceğinin açıklamasını ve adım adım çözülmüş alıştırmaları bulacaksınız.

Faktör Teoremi Örnekleri

Artık faktör teoreminin matematiksel tanımını bildiğimize göre, bunun nasıl uygulandığını görmek için birkaç örneğe bakalım.

örnek 1

Faktör teoreminin bir uygulaması, belirli bir polinomun bir binoma bölünebilir olup olmadığını bulmaktır. Bunun faktör teoremi ile nasıl yapıldığına dair bir örnek görelim:

P(x) polinomunun binom Q(x)’e bölünebilir olup olmadığını belirleyin; her ikisi de:

$P(x)=x^2-4x+3 \qquad \qquad Q(x)=x-1$

İlk olarak, bölen polinomu Q(x), (xa) türünde bir polinomdur, dolayısıyla sorunu çözmek için faktör teoremini uygulayabiliriz.

Dolayısıyla, P(x)’in Q(x)’e bölünüp bölünemeyeceğini kontrol etmek için x=1 için P(x) polinomunun sayısal değerini hesaplamamız gerekir, çünkü 1, işareti değiştirilmiş olarak bölen polinomun bağımsız terimidir. :

$\begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}$

P(x) polinomunun x = 1’deki sayısal değeri sıfır verir, yani faktör teoremine göre P(x), Q(x)’e bölünebilir, başka bir deyişle, her ikisine bölünmenin geri kalanı boş olacaktır.

2 polinomu Ruffini teoremine bölerek bölünebilme koşulunun sağlandığını doğrulayabiliriz:

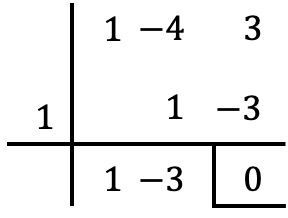
faktör teoremi çözülmüş alıştırmalar pdf çevrimiçi

Bu örnekte görebileceğiniz gibi, faktör teoremi kalan (veya kalan) teoreminin özel bir durumudur. Geri kalan teoreminin ne olduğunu açıklayan bu makaleyi size bırakıyorum, ayrıca onunla çözülmüş örnekler ve alıştırmalar da bulacaksınız. Dahası, kalan teoremi ile faktör teoremi arasındaki farkın ne olduğunu görebileceksiniz.

Örnek 2

Faktör teoremi bir polinomun köklerini (veya sıfırlarını) bulmak için de kullanılabilir. Ancak açıkçası bu tür bir problemi anlamak için bir polinomun köklerinin ne olduğunu bilmeniz gerekir. Eğer hala bu kavramı anlamadıysanız detaylı bir şekilde anlatılan bağlantılı sayfaya göz atabilirsiniz.

Bir polinomun kökünü bulmak için faktör teoreminin nasıl uygulandığını bir örnekle görelim:

P(x) polinomu verildiğinde, köklerinden birinin x=2 olup olmadığını hesaplayın:

$P(x)=x^3-3x^2+5x-6$

Faktör teoremi uygulandığında, x=2 terimi yalnızca P(x) polinomunun bir kökü olacaktır, eğer x=2 için P(x)’in sayısal değeri sıfırsa. O halde bu sayısal değeri bulmamız gerekiyor:

$\begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}$

Aslında, P(x) polinomunun sayısal değeri x=2’de sıfırdır, dolayısıyla faktör teoremi sayesinde x=2’nin P(x) polinomunun bir kökü olduğunu doğrulayabiliriz.

Faktör Teoremini Kullanarak Polinomları Faktoring Etme

Faktör teoreminin başka bir uygulaması polinomların çarpanlarına ayrılmasıdır . Ne olduğunu bilmiyorsanız, bir polinomu çarpanlara ayırmak, bir polinomun ifadesini faktörlerin çarpımına dönüştürmek anlamına gelir, yani bir polinomu çarpanlara ayırmak onun cebirsel ifadesini basitleştirir.

Dolayısıyla, faktöriyel teoremi, eğer bir P(x) polinomu, belirli bir a değeri için P(a)=0’ı sağlıyorsa, söz konusu polinomun ifadesinin P(x)=(xa)·Q( çarpımına çarpanlara ayrılabileceğini belirler. x), burada Q(x), P(x) polinomunun (xa)’ya bölünmesinden elde edilen polinomdur.

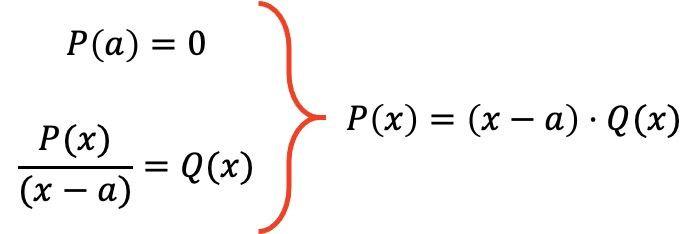
Örnek olarak, faktöriyel teoremi kullanarak aşağıdaki polinomu çarpanlarına ayıracağız:

$P(x)=x^3+2x^2+4x+8$

Önceki polinomdan, x=-2’nin köklerinden biri olduğunu biliyoruz, çünkü x=-2 için polinomun sayısal değeri sıfıra eşittir:

$\begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}$

Bu nedenle, Ruffini kuralıyla P(x) polinomunu x tarafından oluşturulan binom ile bu kök değişen işaret, yani (x+2) faktörü arasında bölüyoruz:

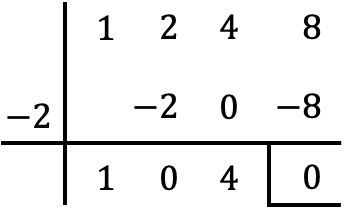
Yani polinom bölümünün bölümü şöyledir:

$\cfrac{P(x)}{x+2} =x^2+4$

Ve son olarak, faktör teoreminden, P(x) polinomunu, (x+2) faktörünün önceki bölmede elde edilen bölümle çarpımı şeklinde ifade edebiliriz:

$P(x) = (x+2) \cdot (x^2+4)$

Böylece P(x) polinomunu kısmen çarpanlara ayırdık. Bir polinomun tamamen çarpanlara ayrılması için daha uzun bir prosedürün uygulanması gerekir. Ruffini polinomlarının nasıl çarpanlara ayrılacağını adım adım öğrettiğimiz bir rehber hazırladık, ayrıca bu yazımızda tüm çarpanlara ayırma türlerini anlattık ve çözümlü alıştırmalarla pratik yapabileceksiniz. Bir polinomun kümeden nasıl çarpanlara ayrılacağını öğrenmek için bağlantıya tıklayın.

Çözülmüş Faktör Teoremi Problemleri

Daha sonra pratik yapabilmeniz ve bu teoremi anlayıp anlamadığınızı kontrol edebilmeniz için faktör teoremi üzerinde adım adım çözülen birkaç alıştırma hazırladık. Bunları kendiniz yapmayı denemenizi ve ardından çözümü doğru anlayıp anlamadığınızı görmenizi öneririz. Ayrıca sorularınızı aşağıya yorum olarak bize bırakabileceğinizi de unutmayın! ❓❓💬💬

1. Egzersiz

P(x) polinomunun binom Q(x)’e bölünebilir olup olmadığını bulmak için faktöriyel teoremini kullanın ve eğer öyleyse, polinomun bir kökünü bulun ve çarpanlarına ayırın.

$P(x)=2x^3-4x^2+x-7 \qquad \qquad Q(x)=x-3$

Çözüme bakın

Bu durumda polinom böleni Q(x), yalnızca bir x ve bağımsız bir terimden oluşan bir binomdur. Dolayısıyla, P(x) polinomunun diğer Q(x) polinomuna faktöriyel teoremi ile bölünebileceğini göstermek için, P(x) polinomunun sayısal değerini bölen polinomun değiştirilmiş işaretinin bağımsız teriminde değerlendirmeliyiz, yani x=3’te:

$\begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}$

P(x) polinomunun x=3’teki sayısal değeri 14’e eşittir, yani sıfırdan farklıdır. Dolayısıyla, faktör teoremine göre P(x), Q(x)’e bölünemez çünkü bölümün geri kalanı sıfır değildir.

Alıştırma 2

Faktöriyel teoremi kullanarak, P(x) polinomunun binom Q(x)’e bölünebilir olup olmadığını bulun ve eğer öyleyse, P(x) polinomunun bir kökünü bulun ve bunu çarpanlara ayırın.

$P(x)=x^3+5x^2+3x-1 \qquad \qquad Q(x)=x+1$

Çözüme bakın

Bu durumda polinom böleni Q(x), yalnızca bir x ve bağımsız bir terimden oluşan bir binomdur, bu nedenle faktöriyel teoremini uygulayabiliriz.

Ve P(x) polinomunun Q(x) polinomuna bölünüp bölünemeyeceğini kontrol etmek için, Q(x) değişen işaretinin bağımsız terimi için polinom P(x)’in sayısal değerini bulmamız gerekir; yani x=-1’de:

$\begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}$

Bu problemde, x=-1’deki polinomun sayısal değeri sıfırdır, dolayısıyla P(x), Q(x)’e bölünebilir.

Daha sonra faktöriyel teoremi kullanarak x=-1’in P(x) polinomunun bir kökü olduğu sonucunu çıkarabiliriz, çünkü P(x)’in x=-1’deki sayısal değeri sıfırdır.

Dolayısıyla, x=-1, P(x) polinomunun bir kökü olduğundan, bunu çarpanlarına ayırmak için onu x+1’e bölmeniz yeterlidir. Bunun için Ruffini yöntemini kullanacağız:

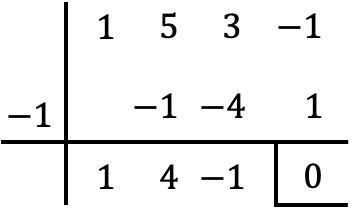
Yani operasyonun sonucu:

$x^2+4x-1$

Bu nedenle P(x) polinomunu aşağıdaki gibi çarpanlara ayırabiliriz:

$P(x) = (x+1) \cdot (x^2+4x-1)$

Alıştırma 3

Faktöriyel teoremi kullanarak, P(x) polinomunun binom Q(x)’e bölünebilir olup olmadığını bulun ve eğer öyleyse, P(x) polinomunun bir kökünü bulun ve onu çarpanlara ayırın.

$P(x)=x^3+5x^2+4x-6 \qquad \qquad Q(x)=x+3$

çözümü gör

Bu durumda Q(x)’i bölen polinom, yalnızca bir x ve bağımsız bir terimden oluşan bir binom olduğundan, faktör teoremini kullanabiliriz.

Ve P(x) polinomunun Q(x) polinomuna bölünebilir olup olmadığını kontrol etmek için, Q(x) değişen işaretinin bağımsız terimi için polinom P(x)’in sayısal değerini belirlememiz gerekir; yani x =-3’te:

$\begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}$

Bu durumda, x=-3’teki polinomun sayısal değeri sıfırdır, dolayısıyla P(x) aslında Q(x)’e bölünebilir.

Bu nedenle, faktöriyel teoremden, P(-3) sıfıra eşit olduğundan, x=-3’ün P(x) polinomunun bir kökü olduğu sonucunu çıkarıyoruz.

Dolayısıyla x=-3, P(x) polinomunun bir kökü olduğundan, bunu çarpanlarına ayırmak için onu x+3’e bölmemiz gerekir. Bunun için Ruffini kuralını kullanacağız:

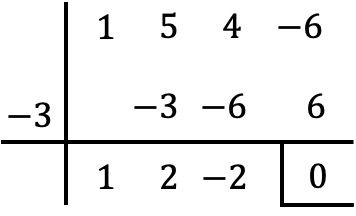
faktör teoremi faktör ruffini tarafından

Yani bölme işleminin sonucu:

$x^2+2x-2$

Dolayısıyla P(x) polinomunu aşağıdaki şekilde çarpanlara ayırabiliriz:

$P(x) = (x+3) \cdot (x^2+2x-2)$

Faktör teoremi hakkında ne düşünüyorsunuz? Cebirde yararlı olduğunu düşünüyor musunuz? Sizi yorumlarda okuyoruz!
👀⬇⬇⬇👀