Bu sayfa kesinlikle Hessian matrisinin var olan en eksiksiz açıklamasıdır. Burada Hessian matrisi kavramı açıklanıyor, örneklerle nasıl hesaplanacağı ve hatta uygulanabilecek birkaç çözülmüş alıştırma var. Ek olarak, çok değişkenli bir fonksiyonun maksimum ve minimum değerlerinin nasıl hesaplandığını ve bunun içbükey mi yoksa dışbükey bir fonksiyon mu olduğunu öğrenebileceksiniz. Ve son olarak Hessian matrisi yardımcı programlarını ve uygulamalarını da bulacaksınız.
Hessian matrisi nedir?
Hessian (veya Hessian) matrisinin tanımı aşağıdaki gibidir:
Hessian matrisi, n değişkenli bir fonksiyonun kısmi ikinci türevlerinden oluşan n × n boyutunda bir kare matristir.
Bu matris aynı zamanda Hessian olarak da bilinir, hatta bazı matematik kitaplarında Diskriminant olarak da adlandırılır. Ancak bunu adlandırmanın en yaygın yolu Hessian matrisidir.
Dolayısıyla Hessian matrisinin formülü aşağıdaki gibidir:

Bu nedenle Hessian matrisi her zaman boyutu fonksiyondaki değişken sayısına eşit olan bir kare matris olacaktır. Örneğin, fonksiyonun 3 değişkeni varsa Hessian matrisinin boyutu 3×3 olacaktır.
Ek olarak, Schwarz teoremi (veya Clairaut teoremi), türev alma sırasının önemli olmadığını, yani değişkene göre kısmen ilk önce türetildiğini söyler.
![]()
o zaman değişkene göre
![]()
açısından kısmen farklılaşma anlamına gelir
![]()
o zaman saygı duy
![]()
.
![]()
Dolayısıyla Hessian matrisi simetrik bir matristir veya başka bir deyişle ekseni asal köşegeni olan bir simetriye sahiptir.
İlginç bir şekilde Hessian matrisi, adını lineer cebir alanına çok önemli katkılarda bulunan 19. yüzyıl Alman matematikçisi Ludwig Otto Hesse’den almıştır.
Hessian matrisini hesaplama örneği
2 × 2 boyutlu bir Hessian matrisinin nasıl bulunacağına dair bir örnek görelim:
- Aşağıdaki fonksiyonun (1,0) noktasındaki Hessian matrisini hesaplayın:
![]()
Öncelikle birinci dereceden kısmi türevleri hesaplamamız gerekir:
![]()
![]()
İlk türevleri zaten bildiğimizde, tüm ikinci dereceden kısmi türevleri hesaplarız:
![]()
![]()
![]()
Bu nedenle artık Hessian matrisini 2 × 2 matris formülünden bulabiliriz:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-926f350fe0ac3184ec0b563b57fd6041_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b7f3d45918645a5b6019896ed45eda75_l3.png)
Böylece (1,0) noktasında değerlendirilen Hessian matrisi şöyle olacaktır:
![Rendered by QuickLaTeX.com \displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdccfc61f7befe6c75f66c8a4658f3e6_l3.png)
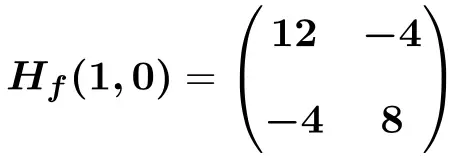
Hessian matrislerinin çözülmüş problemleri
1. Egzersiz
(1,1) noktasında 2 değişkenli aşağıdaki fonksiyonun Hessian matrisini hesaplayın:
![]()
Öncelikle fonksiyonun birinci dereceden kısmi türevlerini bulmamız gerekiyor:
![]()
![]()
İlk türevleri zaten hesapladıktan sonra, tüm ikinci dereceden kısmi türevleri çözmeye devam ederiz:
![]()
![]()
![]()
Böylece Hessian matrisi şu şekilde tanımlanır:
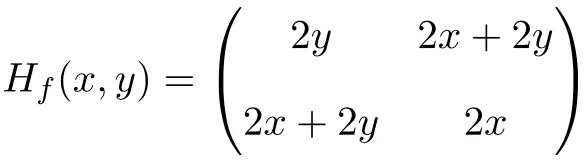
Son olarak geriye kalan tek şey Hessian matrisini (1,1) noktasında değerlendirmektir:
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5353c0229942269e07455047284f92b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf00fccdb37a19388e76b5a84a408d02_l3.png)
Alıştırma 2
İki değişkenli aşağıdaki fonksiyonun (1,1) noktasındaki Hessian’ı hesaplayın:
![]()
Öncelikle fonksiyonun birinci dereceden kısmi türevlerini hesaplamamız gerekir:
![]()
![]()
İlk türevleri elde ettikten sonra fonksiyonun ikinci dereceden kısmi türevlerini hesaplarız:
![]()
![]()
![]()
Dolayısıyla fonksiyonun Hessian matrisi 2×2 boyutunda bir kare matristir:
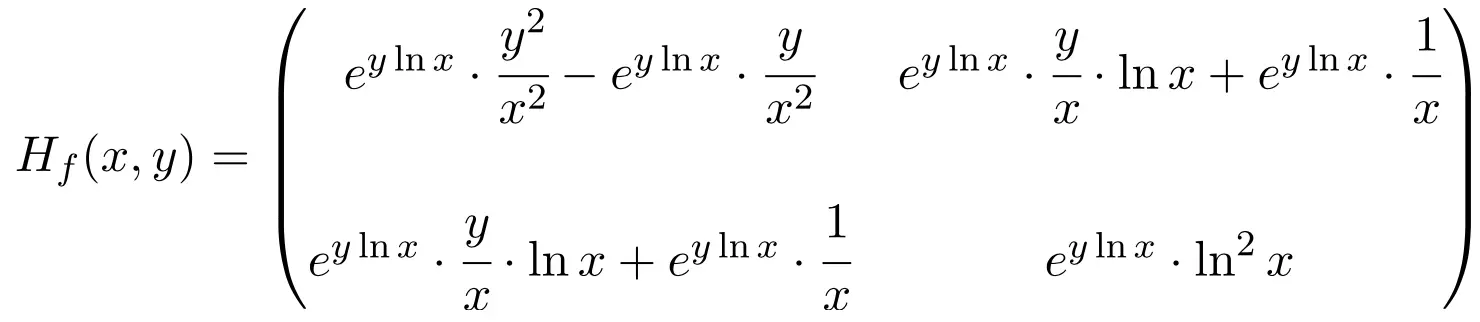
Son olarak geriye kalan tek şey Hessian matrisini (1,1) noktasında değerlendirmektir:
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c316cc61e6d007e5d034274e0f494520_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e456b856c722a140d73ade63f13ec9f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-929fbf6e7f0f90110d11d4ccd51fd51a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce780ddb8c09515afccfb2da2d842584_l3.png)
Alıştırma 3
Bu noktada Hessian matrisini bulun
![]()
3 değişkenli aşağıdaki fonksiyondan:
![]()
Öncelikle fonksiyonun birinci dereceden kısmi türevlerini hesaplıyoruz:
![]()
![]()
![]()
İlk türevleri elde ettikten sonra fonksiyonun ikinci dereceden kısmi türevlerini hesaplarız:
![]()
![]()
![]()
![]()
![]()
![]()
Böylece fonksiyonun Hessian matrisi 3×3 boyutunda bir kare matris olur:
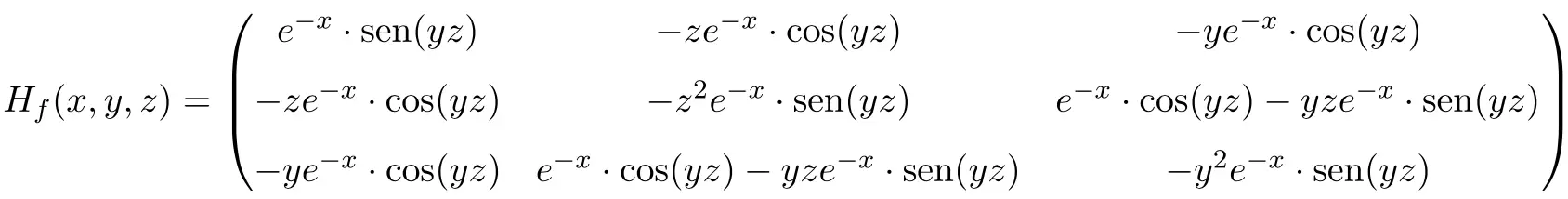
Son olarak değişkenleri ilgili noktadaki değerleriyle değiştiriyoruz.
![]()
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e198192f67babd81228caa53b66e8a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ce9c6b4cfcddfb0c2eb51db1189c653_l3.png)
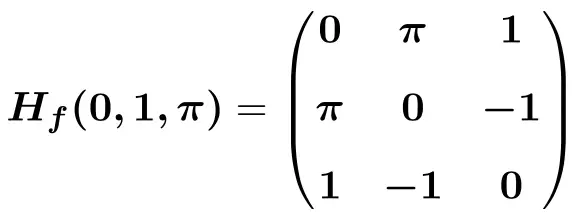
Alıştırma 4
4 değişkenli aşağıdaki fonksiyonun (2,-1,1,-1) noktasındaki Hessian matrisini belirleyin:
![]()
İlk adım, fonksiyonun birinci dereceden kısmi türevlerini bulmaktır:
![]()
![]()
![]()
![]()
Şimdi fonksiyonun ikinci dereceden kısmi türevlerini çözüyoruz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Böylece tüm kısmi türevlerin çözülmesiyle elde edilen 4×4 Hessian matrisinin ifadesi aşağıdaki gibidir:
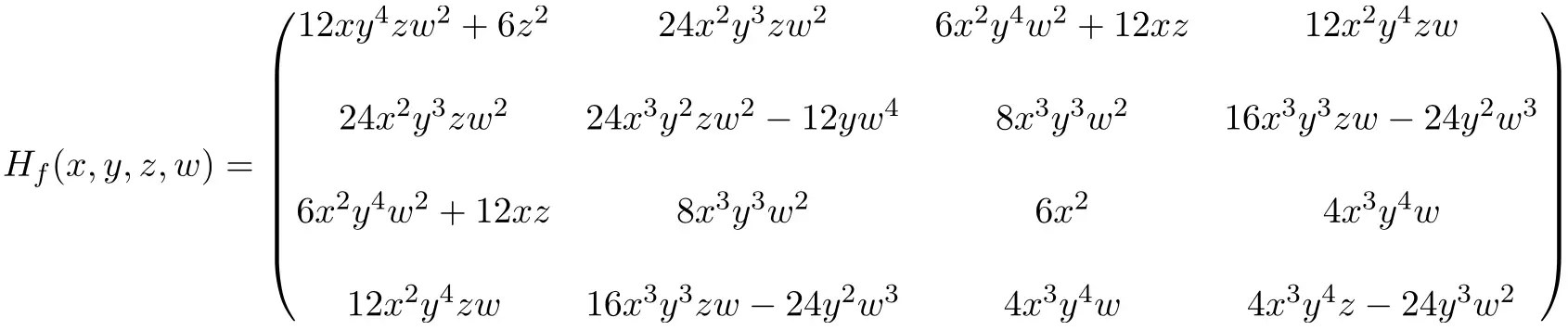
Son olarak bilinmeyenleri ilgili nokta değerlerinin (2,-1,1,-1) yerine koyarız ve hesaplamaları yaparız:
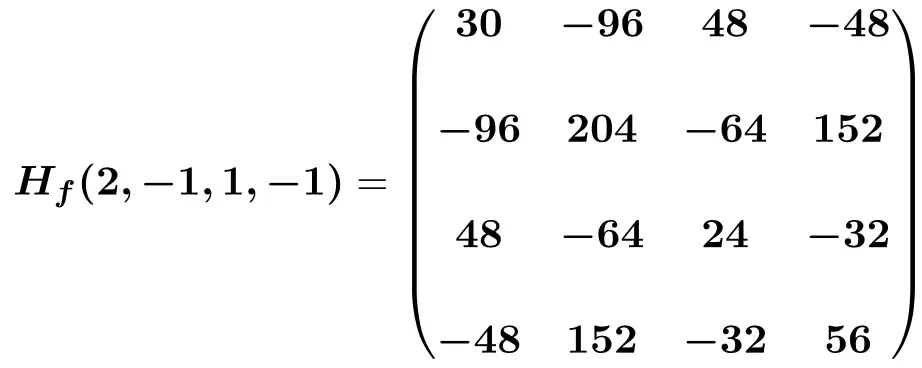
Hessian matrisinin pozitif, negatif veya belirsiz olduğunu nasıl anlarsınız?
Daha sonra göreceğimiz gibi, Hessian matrisinin pozitif yarı tanımlı, pozitif tanımlı, negatif yarı tanımlı, negatif tanımlı veya belirsiz matris olup olmadığını bilmek çok faydalıdır. Peki bunu nasıl öğrenebileceğimize bakalım:
Özdeğerlerin (veya özdeğerlerin) kriteri
Ne tür bir matris olduğunu bilmenin bir yolu, Hessian matrisinin özdeğerlerini (veya özdeğerlerini) incelemektir:
- Hessian matrisi, sıfıra eşit ve sıfırdan büyük özdeğerlere (veya özdeğerlere) sahipse pozitif yarı tanımlıdır . Yani pozitif özdeğerleri vardır ve en az biri 0’a eşittir:
![]()
- Hessian matrisi, tüm özdeğerleri (veya özdeğerleri) yalnızca 0’dan (pozitif) büyükse pozitif tanımlıdır :
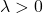 negatif yarı tanımlıdır . Yani negatif özdeğerleri vardır ve en az biri 0’a eşittir:
negatif yarı tanımlıdır . Yani negatif özdeğerleri vardır ve en az biri 0’a eşittir:
![]()
- Hessian matrisi, tüm özdeğerleri (veya özdeğerleri) 0’dan (negatif) küçükse negatif tanımlıdır :
![]()
- Hessian matrisi, pozitif ve negatif özdeğerlere (veya özdeğerlere) sahip olduğunda tanımsızdır :
![]()
Sylvester kriteri
Hessian matrisinin ne tür olduğunu bilmenin bir başka yolu Sylvester kriterini kullanmaktır, ancak bu teorem bize sadece pozitif tanımlı, negatif tanımlı veya belirsiz olup olmadığını bilmemizi sağlar. Ancak bazen hesaplamalar genellikle daha kolay olduğundan kullanımı çok daha hızlı olabilir.
Böylece Sylvester kriteri şu şekilde okunur:
- Hessian matrisinin tüm ana küçükleri 0’dan büyükse, bu pozitif tanımlı bir matristir.
- Hessian matrisinin çift indeksli asal küçükleri 0’dan büyük ve tek indeksli olanlar 0’dan küçükse negatif tanımlı bir matristir.
- Hessian matrisinin tüm ana küçükleri 0 değilse ve önceki iki koşulun hiçbiri karşılanmıyorsa, bu belirsiz bir matristir.
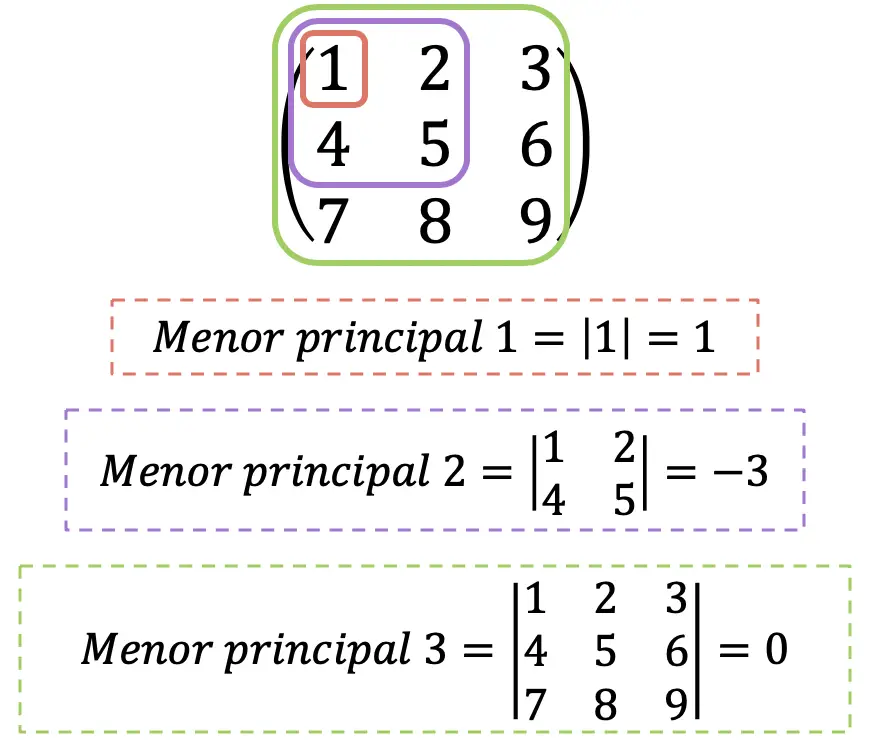
Açıkçası, Hessian matrisinin maksimum ana minörü her zaman determinantıyla çakışacaktır. Yalnızca bilgilendirme amaçlıdır, Hessian matrisinin determinantına “Hessian” da denir, ancak karışıklığı önlemek için burada bunu yapmayacağız.
Hessian matrisi ile bir fonksiyonun maksimum veya minimum değeri nasıl hesaplanır
Hessian matrisinin nasıl hesaplanacağını öğrendikten sonra muhtemelen merak ediyorsunuzdur: Peki bu matris ne için kullanılıyor?
Hessian matrisinin uygulamalarından biri de birden fazla değişkenli bir fonksiyonun maksimum veya minimumunu bulmaktır. Maksimum ve minimumların nasıl hesaplanacağına ilişkin adım adım açıklama aşağıda verilmiştir:
- Öncelikle çok değişkenli fonksiyonun kritik noktaları hesaplanır. Bunu yapmak için fonksiyonun gradyanını veya Jacobian matrisini hesaplıyoruz, 0’a eşitliyoruz ve denklemleri çözüyoruz.
- Hessian matrisi hesaplanır.
- Adım 1’de bulunan kritik noktalar Hessian matrisine yerleştirilir. Böylece kritik noktaların fonksiyona sahip olduğu sayıda Hessian matrisi elde edeceğiz.
- Her Hessian matrisinin ne tür bir matris olduğuna bakıyoruz. Yani pozitif tanımlı, negatif tanımlı, belirsiz vb. olup olmadığına bakıyoruz.
- Hessian matrisi pozitif tanımlı ise kritik nokta fonksiyonun göreceli minimumudur .
- Hessian matrisi negatif tanımlı ise kritik nokta fonksiyonun göreceli maksimumudur .
- Hessian matrisi tanımsızsa kritik nokta eyer noktasıdır .
Çok değişkenli bir fonksiyonun maksimum ve minimumlarını hesaplama örneği
Bunun nasıl yapıldığını görmek için burada Hessian matrisi kullanılarak bir fonksiyonun göreceli ekstremumlarının hesaplanmasına ve sınıflandırılmasına ilişkin bir örnek verilmiştir:
- Aşağıdaki çok değişkenli fonksiyonun tüm göreceli ekstremumlarını bulun:
![]()
Yapmamız gereken ilk şey, fonksiyonun Jacobian matrisini hesaplamaktır; bu durumda bu, skaler bir fonksiyon olduğu için gradyanla çakışacaktır:
![]()
Şimdi kritik noktaları belirlememiz gerekiyor, bunun için elde edilen denklemleri 0’a eşitliyoruz ve denklem sistemini çözüyoruz:
![]()
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d851eb626a9bd385aec8f68c9df71a39_l3.png)
Yani bulduğumuz kritik nokta (0,-2)’dir.
Fonksiyonun kritik noktası bulunduktan sonra Hessian matrisini hesaplamamız gerekir:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-702fa5f5c3e3d872e1ec0dad0e3216c7_l3.png)
Ve açıkçası, kritik noktada değerlendirilen Hessian matrisi aynıdır:
![Rendered by QuickLaTeX.com \displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b56ffff28d1a9b98c9848891ae924eb_l3.png)
Ne tür bir matris olduğunu görmek için Sylvester kriterini kullanacağız. Bu nedenle matrisin ana küçüklerini çözüyoruz:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8](https://mathority.org/wp-content/ql-cache/quicklatex.com-d66efe9fca481475009bb1703939e4f6_l3.png)
Asal minör 1 (tek) pozitiftir ve asal minör 2 (çift) negatiftir, dolayısıyla Sylvester kriterine göre belirsiz bir matristir. Ve bu nedenle kritik nokta (0,-2) bir eyer noktasıdır.
Hessian matrisi ile bir fonksiyonun içbükeyliğini veya dışbükeyliğini belirleme
Hessian matrisinin bir diğer kullanımı da bir fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmektir. Ve bu aşağıdaki teoreme göre belirlenebilir:
Olmak
![]()
açık bir küme ve
![]()
ikinci türevleri sürekli olan bir fonksiyonun içbükeyliği ve dışbükeyliği Hessian matrisi tarafından tanımlanır:
- İşlev

baştan sona dışbükeydir

ancak ve ancak Hessian matrisi kümenin her noktasında pozitif yarı tanımlı ise.
- İşlev

boyunca kesinlikle dışbükeydir

ancak ve ancak Hessian matrisinin kümenin her noktasında pozitif tanımlı olması durumunda.
✓ Bu nedenle eğer
![]()
Jacobian matrisinin de sıfırlandığı bir noktada dışbükey bir fonksiyondur, bu nokta yerel bir minimumdur .
- İşlev

genel olarak içbükeydir

ancak ve ancak Hessian matrisi kümenin her noktasında negatif yarı tanımlı ise.
- İşlev

genel olarak kesinlikle içbükeydir

ancak ve ancak Hessian matrisi kümenin her noktasında negatif tanımlıysa.
✓ Bu nedenle eğer
![]()
Jacobian matrisinin de sıfırlandığı bir noktada içbükey bir fonksiyondur, bu nokta yerel bir maksimumdur .
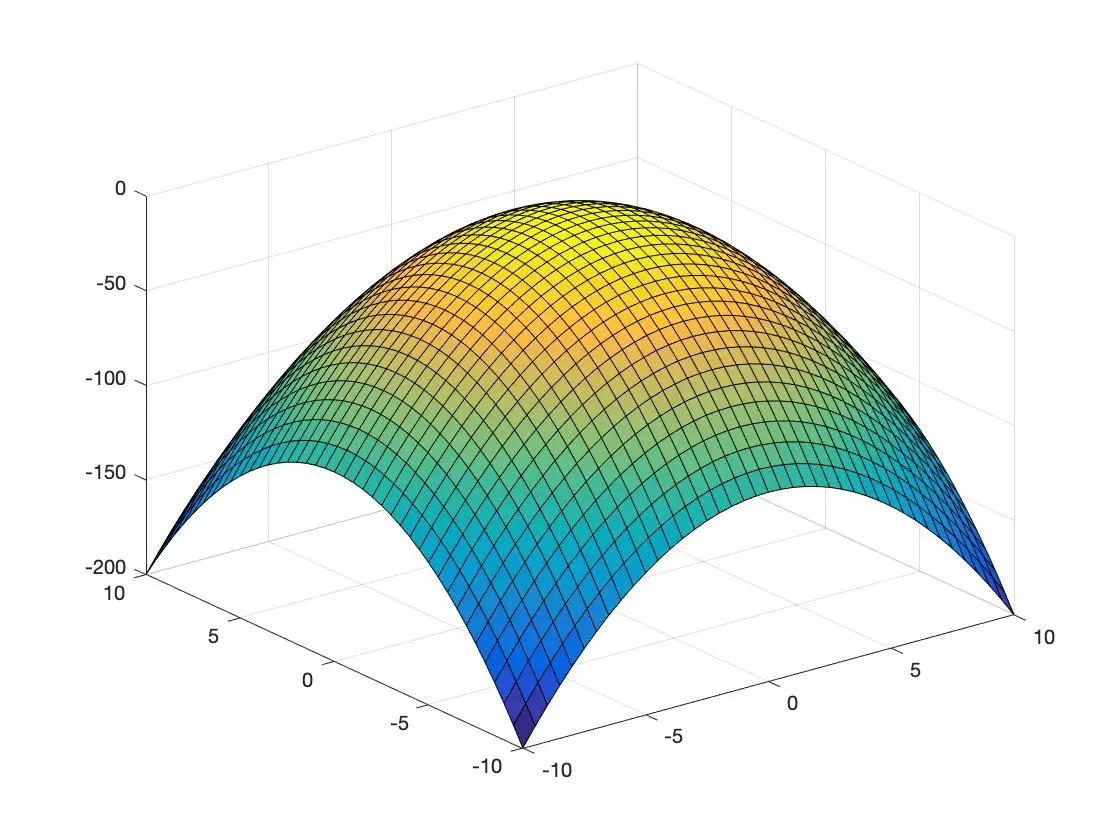
Aşağıda 3 boyutlu uzayda temsil edilen bir dışbükey fonksiyon ve bir başka içbükey fonksiyon örneğini görüyorsunuz:
dışbükey fonksiyon
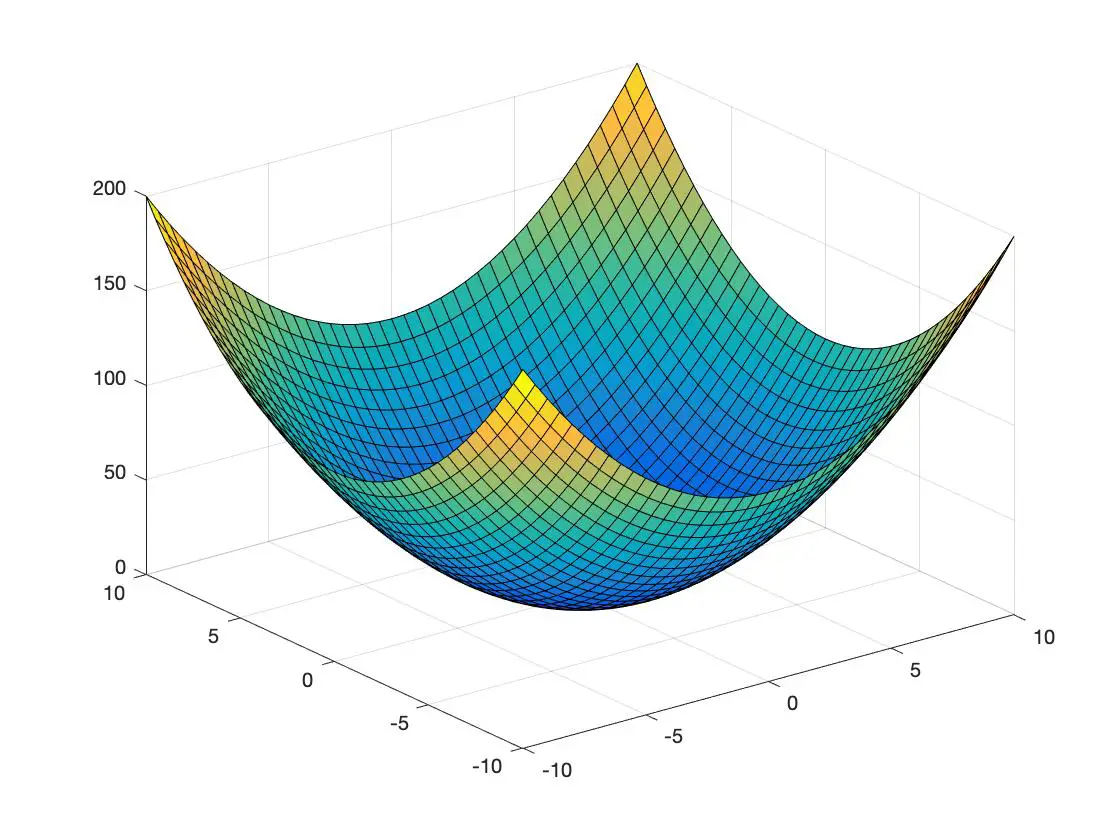
içbükey fonksiyon
Hessian matrisinin daha fazla uygulaması
Hessian matrisinin ana kullanım alanları daha önce gördüklerimizdir ancak başka uygulamaları da vardır. En çok merak edenler için aşağıda bunları açıklıyoruz.
Taylor polinomu
Taylor polinomunun 2 veya daha fazla değişkenli fonksiyonlar için açılımı
![]()
şöyle başlar:
![]()
Gördüğünüz gibi Taylor açılımının ikinci dereceden terimleri polinomun açılım noktasında değerlendirilen Hessian matrisi tarafından verilmektedir.
Kenarlıklı Çuval Bezi Matrisi
Hessian matrisinin bir başka kullanımı da çok değişkenli bir fonksiyonun minimum ve maksimumlarını hesaplamaktır.
![]()
başka bir rolle sınırlı
![]()
. Bu sorunu çözmek için sınırlı Hessian matrisi kullanılır ve aşağıdaki prosedür izlenir:
Adım 1: Aşağıdaki ifadeyle tanımlanan Lagrange fonksiyonu hesaplanır:
![]()
Adım 2: Lagrange fonksiyonunun kritik noktaları bulunur. Bunu yapmak için Lagrange fonksiyonunun gradyanını hesaplıyoruz, denklemleri 0’a eşitliyoruz ve denklemleri çözüyoruz.
![]()
![]()
Adım 3: Bulduğumuz her nokta için aşağıdaki matrisle tanımlanan sınırlı Hessian’ı hesaplıyoruz:
![Rendered by QuickLaTeX.com \displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3d1b2b04de9559a521e6704151c27bc4_l3.png)
Adım 4: Her kritik nokta için maksimum mu yoksa minimum mu olduğunu belirleriz:
- Bu, fonksiyonun yerel maksimumu olacaktır

fonksiyon kısıtlamaları altında
kritik noktada değerlendirilen sınırlanmış Hessian matrisinin son nm’si (burada n değişkenlerin sayısı ve m kısıtlamaların sayısıdır) negatif işaretle başlayan alternatif işaretlere sahipse.
- Bu, fonksiyonun yerel minimumu olacaktır

fonksiyon kısıtlamaları altında
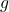
kritik noktada değerlendirilen keskin Hessian matrisinin son nm’sinin ( n değişkenlerin sayısı ve m’nin kısıtlamaların sayısı olduğu) ana küçüklerinin tümü negatif işaretlere sahipse.
Bir kısıtlı fonksiyonun diğerine göre göreceli minimum veya maksimumlarının, kısıtlanmamış fonksiyon için mutlaka böyle olması gerekmediği akılda tutulmalıdır. Sınırlı Hessian matrisi bu nedenle yalnızca bu tür problemler için kullanışlıdır.
Diğer operasyonlarla ilişki
Son olarak, Hessian matrisi aynı zamanda diğer önemli işlemlere veya matrislere, özellikle de Jacobian matrisine ve Laplace operatörüne bağlıdır.
Jacobian matrisiyle ilişki
Bir fonksiyonun Hessian matrisi
![]()
aynı fonksiyonun gradyanının Jacobian matrisidir :
![]()
Laplace operatörü
Hessian matris izi Laplace operatörüne eşdeğerdir:
![]()
Laplace operatörünün tanımı bir fonksiyonun gradyanının ıraksaması olduğundan bu eşitlik kolayca kanıtlanabilir:
![]()
Dolayısıyla ifadesi şu şekildedir:
![]()
Ve bu toplam Hessian matrisinin yalnızca izidir, dolayısıyla eşdeğerlik kanıtlanmıştır.