Hermit (veya Hermit) matrisi

Bu sayfada Hermit matrisi olarak da bilinen Hermit matrisinin ne olduğunu öğrenebilirsiniz. Hermit matrislerinin örneklerini, tüm özelliklerini ve bu tür matrislerin sahip olduğu formları, onları mükemmel bir şekilde anlayabilmek için bulacaksınız. Son olarak, herhangi bir karmaşık matrisin, Hermitsel matris artı bir anti-Hermitsel matrisin toplamına nasıl ayrıştırılacağını da açıklıyoruz.

Hermit veya Hermit matrisi nedir?

Hermit matrisi veya Hermit matrisi olarak da adlandırılan, eşlenik transpozesine eşit olma özelliğine sahip, karmaşık sayılara sahip bir kare matristir.

$A=A^*$

Altın

$A^*$

eşlenik devrik matrisidir

$A$

Meraktan dolayı, bu matris türü, matematikte, özellikle de doğrusal cebir alanında önemli araştırmalar yapan 19. yüzyıl Fransız matematikçisi Charles Hermite’nin onuruna adlandırılmıştır.

Bu matrisin bu şekilde isimlendirilmesinin nedeni, bu belirli matrislerin özdeğerlerinin (veya özdeğerlerinin) her zaman gerçek sayılar olduğunu göstermesiydi ancak bunu Hermitian Matrislerin Özellikleri bölümünde daha ayrıntılı olarak açıklayacağız.

Son olarak, bu matris bazen kendine eşlenik matris olarak da adlandırılabilir, ancak bu çok nadirdir.

Hermit matris örnekleri

Hermit matrisinin (veya Hermit matrisinin) tanımını gördükten sonra, farklı boyutlardaki Hermit matrislerinin bazı örneklerini görelim:

2 × 2 mertebesinden Hermit matrisi örneği

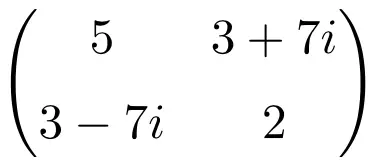
2x2 boyutunda Hermit veya Hermit matrisi

3 × 3 boyutlu Hermit matrisi örneği

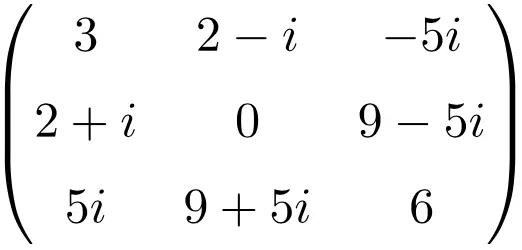
3x3 boyutunda Hermit veya Hermit matrisi

4 × 4 boyutunda Hermit matris örneği

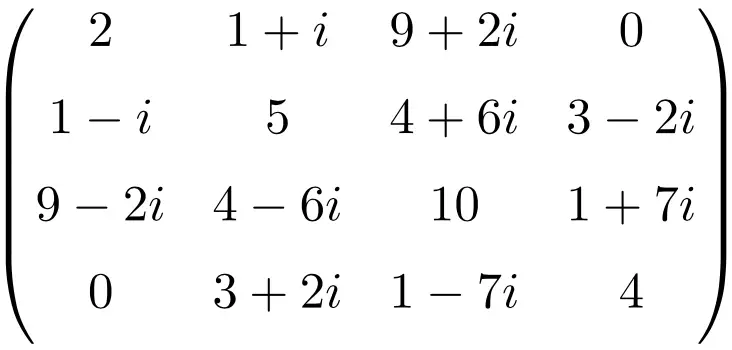
4x4 boyutunda Hermit veya Hermit matrisi

Bu matrislerin tümü Hermitseldir çünkü her birinin eşlenik transpoz matrisi matrisin kendisine eşittir.

Hermit matrisinin yapısı

Hermit matrisleri hatırlanması çok kolay bir yapıya sahiptir: ana köşegen üzerindeki gerçel sayılardan oluşurlar ve i’inci satırda ve j’inci sütunda yer alan karmaşık eleman, j’inci satırda bulunan elemanın eşleniği olmalıdır ve i’inci sütun.

İşte Hermit matris yapılarının bazı örnekleri.

2×2 Hermit yapısı

$\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}$

3×3 Hermit yapısı

$\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}$

4×4 Hermit yapısı

$\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}$

Hermit matrisinin özellikleri

Şimdi bu tip kare karmaşık matrisin özelliklerinin neler olduğunu göreceğiz:

Herhangi bir Hermit matrisi normal bir matristir . Her ne kadar normal matrislerin tümü Hermit matrisleri olmasa da.

Herhangi bir Hermit matrisi köşegenleştirilebilir. Ayrıca elde edilen diyagonal matris yalnızca gerçek elemanları içerir.

Bu nedenle, bir Hermit matrisinin özdeğerleri (veya özdeğerleri) her zaman gerçek sayılardır. Bu özellik Charles Hermite tarafından keşfedilmiştir ve bu nedenle bu çok özel matrise Hermitian adını vermekten onur duymuştur.

Benzer şekilde, bir Hermit matrisinin özuzayları ikiye iki diktir:
$\mathbb{C}^n$

matrisin özvektörlerinden (özvektörlerinden) oluşur.

Gerçek sayılardan oluşan bir matris, yani hiçbir elemanın imajiner kısmı olmadığı anlamına gelir, ancak ve ancak simetrik bir matris olması durumunda Hermitian’dır. Örneğin 2×2 birim matris gibi.

Bir Hermit matrisi, gerçek bir simetrik matris ile hayali bir antisimetrik matrisin toplamı olarak ifade edilebilir.

$A =B+Ci$

İki Hermit matrisinin toplamı (veya çıkarılması) başka bir Hermit matrisine eşittir çünkü:

$(A\pm B)^* = A^*\pm B^* = A \pm B$

Bir Hermit matrisinin bir skalerle çarpımının sonucu, eğer skaler bir gerçek sayı ise başka bir Hermit matrisidir.

$(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A$

İki Hermit matrisinin çarpımı genellikle artık Hermit matrisi değildir. Bununla birlikte, iki matris değiştirilebilir olduğunda, yani iki matrisin çarpımının sonucu, çarpılma yönüne bakılmaksızın aynı olduğunda, çarpım Hermitseldir, çünkü o zaman eşlenik devrik işlemlerinin aşağıdaki koşulu matrisler:

$(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B$

Bir Hermit matrisi tersinirse, bunun tersi de bir Hermit matrisi olur.

$(A^{-1})^* = (A^*)^{-1} = A^{-1}$

Bir Hermit matrisinin determinantı her zaman gerçek bir sayıya eşdeğerdir. İşte bu özelliğin kanıtı:

$det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}$

Susuz

$A = A^*$

$det(A) = \overline{det(A)}$

Bu nedenle, bu koşulun karşılanması için Hermit matrisinin determinantının mutlaka gerçek bir sayı olması gerekir. Bu şekilde sonucun eşleniği sonucun kendisine eşit olur.

Karmaşık bir matrisin Hermit matrisine ve Hermit karşıtı matrise ayrıştırılması

Karmaşık elemanlara sahip herhangi bir matris , bir Hermit matrisi artı başka bir Hermit karşıtı matrisin toplamına ayrıştırılabilir . Ancak bunun için bu tür matrislerin aşağıdaki özelliklerini bilmeniz gerekir:

Bir kare kompleks matris artı bunun transpoze eşleniğinin toplamı bir Hermit matrisini verir.

$C + C^* = \text{Matriz Hermitiana}$

Bir kare kompleks matris ile onun transpoze eşleniği arasındaki fark, bir anti-Hermit (veya anti-Hermit) matrisi verir.

$C - C^* = \text{Matriz Antihermitiana}$

Bu nedenle, tüm karmaşık matrisler bir Hermit matrisi ve bir anti-Hermit matrisinin toplamına ayrıştırılabilir. Bu teorem Teoplitz ayrışımı olarak bilinir:

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

C, ayrıştırmak istediğimiz karmaşık matris olduğunda, C* onun transpoze eşleniğidir ve son olarak A ve B, C matrisinin ayrıştırıldığı sırasıyla Hermit ve anti-Hermit matrisleridir.

Hermit (veya hermit) matrisi