Üniter matris - Mathority

Bu sayfada üniter matrisin ne olduğunu açıklıyoruz ve ayrıca iyi anlaşılması için çeşitli alıştırmalarla örnekliyoruz. Ayrıca bu tip matrislerin lineer cebir için çok önemli olan özelliklerinin neler olduğunu da keşfedeceksiniz.

Üniter matris nedir?

Üniter matrisin tanımı aşağıdaki gibidir:

Üniter bir matris, eşlenik devrik matrisi ile çarpıldığında birim matrise eşit olan karmaşık bir matristir. Yani aşağıdaki koşul karşılanmıştır:

$U\cdot U^* = U^* \cdot U =I$

Altın

$U$

üniter bir matristir ve

$U^*$

onun konjuge transpozu.

Bu nedenle, bu koşul , bir birim matrisin tersinin onun eşlenik devriği olduğunu ima eder, çünkü ters bir matrisin tanımına göre, bir matris, eğer ürünü d’identify matrisine eşdeğerse, diğerinin tersidir. .

$\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}$

Bu nedenle, üniter bir matris her zaman düzenli veya dejenere olmayan bir matris olacaktır, çünkü her zaman tersi olacaktır.

Öte yandan, bir üniter matrisin gerçek sayı ortamındaki analoğu dik matristir ve bu durumda üniter matrisin devri ile çarpılmasının birim matrise eşit olduğu doğrudur.

$U\cdot U^t = U^t \cdot U =I$

Yani bu durumda U’nun ters matrisi doğrudan onun transpoze (veya transpoze) matrisi olacaktır.

Birim matris örnekleri

2×2 boyutlu birim matris örneği

Birim matris kavramını gördükten sonra, bunu daha iyi anlamak için 2×2 birim matris örneğini göreceğiz:

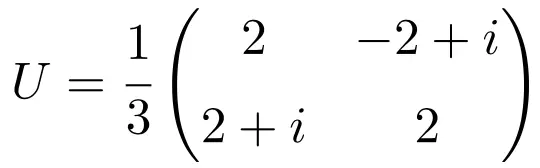
Bu matris üniterdir çünkü kendisinin eşlenik matrisiyle çarpımı Kimlik (veya Birim) matrisini verir:

$\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Ve daha önce gördüğümüz gibi, herhangi bir üniter matris eşlenik devri ile değiştirilebilir:

$\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Birim Köşegen Matris Örneği

Yalnızca i karmaşık sayısından oluşan köşegen matris , matrisin boyutundan bağımsız olarak üniter bir matris örneğidir. Aşağıda bunu 3 × 3 boyutunda bir birim matrisle gösteren çözülmüş bir alıştırma var:

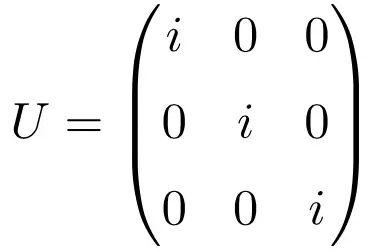
Matrisin çarpımını eşlenik devriyle çözersek, bunun çözüm olarak Kimlik matrisini verdiğini unutmayın:

$\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

Matrisleri tersten çarptığımızda da aynı şey olur:

$\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

Bu matrisin özelliği, herhangi bir boyuttaki üniter bir matrisin bir örneği olarak hizmet etmesidir, çünkü matris her seferinde ana köşegen üzerindeki hayali sayı i tarafından oluşturulur ve elemanların geri kalanı sıfırdır (0) ) üniter bir matris olacaktır.

Üniter bir matrisin özellikleri

Birim matrislerin özellikleri aşağıdaki gibidir:

Açıkçası, herhangi bir üniter matris normal bir matristir . Her ne kadar normal matrislerin tümü üniter matrisler olmasa da.

Üniter matrisler her zaman kare matrislerdir .

Tüm birim matrisler köşegenleştirilebilir, yani köşegen matrislere dönüştürülebilir.

Birim matrisin determinantının mutlak değeri her zaman 1’e eşittir.

$\begin{vmatrix} det(U) \end{vmatrix} = 1$

Özdeş matris üniter bir matristir.

hepsi için
$n$

, tüm birim matrislerin kümesi

$n\times n$

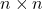
matris çarpım işlemi ile birim grup adı verilen bir grup oluştururlar.

Böylece aynı mertebeden iki birim matrisin çarpımı başka bir birim matris verir.

Bir birim matrisin tüm özdeğerlerinin (veya özdeğerlerinin) modülü her zaman 1’e eşittir.

$\begin{vmatrix} \lambda \end{vmatrix} = 1$

Bu tip matrislerin özuzayları diktir.

Üniter matris nedir?

Birim matris örnekleri

2×2 boyutlu birim matris örneği

Birim Köşegen Matris Örneği

Üniter bir matrisin özellikleri

Yorum bırakın Yanıtı iptal et