Bu sayfada karmaşık matrislerin, eşlenik matrislerin ve eşlenik devrik matrislerin ne olduğunu göreceksiniz. Şimdi size çok benziyorlar, ancak sayfanın sonunda her biri arasındaki farkı nasıl tam olarak anlayacağınızı göreceksiniz. Ayrıca her türün örneklerini ve özelliklerini göreceğiz.
karmaşık matris
Eşlenik matris ve devrik eşlenik matrisin açıklamasını görmeden önce, karmaşık matris kavramına bir göz atalım:
Karmaşık matris nedir?
Karmaşık bir matris, elemanları arasında belirli bir karmaşık sayıya sahip olan bir matristir.
Karmaşık veya sanal bir sayının, i harfiyle gösterilen, bir gerçek kısım ve sanal bir kısımdan oluşan bir sayı olduğunu hatırlayın. Örneğin:
![]()
.
Karmaşık matris örnekleri
Karmaşık çok boyutlu dizilerin bazı örneklerine bakalım:
2 × 2 mertebesinden karmaşık matris örneği
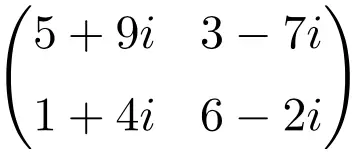
3×3 boyutunda karmaşık bir matris örneği
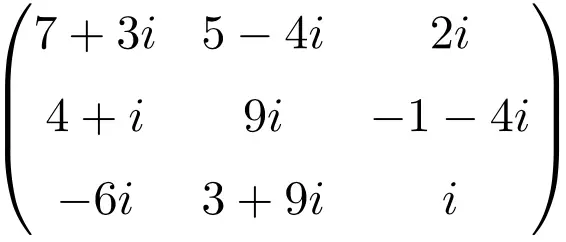
4×4 boyutunda karmaşık bir matris örneği
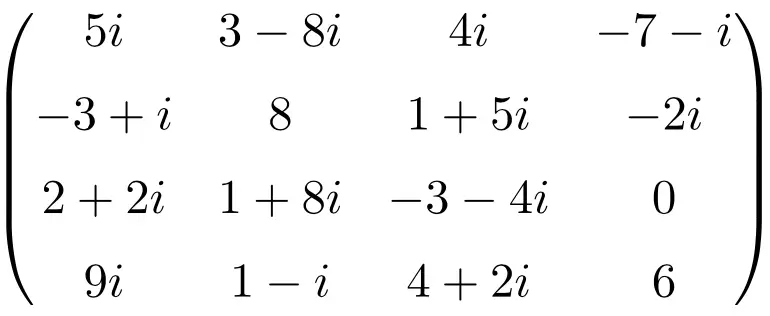
eşlenik matris
Karmaşık bir matrisin tanımının ne olduğunu gördükten sonra, bir eşlenik matrisin ve bir devrik eşlenik matrisin ne olduğuna bakalım:
Eşlenik matris nedir?
Eşlenik matris, tüm elemanlarının eşlenikleriyle değiştirildiği, yani tüm karmaşık sayılarının sanal kısmının işaretinin değiştirildiği karmaşık bir matristir.
eşlenik matrisi
![]()
yukarıda yatay bir çubukla ifade edilir:
![]()
.
Eşlenik matris örneği
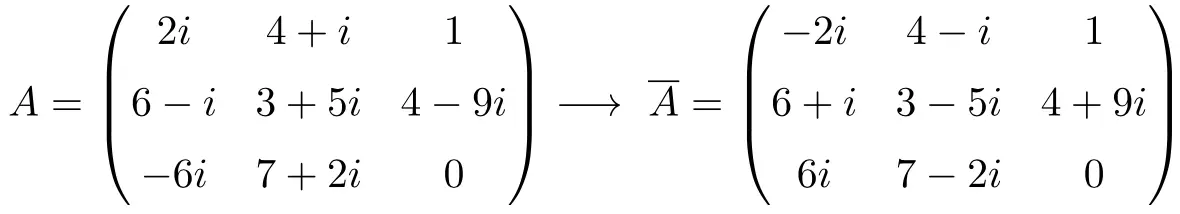
Eşlenik matrisin özellikleri
Bu tip matrisin özellikleri aşağıdaki gibidir:
- Bir eşlenik matrisin eşleniği orijinal matristir.
![]()
- İki matrisin toplanması (veya çıkarılması) ve sonucun eşleştirilmesi, önce iki matrisin ayrı ayrı eşlenmesi ve ardından bunların eklenmesi (veya çıkarılması) ile aynıdır.
![]()
- İki matrisin eşlenik çarpımı , iki matrisin ayrı ayrı eşleniklenmesine ve ardından matris çarpımının hesaplanmasına eşittir.
![]()
- Bir matrisi bir skalerle çarpmak ve sonucu eşleniklemek, önce skaler ile matrisin eşleniklerini yapıp ardından çarpımı çözmekle aynıdır.
![]()
- Bir matrisin transpoze edilmesi ve ardından konjuge edilmesi, önce matrisin konjuge edilmesi ve sonra transpoze edilmesi anlamına gelir.
![]()
- Bir matrisin tersini alıp onu eşlemek, matrisi eşleyip sonra ters çevirmekle aynıdır.
![]()
- Bir eşlenik matrisin sırası, aynı eşlenik olmayan matrisin sırasına eşittir.
![]()
- Konjuge bir matrisin izini hesaplamak veya aynı matrisin izini konjuge olmadan hesaplamak ve ardından sonucu eşleniklemek fark etmez.
![]()
- Son olarak, bir eşlenik matrisin determinantını almak, aynı matrisin eşlenik olmadan determinantının sonucunun eşlenik değerini hesaplamak için yeterlidir.
![]()
Eşlenik devrik matrisi
Son olarak, bir matrisin nasıl eşlenikleneceğini gördükten sonra, eşlenik devrik matris kavramına geçelim:
Eşlenik devrik (veya devrik) matrisi nedir?
Transpoze edilmiş (veya transpoze edilmiş) konjuge matris, bir matrisin transpoze edilmesi ve ardından konjugatının yapılmasından sonra elde edilen matristir.
Bu tür matrislere aynı zamanda ek matris veya basitçe ek matris de denir. Ek olarak, genellikle bir yıldız işaretiyle temsil edilir
![]()
olarak çizen matematikçiler olmasına rağmen
![]()
herhangi biri
![]()
.
Eşlenik Transpoze Matrisi Örneği
Aşağıda bir matrisin devriğini (veya eşlenik devriğini) hesaplamanın bir örneği verilmiştir:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
İlk önce A matrisini transpoze ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
Daha sonra devriğin eşlenik matrisini hesaplıyoruz, başka bir deyişle tüm karmaşık sayıların sanal kısmının işaretini değiştiriyoruz:
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
Bu nedenle, eşlenik devrik matrisinin hesaplanmasının özeti şu şekildedir:
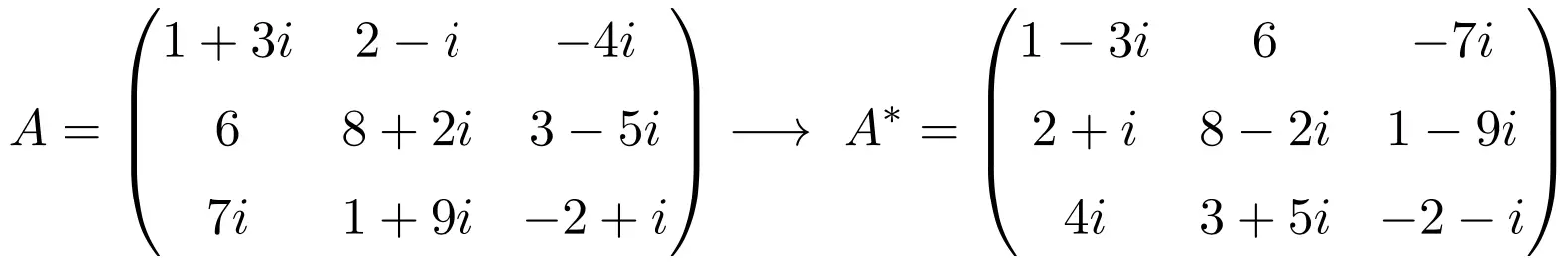
Eşlenik devrik matrisinin özellikleri
Bu tip kare matrisin özellikleri aşağıdaki gibidir:
- Daha önce transpoze edilmiş ve konjuge edilmiş bir matrisin konjuge transpoze matrisi , orijinal matristir.
![]()
- Eşlenik devrik matrislerin toplama özelliği , iki matrisin eklenmesinin (veya çıkarılmasının) ve ardından bu işlemin sonuca uygulanmasının, önce her matrisin eşlenik devrini yapıp ardından sonuçların eklenmesine (veya çıkarılmasına) eşdeğer olduğunu belirtir.
![]()
- İki matrisin çarpılması ve ardından eşlenik devrinin yapılması, eşlenik devrik matrislerin ters çarpımı ile aynı sonucu verir.
![]()
- Bir skaler ve bir matrisin çarpımının eşlenik transpoz matrisini hesaplamak, karmaşık sayıyı eşlenikleyip matrisin eşlenik transpozunu ayrı ayrı bulup sonra çarpmakla aynıdır.
![]()
- Matris ters çevrilebilirse, matris ters çevirme ve eşlenik devrik işlemlerinin gerçekleştirilme sırası önemsizdir.
![]()