Bu sayfada bir polinomun bağımsız teriminin ne olduğunu ve nasıl hesaplandığını açıklıyoruz. Ek olarak, farklı polinomların bağımsız terimlerini nasıl tanımlayacağınıza dair birkaç örnek görebileceksiniz ve hatta çözülmüş alıştırmalarla pratik yapabileceksiniz.
Bir polinomun bağımsız terimi nedir?
Bir polinomun bağımsız teriminin tanımı aşağıdaki gibidir:
Matematikte bir polinomun bağımsız terimi, değişkeni olmayan terimdir. Bu nedenle bir polinomun bağımsız terimi, polinomun sıfır dereceli monomiyaline karşılık gelir.
Örneğin aşağıdaki polinomun bağımsız terimi 7’dir:
![]()
Bir önceki örnekteki polinomda harf kısmı olmayan yani x’i olmayan terim 7 sayısıdır. Bu nedenle söz konusu polinomun bağımsız terimi 7’dir.
Bir polinomun bağımsız terimi çok basit bir kavram gibi görünse de bazı polinom hesaplamaları için oldukça faydalı olduğunu bilin. Örneğin, bir polinomun köklerini bulma prosedürü onun bağımsız teriminde başlar. Bir polinomun köklerini (veya sıfırlarını) nasıl bulacağınız hakkında daha fazla bilgi edinmek istiyorsanız bu bağlantıya göz atabilir, burada örnekleri de görebilir ve adım adım çözülen alıştırmalarla pratik yapabilirsiniz.
Bağımsız polinom terimleri örnekleri
Bir polinomun bağımsız teriminin anlamını öğrendikten sonra, bir polinomun bağımsız teriminin nasıl bulunacağına dair birkaç örnek göreceğiz:
- 4. derece bir polinomun bağımsız terimine örnek:
![]()
Bu örnekteki polinom tek bir polinomdur ve değişkeni olmayan terim 5’tir, dolayısıyla polinomun bağımsız teriminin değeri 5’tir.
- 5. derece bir polinomun bağımsız terimine örnek:
![]()
Bu polinomun x değişkeninin eşlik etmediği elemanı -2’dir, dolayısıyla polinomun bağımsız terimidir. Sayının negatif işaretinin de bağımsız terime dahil olduğuna dikkat edin.
- 8. derece bir polinomun bağımsız terimine örnek:
![]()
Bu polinomdaki tüm tek terimlilerin +1 dışında bir değişkeni vardır, dolayısıyla polinomun bağımsız terimi +1’dir.
Son olarak, bağımsız terimin özelliklerinden biri, x=0 için bir polinomun sayısal değerinin her zaman bağımsız terimine eşit olmasıdır. Bu merakla daha fazla ilgileniyorsanız, bağlantılı sayfada bir polinomun sayısal değerinin nasıl hesaplandığına danışabilirsiniz, ayrıca bunun nasıl yapıldığına dair birkaç örnek bulacaksınız ve çözülmüş alıştırmalarla pratik yapabileceksiniz. adım adım.
Bir polinomun bağımsız terimiyle ilgili çözülmüş alıştırma
Bir polinomun bağımsız teriminin ne olduğunu özümsemeyi tamamlamak için aşağıda çözeceğimiz alıştırmayı yapmanızı öneririz:
- Polinom göz önüne alındığında
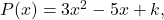
bağımsız terimin değerini hesaplar

böylece doldurulur
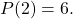
Bu sorunu çözmek için yapılacak ilk şey, belirlemeye çalışmaktır.
![]()
Henüz:
![]()
Gücü hesaplıyoruz:
![]()
Çarpma işlemlerini yapıyoruz:
![]()
Ve terim olarak çıkarıyoruz:
![]()
Dolayısıyla ifadenin şartının sağlanması için elde edilen cebirsel ifadenin 6’ya eşitlenmesi gerekir:
![]()
![]()
Bu nedenle ortaya çıkan denklemi çözmek yeterlidir:
![]()
![]()
Sonuç olarak polinomun bağımsız terimi 4 olmalıdır.
Son olarak, Ruffini kuralını doğru bir şekilde uygulamak için bir polinomun bağımsız teriminin de önemli olduğunu bilmelisiniz. Ne olduğunu bilmiyorsanız Ruffini kuralı polinomları hızla bölmek için kullanılan bir yöntemdir. Burada Ruffini kuralının nasıl uygulanacağını ve bunun bir polinomun bağımsız terimiyle nasıl ilişkili olduğunu görebilirsiniz.