Skaler matris - Mathority

Bu sayfada skaler matrisin ne olduğunu ve mükemmel bir şekilde anlaşılabilmesi için skaler matrislerin birkaç örneğini bulacaksınız. Ayrıca skaler matrislerin tüm özelliklerini ve onlarla işlem yapmanın avantajlarını görebileceksiniz. Son olarak bir skaler matrisin determinantının nasıl hesaplanacağını ve bu tür bir matrisin nasıl ters çevrileceğini açıklıyoruz.

Skaler matris nedir?

Skaler matris, ana köşegendeki tüm değerlerin eşit olduğu köşegen bir matristir .

Bu bir skaler matrisin tanımıdır, ancak örneklerle daha iyi anlaşılacağına eminim: 😉

Skaler Dizi Örnekleri

2×2 mertebesinde bir skaler matris örneği

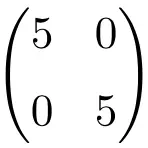
3×3 skaler matris örneği

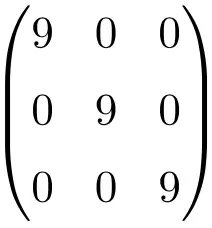
4×4 boyutunda bir skaler matris örneği

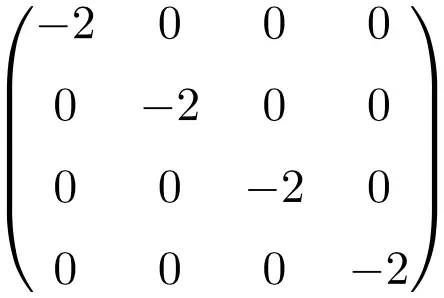
Skaler matrislerin özellikleri

Skaler matris aynı zamanda köşegen bir matristir, dolayısıyla bu matris sınıfının birçok özelliğini miras aldığını göreceksiniz:

Tüm skaler matrisler aynı zamanda simetrik matrislerdir .

Bir skaler matris hem bir üst üçgen matris hem de bir alt üçgen matristir .

Kimlik matrisi skaler bir matristir.

Herhangi bir skaler matris, bir birim matris ile bir skaler sayının çarpımından elde edilebilir.

$4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}$

Sıfır matrisi aynı zamanda bir skaler matristir.

Bir skaler matrisin özdeğerleri (veya özdeğerleri), ana köşegeninin elemanlarıdır. Dolayısıyla özdeğerleri her zaman aynı olacak ve matrisin boyutu kadar tekrarlanacaktır.

$\begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8$

Bir skaler matrisin eki başka bir skaler matristir. Ve dahası, eklenen matrisin ana köşegeninin değerleri her zaman matrisin mertebesine yükseltilen orijinal matrisin değerleri olacaktır – 1 .

$\displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}$

Skaler matrislerle işlemler

Skaler matrislerin lineer cebirde bu kadar yaygın kullanılmasının nedenlerinden biri de hesaplama yapmanıza olanak sağlamasıdır. Bu nedenle matematikte çok önemlidirler.

Şimdi bu tür kare matrislerle hesaplama yapmanın neden bu kadar kolay olduğunu görelim:

Skaler matrislerin toplanması ve çıkarılması

İki skaler matrisin toplanması (ve çıkarılması) çok basittir: sadece ana köşegenlerdeki sayıları ekleyin (veya çıkarın). Örneğin:

$\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}$

Skaler matris çarpımı

Toplama ve çıkarmaya benzer şekilde, iki skaler matris arasındaki çarpma veya matris çarpımını çözmek için aralarındaki köşegenlerin elemanlarını çarpmanız yeterlidir. Örneğin:

$\displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}$

Skaler matrislerin gücü

Bir skaler matrisin gücünü hesaplamak da çok basittir: köşegenin her bir elemanını üsse yükseltmeniz gerekir. Örneğin:

 *** QuickLaTeX cannot compile formula:
\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^ 4 & 0 & 0 \\[1.1ex] 0 & 2^

*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \right. inserted.
leading text: \end{document}

& 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 ve 16 \end{pmatrix}

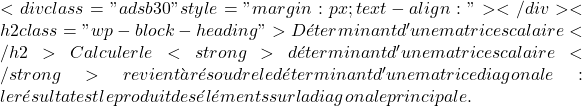
$<div class="adsb30" style=" margin:px; text-align:"></div> <h2 class="wp-block-heading"> Déterminant d’une matrice scalaire</h2> <p> Calculer le <strong>déterminant d’une matrice scalaire</strong> revient à résoudre le déterminant d’une matrice diagonale : le résultat est le produit des éléments sur la diagonale principale.” title=”Rendered by QuickLaTeX.com” height=”106″ width=”582″ style=”vertical-align: -4px;”></p> <p> \displaystyle \text{det}(A)= \prod_{i =1}^n a_i</p> <p class=$ $Regardez l'exercice résolu suivant dans lequel on trouve le déterminant d'une matrice scalaire en multipliant les éléments de sa diagonale principale :$

\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm {343}

$En fait, puisque tous les éléments de la diagonale principale d'une matrice scalaire sont toujours égaux, pour trouver le résultat du déterminant, il suffit d'augmenter le numéro de la diagonale principale du nombre de fois qu'elle est répétée. Par conséquent, l'exercice précédent peut également être résolu de la manière suivante :$

\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343}

$Démontrer ce théorème est très simple : il suffit de calculer le déterminant d'une matrice scalaire par blocs (ou cofacteurs). Vous trouverez ci-dessous la <strong>démonstration</strong> de la formule utilisant une matrice scalaire générique :” title=”Rendered by QuickLaTeX.com” height=”62″ width=”1060″ style=”vertical-align: -4px;”></p> <p> \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{ vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} – 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \ begin{vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) – 0 \cdot 0 + 0 \cdot 0 \\[ 2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{aligned}</p> <p class=$ $Dans ce cas ça donne$

a^3

$car la matrice est d'ordre 3, mais il faut toujours l'élever à l'ordre de la matrice. <div class="adsb30" style=" margin:12px; text-align:center"> <div id="ezoic-pub-ad-placeholder-118"></div> </div> <h2 class="wp-block-heading"> Inverser une matrice scalaire</h2> <p> Une matrice scalaire <strong>est inversible si, et seulement si, tous les éléments de la diagonale principale sont différents de 0</strong> . Dans ce cas on dit que la matrice scalaire est une matrice régulière. De plus, l’inverse d’une matrice scalaire sera toujours une autre matrice scalaire avec les <strong>inverses</strong> de la diagonale principale :” title=”Rendered by QuickLaTeX.com” height=”174″ width=”1250″ style=”vertical-align: -5px;”></p> <p> \displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1 }=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{ 1}{9} \end{pmatrix}</p> <p class=$ $D'autre part, de la caractéristique précédente, on peut déduire que le déterminant d'une matrice scalaire inversée est le résultat de la multiplication des inverses de la diagonale principale :$

\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = 0,125 ABD doları