Burada bir kuvvetin (veya potansiyel fonksiyonun) nasıl elde edileceğini açıklıyoruz, bir kuvvetin türevinin formülünü, birkaç örneği bulacaksınız ve hatta adım adım çözülen alıştırmalarla pratik yapabilirsiniz.
Bir gücün türevinin formülü
Bir kuvvetin veya potansiyel fonksiyonun türevi, kuvvet üssü çarpı üssün üsse yükseltilmiş hali eksi 1 çarpı bazın türevinin çarpımıdır.
![]()
Bu nedenle, eğer taban özdeşlik fonksiyonu ise, kuvveti elde etmek için, fonksiyonu üsle çarpmanız ve üssünden bir birim çıkarmanız yeterlidir:
![]()
Gerçekten de kimlik fonksiyonunun türevi 1’e eşittir.
Özetle, potansiyel bir fonksiyonu türetmek için iki formül vardır: birincisi her zaman kullanılabilir, ikincisi ise yalnızca taban x olduğunda uygulanabilir.
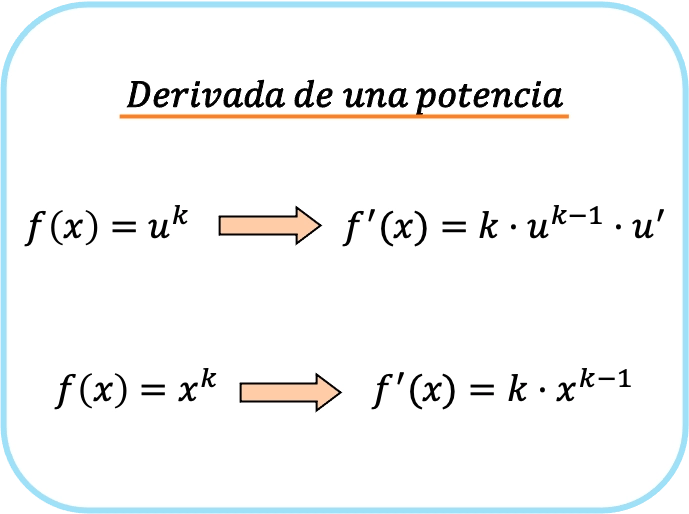
Bir kuvvetin türevi için sunulan ilk formülün ikinciye benzediğini ancak zincir kuralını uyguladığını kolaylıkla doğrulayabiliriz.
Bu formüllerin yalnızca değişkenin üssü olması durumunda kullanılabileceğini unutmayın; x paydadaysa üstel bir fonksiyonun türevine ilişkin kuralı uygulamanız gerekir:
➤ Bakınız: üstel bir fonksiyonun türevi
Güç Türevlerine Örnekler
Bir potansiyel fonksiyonun türevinin formülünü gördükten sonra, kuvvetlerin nasıl türetildiğini anlamanız için bu türevin birkaç örneğini açıklayacağız.
Örnek 1: Temel kuvvet x’in türevi
![]()
Önceki bölümde açıkladığımız gibi kuvvetin tabanı yalnızca x olduğunda fonksiyonu türetmek için kullanmamız gereken formül şu şekildedir:
![]()
Dolayısıyla x kuvvetinin 4 kuvvetine yükseltilmiş türevi:
![]()
Örnek 2: Parantezli kuvvetin türevi
![]()
Bu örnekte taban özdeşlik fonksiyonu değildir, dolayısıyla bir kuvvetin türevi için genel formülü kullanmalıyız:
![]()
Parantez içindeki fonksiyon doğrusal bir fonksiyon olduğundan türevi 2’dir. Dolayısıyla tüm potansiyel fonksiyonun türevi şöyledir:
![]()
Örnek 3: Negatif kuvvetin türevi
![]()
Bu durumda, üssü negatif ve tabanı logaritma olan bir potansiyel fonksiyonumuz var, dolayısıyla fonksiyonun türevini almak için aşağıdaki formülü kullanacağız:
![]()
Kuvvet üssü negatif olsa bile ondan bir de çıkarılmalıdır. Dolayısıyla fonksiyonun türevi şu şekildedir:
![]()
Çözümle ilgili herhangi bir şüpheniz varsa, logaritmik bir fonksiyonun türevinin formülüne buradan bakabilirsiniz:
➤ Bakınız: logaritmik bir fonksiyonun türevi
Örnek 4: Köklü bir kuvvetin türevi
![]()
Bu örnekteki işlev, düzenli ifade içindeki bir kuvvettir. Bununla birlikte, radikaller potansiyel ifadelere dönüştürülebilir, böylece fonksiyon, kesirli üslü bir potansiyel fonksiyona dönüştürülerek basitleştirilebilir:
![]()
Şimdi bir değişkenin kuvvetinin türevi için formülü uyguluyoruz:
![]()
Ve türevi:
![]()
Ayrıca kök türev kuralını kullanarak bu tür fonksiyonların ayrımını da yapabilirsiniz:
➤ Bakınız: bir kökten türetilmiştir
Bir gücün türevine ilişkin çözülmüş alıştırmalar
Aşağıdaki kuvvetlerin türevini hesaplayın:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
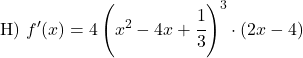
![]()