Parametreli denklem sistemlerinin tartışılması -

Bu sayfada parametrelerle bir denklem sistemini nasıl tartışacağımızı ve çözeceğimizi göreceğiz. Ek olarak, doğrusal denklem sistemlerinin örneklerini ve çözülmüş alıştırmalarını bulacaksınız.

Öte yandan, doğrusal denklem sistemlerini analiz etmek için Cramer kuralının ve Rouché-Frobenius teoreminin ne olduğunu bilmeniz önemlidir çünkü bunları sürekli kullanacağız.

Parametreli doğrusal denklem sistemi örneği

Aşağıdaki denklem sistemini m parametresi cinsinden tartışın ve çözün:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

Şimdi matrisin kaçıncı sırada olduğunu görmek için A’nın determinantını Sarrus kuralını kullanarak çözeceğiz:

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

Yani A’nın determinantının sonucu m’nin değerine bağlıdır. Bu nedenle determinantın hangi m değerleri için ortadan kaybolduğunu göreceğiz. Bunu yapmak için sonucu 0’a eşitledik :

$\displaystyle m^2-5m+6 = 0$

Ve ikinci dereceden denklemi aşağıdaki formülle çözüyoruz:

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

Yani m 2 veya 3’e eşit olduğunda A’nın determinantı 0 olacaktır. Ve m 2’den farklı ve 3’ten farklı olduğunda A’nın determinantı 0’dan farklı olacaktır.

Bu nedenle her durumu ayrı ayrı analiz etmeliyiz:

m≠3 ve m≠2:

Az önce gördüğümüz gibi m parametresi 2 ve 3’ten farklı olduğunda A matrisinin determinantı 0’dan farklıdır. Dolayısıyla A’nın rütbesi 3’tür .

$\displaystyle rg(A)=3$

Üstelik A’ matrisinin rütbesi de 3’tür , çünkü içinde determinantı 0’dan farklı olan 3×3’lük bir alt matris vardır. Ve ‘4×4’lük bir determinant yapamadığımız için’ rütbesi 4 olamaz.

$\displaystyle rg(A')=3$

O halde, A matrisinin rütbesi, A’ matrisinin rütbesine ve sistemin bilinmeyen sayısına (3) eşit olduğundan, Rouché-Frobenius teoremi ile bunun Kararlı Sistem Uyumlu (SCD) olduğunu biliyoruz. :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Sistemin Uyumlu Belirlenmiş Sistem (DCS) olduğunu bildiğimizde, onu çözmek için Cramer kuralını uygularız. Bunu yapmak için A matrisinin, determinantının ve A’ matrisinin şöyle olduğunu hatırlayın:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

X’i Cramer kuralıyla hesaplamak için, A matrisinin determinantının ilk sütununu bağımsız terimler sütunuyla değiştiririz ve onu A’nın determinantına böleriz:

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

Y’yi Cramer kuralıyla hesaplamak için A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına böleriz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

Z’yi Cramer kuralıyla hesaplamak için A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına böleriz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

Dolayısıyla m≠3 ve m≠2 durumu için denklem sisteminin çözümü şöyledir:

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

Gördüğünüz gibi bu durumda denklem sisteminin çözümü m’nin bir fonksiyonudur.

m’nin 2 ve 3’ten farklı olduğu durumun çözümünü bulduğumuzda, m’nin 2’ye eşit olduğu durum için sistemi çözeceğiz:

m=2:

Şimdi m parametresi 2’ye eşit olduğunda sistemi analiz edeceğiz. Bu durumda A ve A’ matrisleri şöyledir:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

Daha önce gördüğümüz gibi m=2 olduğunda A’nın determinantı 0’dır. Bu nedenle A matrisinin derecesi 3 değildir. Ancak içinde 0’dan farklı 2×2 determinantı vardır, örneğin:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Yani bu durumda A’nın rütbesi 2’dir :

$\displaystyle rg(A)=2$

A matrisinin rütbesini bildiğimizde, A’ matrisinin rütbesini hesaplarız. İlk 3 sütunun determinantı 0 verir, dolayısıyla A’ matrisindeki diğer olası 3×3 determinantları deneriz:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

3×3 boyutunun tüm olası determinantları 0 verir. Ancak, A’ matrisinin A matrisiyle aynı 2×2 0 olmayan determinantına sahip olduğu açıktır:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

Bu nedenle A’ matrisi de rütbe 2’dedir :

$\displaystyle rg(A')=2$

Yani, A matrisinin rütbesi A’ matrisinin rütbesine eşit olduğundan, ancak bu ikisi (3) sisteminin bilinmeyen sayısından küçük olduğundan, Rouché-Frobenius teoreminden şunu biliyoruz: Bu Belirsiz Olarak Uyumlu Bir Sistemdir (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Bu bir ICS olduğundan, bunu çözmek için sistemi dönüştürmemiz gerekiyor. Bunu yapmak için öncelikle sistemden bir denklemi çıkarmalıyız, bu durumda son denklemi sileceğiz:

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

Şimdi z değişkenini λ’ya dönüştürelim:

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

Ve λ’lı terimleri bağımsız terimlerle birlikte koyarız:

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

Bu nedenle, sistemin A matrisi ve A’ matrisi kalır:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

Son olarak sistemi dönüştürdükten sonra Cramer kuralını uyguluyoruz . Bunu yapmak için önce A’nın determinantını çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

X’i Cramer kuralıyla hesaplamak için A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip onu A’nın determinantına böleriz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

Y’yi Cramer kuralıyla hesaplamak için A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına böleriz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

Böylece m=2 olduğunda denklem sisteminin çözümü λ’nın bir fonksiyonudur, çünkü bu bir SCI’dir ve dolayısıyla sonsuz çözümlere sahiptir:

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

m parametresi 2 ve 3’ten farklı olduğunda ve 2’ye eşit olduğunda sistemin çözümünü zaten analiz etmiştik. Bu nedenle yalnızca son duruma ihtiyacımız var: m 3 değerini aldığında:

m=3:

Şimdi m parametresi 3 olduğunda ne olacağını analiz edeceğiz. Bu durumda A ve A’ matrisleri şöyledir:

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

Daha önce de gördüğümüz gibi, m=3 olduğunda A’nın determinantı 0’dır. Yani A matrisinin derecesi 3 değildir. Ancak içinde 0’dan farklı 2×2 determinantı vardır, örneğin:

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

Yani bu durumda A’nın rütbesi 2’dir :

$\displaystyle rg(A)=2$

A matrisinin rütbesini bildiğimizde, A’ matrisinin rütbesini hesaplarız. İlk 3 sütunun determinantı 0 verir, bu nedenle A’ matrisinin içindeki başka bir 3×3 determinantı deneriz, örneğin son 3 sütununki:

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

Öte yandan, A’ matrisi, sonucu 0’dan farklı olan bir determinant içerir, dolayısıyla A’ matrisi 3. sıradadır :

$\displaystyle rg(A')=3$

Dolayısıyla m = 3 olduğunda A matrisinin rütbesi A’ matrisinin rütbesinden daha düşüktür. Böylece Rouché-Frobenius teoreminden sistemin Uyumsuz Sistem (IS) olduğu sonucunu çıkarıyoruz :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Bu nedenle m = 3 olduğunda denklem sisteminin çözümü yoktur.

Örneğin özeti:

Görüldüğü gibi denklem sisteminin çözümü m parametresinin değerine bağlıdır. İşte olası tüm durumların özeti:

m≠3 ve m≠2:

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

m=2:

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

m=3:

$\displaystyle \bm{SI} \longrightarrow$

Sistemin çözümü yok.

Burada tüm süreci Rouche teoremini ve Cramer kuralını kullanarak yaptık, ancak parametreli denklem sistemleri de Gauss yöntemiyle (alıştırmalarla) tartışılıp çözülebilir. Bu yöntem hakkında daha fazla bilgiyi, prosedürün ayrıntılı bir açıklamasının yanı sıra örnekler ve adım adım çözülmüş alıştırmalar bulacağınız bağlantılı sayfada bulabilirsiniz.

Parametreli Doğrusal Denklem Sistemlerinin Çözülmüş Tartışma Problemleri

1. Egzersiz

Aşağıdaki parametreye bağlı doğrusal denklem sistemini tartışın ve çözün:

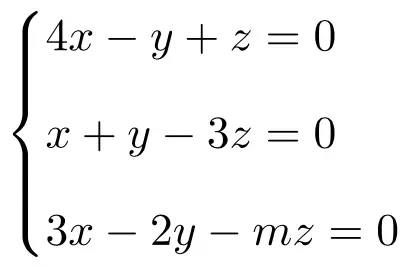
Parametreli denklem sistemlerinin çözülmüş alıştırması

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

Şimdi A matrisinin rütbesini bulmalıyız. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ederiz:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

A’nın determinantının sonucu m’nin değerine bağlıdır. Bu nedenle determinantın hangi m değerleri için ortadan kaybolduğunu göreceğiz. Bunu yapmak için ortaya çıkan sonucu 0’a eşitliyoruz ve denklemi çözüyoruz:

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

Yani m -4 olduğunda A’nın determinantı 0 olacaktır. m -4’ten farklı olduğunda A’nın determinantı 0’dan farklı olacaktır. Bu nedenle her durumu ayrı ayrı analiz etmeliyiz:

m≠-4:

Az önce gördüğümüz gibi m parametresi -4’ten farklı olduğunda A matrisinin determinantı 0’dan farklıdır. Dolayısıyla A’nın rütbesi 3’tür.

$\displaystyle rg(A)=3$

Üstelik A’ matrisinin rütbesi de 3’tür, çünkü içinde determinantı 0’dan farklı olan 3×3’lük bir alt matris vardır. Ve ‘4×4’lük bir determinant yapamadığımız için’ rütbesi 4 olamaz.

$\displaystyle rg(A')=3$

Bu nedenle, Rouché-Frobenius teoremini uygulayarak bunun uyumlu bir belirli sistem (SCD) olduğunu biliyoruz çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

Sistemin bir SCD olduğunu bildiğimizde, onu çözmek için Cramer kuralını uygularız. Bunu yapmak için A matrisinin, determinantının ve A’ matrisinin şöyle olduğunu hatırlayın:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

Xatex’i Cramer kuralıyla hesaplamak için, A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştiririz ve bunu A’nın determinantına böleriz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Bilinmeyeni hesaplamak için Cramer kuralına göre A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirir ve onu A’nın determinantına böleriz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Z’yi Cramer kuralıyla hesaplamak için A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına böleriz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

Dolayısıyla m≠-4 durumu için denklem sisteminin çözümü şöyledir:

x=0 y=0 z=0

m=-4:

Şimdi m parametresi -4 olduğunda sistemi analiz edeceğiz. Bu durumda A ve A’ matrisleri şöyledir:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

Daha önce gördüğümüz gibi, m=-4 olduğunda A’nın determinantı 0’dır. Yani A matrisinin derecesi 3 değildir. Ancak içinde 0’dan farklı 2×2 determinantı vardır, örneğin:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Matrisin 2. dereceden 0’dan farklı bir determinantı olduğundan, A matrisi 2. derecedendir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, dolayısıyla diğer olası 3×3 determinantları deneyeceğiz:

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

A’ matrisinin tüm 3×3 determinantları 0’dır, dolayısıyla A’ matrisi de 3. sırada olmayacaktır. Ancak içinde 0’dan farklı 2. dereceden determinantlar bulunur. Örneğin:

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

Yani A’ matrisi rütbe 2’de olacaktır:

$\displaystyle rg(A')=2$

A matrisinin boyutu A’ matrisinin boyutuna eşittir ancak bu ikisi sistemdeki (3) bilinmeyenlerin sayısından daha küçüktür, dolayısıyla Rouché-Frobenius teoremine göre c bir Belirsiz Uyumlu Sistemdir (ICS):

Bu bir ICS sistemi, dolayısıyla bunu çözmek için sistemi dönüştürmemiz gerekiyor. Öncelikle bu durumda sonuncusu olacak olan bir denklemi ortadan kaldırıyoruz:

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

Şimdi z değişkenini λ’ya dönüştürelim:

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

Ve λ’lı terimleri bağımsız terimlerle birlikte koyarız:

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

Öyle ki sistemin A matrisi ve A’ matrisi şöyle kalır:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

Son olarak sistemi dönüştürdükten sonra Cramer kuralını uyguluyoruz. Bunu yapmak için önce A’nın determinantını çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

X’i Cramer kuralıyla hesaplamak için A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip onu A’nın determinantına böleriz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

Bilinmeyeni hesaplamak için Cramer kuralına göre A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirir ve onu A’nın determinantına böleriz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

Böylece m=-4 olduğunda denklem sisteminin çözümü λ’nın bir fonksiyonudur, çünkü bu bir SCI’dir ve dolayısıyla sonsuz çözümlere sahiptir:

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

Alıştırma 2

Aşağıdaki parametreye bağlı doğrusal denklem sistemini tartışın ve çözümünü bulun:

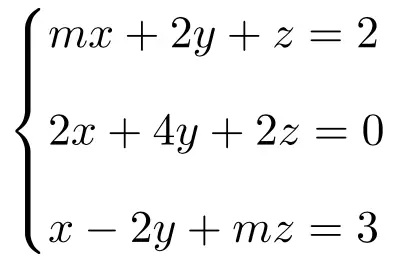
egzersiz parametrelerle doğrusal denklemlerin adım adım çözülmesini sağlar

çözümü gör

Yapılacak ilk şey sistemin A matrisi ve genişletilmiş A’ matrisidir:

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

Şimdi A matrisinin rütbesini bulmalıyız. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ederiz:

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

Yani m +1 veya -1 olduğunda A’nın determinantı 0 olacaktır. m +1 ve -1’den farklı olduğunda A’nın determinantı 0’dan farklı olacaktır. Bu nedenle her durumu şu şekilde analiz etmeliyiz:

m≠+1 ve m≠-1:

Az önce gördüğümüz gibi m parametresi +1 ve -1’den farklı olduğunda A matrisinin determinantı 0’dan farklıdır. Dolayısıyla A’nın rütbesi 3’tür.

$\displaystyle rg(A)=3$

$\displaystyle rg(A')=3$

Sistemin bir SCD olduğunu bildiğimizde, onu çözmek için Cramer kuralını uygularız. Bunu yapmak için A matrisinin, determinantının ve A’ matrisinin şöyle olduğunu hatırlayın:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

X’i Cramer kuralıyla hesaplamak için A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip onu A’nın determinantına böleriz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

Bilinmeyeni hesaplamak için Cramer kuralına göre A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirir ve onu A’nın determinantına böleriz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

Z’yi Cramer kuralıyla hesaplamak için A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına böleriz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

Dolayısıyla m≠+1 ve m≠-1 durumu için denklem sisteminin çözümü şöyledir:

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

m=+1:

Şimdi m parametresi 1’e eşit olduğunda sistemi analiz edeceğiz. Bu durumda A ve A’ matrisleri şöyledir:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

Daha önce gördüğümüz gibi, m=+1 olduğunda A’nın determinantı 0’dır. Yani A matrisinin derecesi 3 değildir. Ancak içinde 0’dan farklı 2×2 determinantı vardır, örneğin:

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

Matrisin 2. dereceden 0’dan farklı bir determinantı olduğundan, A matrisi 2. derecedendir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, bu yüzden şimdi örneğin son 3 sütunun determinantını deneyeceğiz:

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

Öte yandan, A’ matrisi, sonucu 0’dan farklı olan 3×3’lük bir determinant içerir, dolayısıyla A’ matrisi 3. sıradadır:

$\displaystyle rg(A')=3$

Dolayısıyla m=+1 olduğunda A matrisinin rütbesi A’ matrisinin rütbesinden küçüktür. Böylece Rouché-Frobenius teoreminden sistemin Uyumsuz Sistem (IS) olduğu sonucunu çıkarıyoruz:

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Bu nedenle denklem sisteminin m=+1 olduğunda çözümü yoktur çünkü uyumsuz bir sistemdir.

m=-1:

Şimdi m parametresi -1 olduğunda sistemi analiz edeceğiz. Bu durumda A ve A’ matrisleri şöyledir:

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

Daha önce gördüğümüz gibi, m=-1 olduğunda A’nın determinantı 0’dır. Yani A matrisinin derecesi 3 değildir. Ancak içinde 0’dan farklı 2×2 determinantı vardır, örneğin:

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

Matrisin 2. dereceden 0’dan farklı bir determinantı olduğundan, A matrisi 2. derecedendir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, bu yüzden şimdi örneğin 1, 3 ve 4 numaralı sütunların determinantını deneyeceğiz:

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

Öte yandan, A’ matrisi, sonucu 0’dan farklı olan 3×3’lük bir determinant içerir, dolayısıyla A’ matrisi 3. sıradadır:

$\displaystyle rg(A')=3$

Dolayısıyla m = -1 olduğunda A matrisinin rütbesi A’ matrisinin rütbesinden daha düşüktür. Böylece Rouché-Frobenius teoreminden sistemin Uyumsuz Sistem (IS) olduğu sonucunu çıkarıyoruz:

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Bu nedenle denklem sisteminin m=-1 olduğunda uyumsuz bir sistem olması nedeniyle çözümü yoktur .

Parametreli doğrusal denklem sistemi örneği

Örneğin özeti:

Parametreli Doğrusal Denklem Sistemlerinin Çözülmüş Tartışma Problemleri

1. Egzersiz

Alıştırma 2

Yorum bırakın Yanıtı iptal et