Rouche-Frébenius teoremi

Bu sayfada Rouché Frobenius teoreminin ne olduğunu ve bununla bir matrisin rütbesinin nasıl hesaplanacağını keşfedeceğiz. Ayrıca Rouché-Frobenius teoremi ile adım adım çözülmüş örnekler ve alıştırmalar bulacaksınız.

Rouché-Frobenius teoremi nedir?

Rouché-Frobenius teoremi, doğrusal denklem sistemlerini sınıflandırmak için kullanılan bir yöntemdir. Başka bir deyişle Rouché-Frobenius teoremi, bir denklem sisteminin çözülmesine gerek kalmadan kaç çözümü olduğunu bulmak için kullanılır.

3 tür denklem sistemi vardır:

Sistem Uyumluluğu Belirlendi (SCD): Sistemin kendine özgü bir çözümü vardır.
Belirsiz uyumlu sistem (ICS): Sistemin sonsuz çözümü vardır.
Sistem Uyumsuz (SI): Sistemin çözümü yoktur.

Ayrıca Rouché-Frobenius teoremi daha sonra Cramer kuralını kullanarak sistemleri çözmemize de olanak tanıyacaktır.

Rouché-Frobenius teoreminin ifadesi

Rouché-Frobenius teoremi şunu söylüyor:

$\displaystyle \bm{A}$

bir denklem sisteminin bilinmeyenlerinin katsayılarından oluşan matristir. ve göbek

$\displaystyle \bm{A'}$

veya genişletilmiş matris , bir denklem sisteminin bilinmeyenlerinin katsayıları ve bağımsız terimlerden oluşan matristir:

Rouché-Frobenius teoremi, A ve A’ matrislerinin sırasına göre ne tür bir denklem sistemiyle uğraştığımızı bilmemizi sağlar:

Eğer rütbe(A) = rütbe(A’) = bilinmeyenlerin sayısı ise ⟶ Belirlenen uyumlu sistem (SCD)
Eğer rütbe(A) = rütbe(A’) < bilinmeyenlerin sayısı ⟶ Belirsiz uyumlu sistem (SCI)
eğer aralık(A)
$\bm{\neq}$

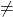
aralık (A’) ⟶ Uyumsuz sistem (SI)

Rouché-Frobenius teoreminin ne söylediğini öğrendikten sonra Rouché-Frobenius teoremi alıştırmalarını nasıl çözeceğimizi göreceğiz. İşte 3 örnek: her tür denklem sisteminin teoremi kullanılarak çözülmüş bir alıştırma.

Belirlenen uyumlu sistem örneği (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

Sistemin A matrisi ve genişletilmiş A’ matrisi şunlardır:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

Şimdi A matrisinin rütbesini hesaplıyoruz. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ediyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Matrisin 0’dan farklı bir 3×3 determinantı olduğundan, A matrisinin derecesi 3’tür:

$\displaystyle rg(A)=3$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız, bu en az 3. sıra olacaktır çünkü az önce 0’dan farklı 3. dereceden bir determinantı olduğunu gördük. üstelik, 4. sıra olamaz, çünkü 4. dereceden herhangi bir determinant yapamayız. Bu nedenle, A’ matrisi de 3. derecedendir:

$\displaystyle rg(A')=3$

Böylece A matrisinin rütbesi, A’ matrisinin rütbesine ve sistemin bilinmeyen sayısına (3) eşit olduğundan, Rouché Frobenius teoreminden bunun Uyumlu Belirlenmiş Sistem (SCD) olduğunu biliyoruz. :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Belirsiz uyumlu sistem (ICS) örneği

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

Sistemin A matrisi ve genişletilmiş A’ matrisi şunlardır:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

Şimdi A matrisinin rütbesini hesaplıyoruz. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ediyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

A matrisinin tamamının determinantı 0 verir, yani rütbesi 3 değildir. Derecesi 2 olup olmadığını görmek için A’da determinantı 0’dan farklı olan bir alt matris bulmalıyız. Örneğin, sol üst köşeden :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Matrisin 0’dan farklı bir 2×2 determinantı olduğundan, A matrisinin derecesi 2’dir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, dolayısıyla diğer olası 3×3 determinantları deneyeceğiz:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

A’ matrisinin tüm 3×3 determinantları 0’dır, dolayısıyla A’ matrisi de 3. sırada olmayacaktır. Ancak içinde 0’dan farklı 2. dereceden determinantlar bulunur. Örneğin:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Yani A’ matrisi 2. sırada olacaktır :

$\displaystyle rg(A')=2$

A matrisinin boyutu A’ matrisinin boyutuna eşittir ancak bunlar sistemin bilinmeyen sayısından azdır (3). Bu nedenle Rouché-Frobenius teoremine göre belirsiz uyumlu bir sistemdir (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Uyumsuz sistem örneği (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

Sistemin A matrisi ve genişletilmiş A’ matrisi şunlardır:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

Şimdi A matrisinin rütbesini hesaplıyoruz. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ediyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Matrisin 2. dereceden 0’dan farklı bir determinantı olduğundan, A matrisi 2. derecedendir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, bu yüzden şimdi örneğin son 3 sütunun determinantını deneyeceğiz:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

Öte yandan, A’ matrisi sonucu 0’dan farklı olan bir determinant içerir, bu nedenle A’ matrisinin derecesi 3 olacaktır :

$\displaystyle rg(A')=3$

Bu nedenle, A matrisinin rütbesi A’ matrisinin rütbesinden küçük olduğundan, Rouché-Frobenius teoreminden bunun bir Uyumsuz Sistem (SI) olduğu sonucunu çıkarırız :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Rouché-Frobenius teoreminin çözülmüş sorunları

1. Egzersiz

Rouché-Frobenius teoremini kullanarak aşağıdaki 3 bilinmeyenli denklem sisteminin türünü belirleyin:

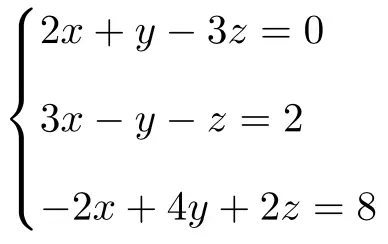
Rouche teoreminin çözülmüş alıştırması - frobenius

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

Şimdi A matrisinin rütbesini bulmalıyız. Bunu yapmak için matrisin determinantının 0’dan farklı olup olmadığını kontrol ediyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

Üçüncü dereceden determinantı 0’dan farklı olan matris A matrisinin derecesi 3’tür:

$\displaystyle rg(A)=3$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. Bu en azından rütbe 3 olacaktır, çünkü az önce içinde 0’dan farklı 3 mertebesinde bir determinant bulunduğunu gördük. Ayrıca 4×4 determinant yapamayacağımız için rütbe 4 olamaz. Bu nedenle A’ matrisi de 3. sıradadır:

$\displaystyle rg(A')=3$

Böylece, Rouché-Frobenius teoremi sayesinde bunun belirli uyumlu bir sistem (SCD) olduğunu biliyoruz çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

Alıştırma 2

Rouché-Frobenius teoremini kullanarak aşağıdaki 3 bilinmeyenli denklem sistemini sınıflandırın:

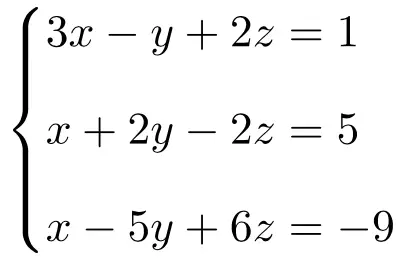
Rouche-Frobenius teoreminin çözülmüş alıştırması

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini oluşturuyoruz:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Şimdi A matrisinin aralığını hesaplayalım:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

Yani A matrisinin derecesi 2’dir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, dolayısıyla diğer olası 3×3 determinantları deneyeceğiz:

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

A’ matrisinin tüm 3×3 determinantları 0’dır, dolayısıyla A’ matrisi de 3. sırada olmayacaktır. Ancak içinde 0’dan farklı, 2. dereceden birçok determinant vardır. Örneğin:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Yani A’ matrisi 2. sırada olacaktır :

$\displaystyle rg(A')=2$

A matrisinin rütbesi A’ matrisinin rütbesine eşittir ancak bu ikisi sistemin bilinmeyen sayısından azdır (3). Bu nedenle Rouché-Frobenius teoreminden bunun belirsiz uyumlu bir sistem (ICS) olduğunu biliyoruz:

Alıştırma 3

Rouché-Frobenius teoremini kullanarak aşağıdaki denklem sisteminin ne tür bir sistem olduğunu belirleyin:

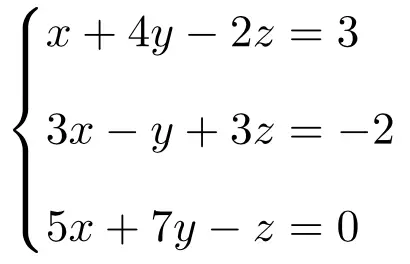
Rouche teoreminin adım adım çözüldüğü egzersiz - frobenius

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Şimdi A matrisinin aralığını hesaplayalım:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

Yani A matrisinin derecesi 2’dir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini ancak son 3 sütunun determinantının vermediğini zaten biliyoruz:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Bu nedenle, A’ matrisinin derecesi 3’tür :

$\displaystyle rg(A')=3$

A matrisinin rütbesi A’ matrisinin rütbesinden küçüktür, bu nedenle Rouché-Frobenius teoreminden bunun bir Uyumsuz Sistem (SI) olduğu sonucunu çıkarabiliriz :

Alıştırma 4

Rouché-Frobenius teoremini kullanarak aşağıdaki 3 bilinmeyenli denklem sisteminin türünü belirleyin:

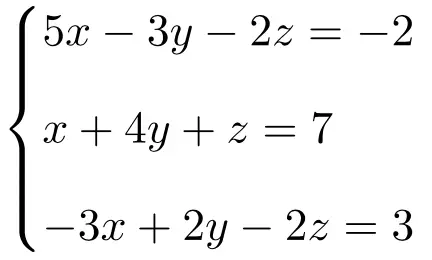
Rouche - Frobenius teoremi 3 bilinmeyen ve 3 denklemle çözüldü

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

Şimdi A matrisinin rütbesini hesaplamamız gerekiyor. Bunu yapmak için matrisin determinantını Sarrus kuralıyla çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

Üçüncü dereceden determinantı 0’dan farklı olan matris A matrisinin derecesi 3’tür:

$\displaystyle rg(A)=3$

Bu nedenle, A’ matrisi de rütbe 3’tür , çünkü her zaman en azından derece A’dır ve herhangi bir 4×4 determinantını çözemediğimiz için derece 4 olamaz.

$\displaystyle rg(A')=3$

Böylece, Rouché-Frobenius teoreminin uygulanması sayesinde sistemin bir Uyumlu Belirlenmiş Sistem (SCD) olduğunu biliyoruz çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

Alıştırma 5

Rouché-Frobenius teoremini kullanarak aşağıdaki denklem sisteminin ne tür bir sistem olduğunu belirleyin:

Çözüme bakın

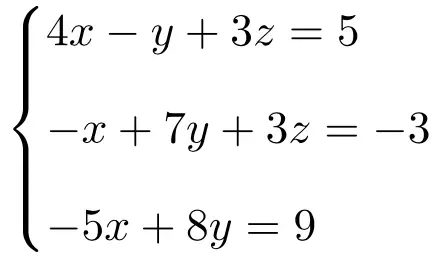
İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Şimdi A matrisinin aralığını hesaplayalım:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

Matris A bu nedenle 2. sıradadır:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. Zaten bildiğimiz ilk 3 sütunun determinantı 0 veriyor ancak son 3 sütunun determinantı şunu vermiyor:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Bu nedenle, A’ matrisinin derecesi 3’tür :

$\displaystyle rg(A')=3$

Ve son olarak, alanı Rouché-Frobenius teoremine uyguluyoruz: A matrisinin alanı, A’ matrisinin alanından daha küçüktür, dolayısıyla bir Uyumsuz Sistemdir (SI) :

Alıştırma 6

Aşağıdaki 3. dereceden denklem sistemini Rouché-Frobenius teoremine göre sınıflandırın:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini oluşturuyoruz:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Şimdi A matrisinin aralığını hesaplayalım:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Yani A matrisinin derecesi 2’dir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. İlk 3 sütunun determinantının 0 verdiğini zaten biliyoruz, dolayısıyla diğer olası 3×3 determinantları deneyeceğiz:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

A’ matrisinin tüm 3×3 determinantları 0’dır, dolayısıyla A’ matrisi de rütbe 3 olmayacaktır. Ancak içinde 0’dan farklı 2. dereceden determinantlar bulunur. Örneğin:

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Yani A’ matrisi 2. sırada olacaktır :

$\displaystyle rg(A')=2$

Son olarak, Rouché-Frobenius teoremini uygulayarak bunun bir Belirsiz Uyumlu Sistem (ICS) olduğunu biliyoruz, çünkü A matrisinin aralığı A’ matrisinin aralığına eşittir ancak bu ikisi matristeki bilinmeyenlerin sayısından daha küçüktür. sistem(3):

Rouche-frébenius teoremi

Rouché-Frobenius teoremi nedir?

Rouché-Frobenius teoreminin ifadesi

Belirlenen uyumlu sistem örneği (SCD)

Belirsiz uyumlu sistem (ICS) örneği

Uyumsuz sistem örneği (IS)

Rouché-Frobenius teoreminin çözülmüş sorunları

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Yorum bırakın Yanıtı iptal et