Bu bölümde bir denklem sistemini Gauss-Jordan yöntemiyle nasıl tartışacağımızı ve çözeceğimizi göreceğiz. Yani, bunun belirli uyumlu bir sistem (DCS), belirsiz uyumlu bir sistem (ICS) veya uyumsuz bir sistem olup olmadığını belirleyin. Ayrıca kavramları mükemmel bir şekilde uygulayabilmeniz ve özümseyebilmeniz için örnekler ve çözümlü alıştırmalar bulacaksınız.
Bundan sonra ne anlatacağımızı anlamak için Gauss yöntemini kullanarak bir sistemi nasıl çözeceğinizi zaten bilmeniz önemlidir, bu yüzden devam etmeden önce bir göz atmanızı öneririz.
Gauss yöntemiyle belirlenen uyumlu sistemler
Gauss matrisinin son satırı olduğu sürece
![]()
, olmak
![]()
Ve
![]()
herhangi iki sayı, bu bir SCD’dir (Sistem Uyumluluğu Belirlendi). Bu nedenle sistemin kendine özgü bir çözümü vardır .
Sistemlerin büyük çoğunluğu SCD’dir.
Örnek:
Örneğin şu sistemimiz var:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bab5d5823e45833aa691a3510a2a23eb_l3.png)
Kimin genişletilmiş matrisi:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 3x+8y+z=1\\[2ex] 6x+4y-z=-1 \end{array} \right\}} \ \longrightarrow \ \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f8daea11edeedfd6b86bb251fe19032_l3.png)
Sistemi çözmek için matrisin satırları üzerinde işlem yapmamız ve ana köşegenin altındaki tüm elemanları 0’a dönüştürmemiz gerekir. Yani ikinci satırdan ilk satırı çıkarırız ve üçüncü satırdan da ilk satırı 2 ile çarparak çıkarırız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 3 & 8 & 1 & 1 \\[2ex] 6 & 4 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3 -2f_1} & \end{array} \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d68ac25745ddc71d1e7f55f68dd4ea7a_l3.png)
Ana köşegenin altındaki tüm sayılar 0 olduğunda, sistemi denklem formuna geçirmeye geri döneriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 2 & -1 & 1 \\[2ex] 0 & 6 & 2 & 0 \\[2ex] 0 & 0 & 1 & -3 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 3x+2y-z=1 \\[2ex] 6y+2z=0\\[2ex] 1z=-3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4457f1b034e72c6945bfe609eff52b9a_l3.png)
Yani bu sistem SCD’dir , çünkü matris kaydırılmıştır ve son satır şu türdendir:
![]()
. Bu nedenle, her zaman olduğu gibi çözüyoruz: denklemlerdeki bilinmeyenleri aşağıdan yukarıya doğru çıkararak.
![]()
![]()
![]()
Artık z’yi bildiğimize göre, değerini bulmak için değerini ikinci denkleme yerleştiririz.
![]()
:
![]()
![]()
![]()
![]()
![]()
Ve son olarak, ilk denklem için de aynısını yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve çözüyoruz
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Gauss yöntemine göre uyumsuz sistemler
Gauss matrisinde arka arkaya üç 0 ve bir sayı içeren bir satırımız var.
![]()
, bu bir IS (Uyumsuz Sistem) ve bu nedenle sistemin bir çözümü yok .
Örnek:
Örneğin, bir sistemin Gauss matrisiyle çalıştıktan sonra elimizde şunun kaldığını hayal edin:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & 1 & -1 & 0 \\[2ex] 0 & 3 & 1 & -1 \\[2ex] 0 & 0 & 0 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-defe65fa616eff800314ebc6dc6f552b_l3.png)
Son satır olduğu gibi
![]()
yani sonunda bir sayının geldiği üç 0 bir IF’dir (Uyumsuz Sistem) ve bu nedenle sistemin çözümü yoktur .
Bilmenize gerek olmasa da neden bir çözümü olmadığını aşağıda göreceksiniz.
Son satırı alırsak şu denklemi elde ederiz:
![]()
Bu denklem hiçbir zaman gerçekleşmeyecektir, çünkü z değeri ne olursa olsun, onu 0 ile çarpmak asla 2 vermeyecektir (herhangi bir sayının 0 ile çarpımı her zaman 0 verir). Ve bu denklem hiçbir zaman sağlanamayacağı için sistemin çözümü de yoktur.
Gauss yöntemiyle belirlenemeyen uyumlu sistemler
Gauss matrisinin bir satırı 0 ile doldurulduğunda
![]()
, bu bir SCI (Belirsiz Uyumlu Sistem) ve dolayısıyla sistemin sonsuz çözümleri var .
Bir ICS’nin nasıl çözüleceğine dair bir örnek görelim:
Örnek:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a63dfebc1f23923714e475aad2e808_l3.png)
Her zaman olduğu gibi öncelikle sistemin genişletilmiş matrisini oluşturuyoruz:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y-1z=-2 \\[2ex] 3x+4y+z=4 \end{array} \right\} \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f273040101827fdfea5c9a4858be5567_l3.png)
Şimdi ana köşegenin altındaki tüm sayıların 0 olmasını istiyoruz. Yani ikinci satıra ilk satırı -2 ile çarparak ekliyoruz:
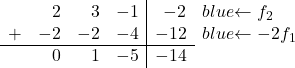
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & -1 & -2 \\[2ex] 3 & 4 & 1 & 4\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c889a6f147c6b0430731aa778121af52_l3.png)
3’ü 0’a dönüştürmek için üçüncü satıra ilk satırı -3 ile çarparak ekleriz:
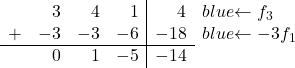
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 3 & 4 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5acccc51108267fef6d3320068743aa_l3.png)
Son satırdaki 1’i 0’a dönüştürmek için üçüncü satıra ikinci satırı -1 ile çarparak ekliyoruz:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a02e4819adfbe7b80d2952f87f113757_l3.png)
Son satırın tamamı 0 olduğundan onu kaldırabiliriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6aea469dceab08e6aa62571922eb2824_l3.png)
Ve elimizde 0’larla dolu bir satır olduğundan bu bir SCI’dır.
Bu nedenle aşağıdaki sistemi elde ediyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & -5 & -14 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y+2z=6 \\[2ex] y-5z=-14 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-598c031f4cba5a865952a57ed46f0f95_l3.png)
Sistem SCI olduğunda parametrenin değerini bilinmeyen bir yerden almak gerekir.
![]()
. Ve sistemi bu parametreye göre çözmemiz gerekiyor
![]()
.
Bu nedenle değerini atadık
![]()
z’ye :
![]()
Her ne kadar değerini almak için başka bir bilinmeyeni de seçebilirsek de
![]()
.
Şimdi y’yi ikinci denklemden ayırıyoruz ve bunun bir fonksiyonu olmasına izin veriyoruz:
![]()
:
![]()
![]()
![]()
Ve son olarak ilk denklemden x’i silip onu bir fonksiyon olarak bırakıyoruz.
![]()
:
![]()
![]()
![]()
![]()
Bu nedenle sistem çözümleri şunlardır:
![]()
Gördüğünüz gibi sistem SCI olduğunda çözümleri parametreye bağlı olarak bırakıyoruz.
![]()
. Ve sonsuz çözümü olduğunu unutmayın çünkü aldığı değere bağlı
![]()
çözüm ya biri ya da diğeri olacaktır.
Çözülmüş alıştırmalara geçmeden önce bilmelisiniz ki, bu makalede Gauss yöntemini kullansak da, doğrusal denklem sistemlerini tartışmanın ve çözmenin bir başka yolu da Rouche teoremidir . Aslında muhtemelen daha çok kullanılıyor.
Denklem sistemlerinin Gauss-Jordan yöntemi kullanılarak tartışılmasına yönelik çözülmüş alıştırmalar
1. Egzersiz
Ne tür bir sistemin söz konusu olduğunu belirleyin ve aşağıdaki denklem sistemini Gauss yöntemini kullanarak çözün:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be4ba1bd1ce7452e66c5189d995d948c_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y+2z=6 \\[2ex] 2x+3y+5z=8 \\[2ex] 3x+3y+6z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex] 3 & 3 & 6 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b600f3fc0d79a06eb972dbacb673a780_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki terimini iptal etmek için satır işlemleri gerçekleştiririz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 2 & 3 & 5 & 8 \\[2ex]3 & 3 & 6 & 9 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_1} \\[2ex] \xrightarrow{f_3 - 3f_1}& \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 2 & 6 \\[2ex] 0 & 1 & 1 & -4 \\[2ex] 0 & 0 & 0 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1d832d5bb115666614ae96822c360eb_l3.png)
Üç 0’dan ve ardından bir sayıdan oluşan bir matris satırı elde ettik. Dolayısıyla bu bir IS (Uyumsuz Sistem)’dir ve sistemin bir çözümü yoktur.
Alıştırma 2
Ne tür bir sistem olduğunu belirleyin ve Gauss yöntemini kullanarak aşağıdaki denklem sisteminin çözümünü bulun:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f5aba495f2c6a301e923ee3c6238012_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-2y+3z=1 \\[2ex] -2x+5y-z=5 \\[2ex] -x+3y+2z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8bb5e5ab85946bddad72067fe17d937_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki terimini iptal etmek için satır işlemleri gerçekleştiririz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] -2 & 5 & -1 & 5 \\[2ex] -1 & 3 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 2f_1} \\[2ex] \xrightarrow{f_3 + f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e48becaaa6683719ac57eb7d118943_l3.png)
Şimdi ikinci sütundaki son öğeyi kaldırmayı deneyelim:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-16a1afc0eb224ee5f05c9e313586854d_l3.png)
Ama tam bir 0 satırı elde ediyoruz. Yani bu bir SCI ve sistemin sonsuz sayıda çözümü var.
Ancak bu bir ICS olduğu için sistemi temel alarak çözebiliriz.
![]()
. Bu nedenle 0 satırını siliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c838c5f1b229d4c8a43ac9ddd8e3629_l3.png)
Şimdi matrisi bilinmeyenli bir denklem sistemi biçiminde ifade ediyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 0 & 1 & 5 & 7 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-2y+3z=1 \\[2ex] 1y+5z=7 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3fd941d33fec646d16b8181430c9986_l3.png)
değerini veriyoruz
![]()
İçin
![]()
![]()
değerini değiştiriyoruz
![]()
değerini bulmak için ikinci denklemde
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini değiştiriyoruz ve siliyoruz
![]()
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Alıştırma 3
Ne tür bir sistem olduğunu bulun ve aşağıdaki denklem sistemini Gauss yöntemiyle çözün:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b04370b42854e53c650ca0eae14aadb5_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 4x-4y+z=-4 \\[2ex] x+3y+z=2 \\[2ex] x+5y+2z=6\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff2c7644e19fdf405f3c5c42ffc0ee98_l3.png)
Gauss yöntemini uygulamak için ilk satırdaki ilk sayının 1 olması daha kolaydır. Bu nedenle 1 ve 2 numaralı satırların sırasını değiştireceğiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 4 & -4 & 1 & -4 \\[2ex] 1 & 3 & 1 & 2 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 \rightarrow f_2} \\[2ex] \xrightarrow{f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-471d89605d4bf6ddef1896a8fbe4c5ea_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki terimini iptal etmek için satır işlemleri gerçekleştiririz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 4 & -4 & 1 & -4 \\[2ex] 1 & 5 & 2 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 4f_1} \\[2ex] \xrightarrow{f_3 -f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f4d5cbc50b87927077018175c4678e90_l3.png)
Şimdi ikinci sütunun son elemanını sıfıra dönüştürüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 2 & 1 & 4 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{8f_3 + f_2} \end{array} \left( \begin{array}{ccc|c}1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9013720883fd719e2bd0779bfbaa7a9f_l3.png)
Bu sistem SCD’dir , çünkü matrisi kaydırmayı başardık ve son satır şu türdendir:
![]()
. Bu nedenle benzersiz bir çözüme sahip olacaktır.
Ana köşegenin altındaki tüm sayılar 0 olduğunda artık denklem sistemini çözebiliriz. Bunu yapmak için matrisi tekrar bilinmeyenli bir denklem sistemi biçiminde ifade ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 1 & 2 \\[2ex] 0 & -16 & -3 & -12 \\[2ex] 0 & 0 & 5 & 20 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+1z=2 \\[2ex] -16y-3z=-12 \\[2ex] 5z=20 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0f0433738d5d0a22bdd3b04dbd44fd1e_l3.png)
Ve denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözüyoruz. İlk önce son denklemi çözüyoruz:
![]()
![]()
Şimdi y’nin değerini bulmak için z’nin değerini ikinci denklemde yerine koyacağız:
![]()
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve x’i çözüyoruz:
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Alıştırma 4
Ne tür bir sistem olduğunu belirleyin ve aşağıdaki denklem sistemini Gauss yöntemiyle çözün:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e8a133547b4719d7833a792550fd322_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x-y+4z=2 \\[2ex] -3x-3y+3z=7 \\[2ex] -2x-4y+7z=9 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc41f78456a922a0fbff419d336b0b46_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki terimini iptal etmek için satır işlemleri gerçekleştiririz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] -3 & -3 & 3 & 7 \\[2ex] -2 & -4 & 7 & 9\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 3f_1} \\[2ex] \xrightarrow{f_3 + 2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff92912f653c6aca7ceb7c990c9635a3_l3.png)
Şimdi ikinci sütundaki son öğeyi kaldırmayı deneyelim:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & -6 & 15 & 13\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -1f_2} \end{array} \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c6904a64a721f3a92bef8c6b7d713cf_l3.png)
Ama tam bir 0 satırı elde ediyoruz. Yani bu bir SCI ve sistemin sonsuz sayıda çözümü var.
Ancak bu bir ICS olduğu için sistemi temel alarak çözebiliriz.
![]()
. Bu nedenle 0 satırını siliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13\\[2ex] 0 & 0 & 0 & 0 \end{array} \right) \ \longrightarrow \ \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d856e2c1246f3629d68a7bcd3cd759a_l3.png)
Şimdi matrisi bilinmeyenli bir denklem sistemi biçiminde ifade ediyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -1 & 4 & 2 \\[2ex] 0 & -6 & 15 & 13 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x-1y+4z=2 \\[2ex] -6y+15z=13 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4cf1265bfc12f94580de183230c8b7c_l3.png)
değerini veriyoruz
![]()
İçin
![]()
![]()
değerini değiştiriyoruz
![]()
değerini bulmak için ikinci denklemde
![]()
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini değiştiriyoruz ve siliyoruz
![]()
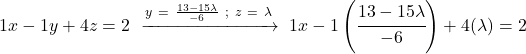
![]()
![]()
Kesirli bir toplamımız var. Bu nedenle tüm terimleri ortak bir paydaya indiriyoruz:
![]()
![]()
Artık hepsi aynı paydaya sahip olduğundan, bunları tek bir kesir halinde gruplandırabiliriz:
![]()
Ve son olarak pay üzerinde işlem yapıyoruz:
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()