Bu sayfada Gauss-Jordan yönteminin ne olduğunu ve Gauss yöntemini kullanarak bir denklem sisteminin nasıl çözüleceğini öğreneceksiniz. Ayrıca Gauss yöntemine sahip sistemlerin örneklerini ve çözülmüş alıştırmalarını da bulacaksınız, böylece onu mükemmel bir şekilde uygulayabilir ve anlayabilirsiniz.
Gauss’un yöntemi nedir?
Gauss-Jordan yöntemi, 3 bilinmeyenli denklem sistemlerini çözmek için kullanılan bir prosedürdür, yani şu şekildedir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-088146ef83bbd007e82aca8189434c25_l3.png)
Gauss yönteminin amacı, başlangıçtaki denklem sistemini kademeli bir sisteme , yani her denklemin bir öncekinden daha az bilinmeyene sahip olduğu bir sisteme dönüştürmektir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10926b0856ae512c737ae924bd9413a1_l3.png)
Ancak bunu yapabilmek için öncelikle bir denklem sistemini matris formunda nasıl ifade edeceğinizi ve bu matriste izin verilen dönüşümleri bilmeniz gerekir. Bu yüzden önce bu iki şeyi açıklayacağız, ardından Gauss yöntemi prosedürünün nasıl kullanılacağını göreceğiz.
Sistem genişletilmiş matris
Sistemin nasıl çözüldüğünü görmeden önce, bir denklem sisteminin bir matris biçiminde ifade edilebileceğini bilmelisiniz:
![]()
Birinci sütuna katsayılar yazılır.
![]()
ikinci sütunda katsayılar
![]()
üçüncü sütunda, bilinmeyen olmayan sayılar ise dördüncü sütunda yer almaktadır.
Örneğin:
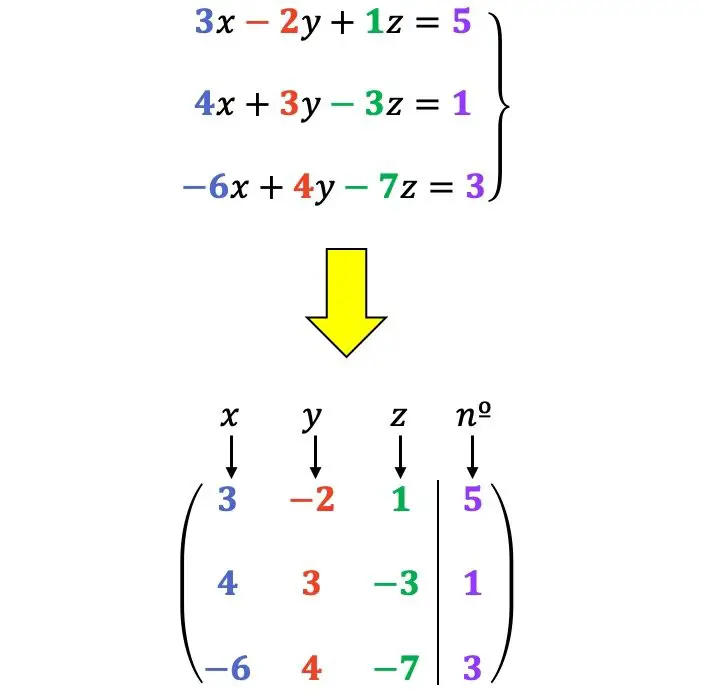
İzin verilen satır dönüşümleri
Denklem sistemini ölçekli sisteme dönüştürmek için sisteme ait matris üzerinde aşağıdaki işlemlerden biri yapılabilir:
- Matristeki satırların sırasını değiştirin .
Örneğin bir matrisin 2. ve 3. satırlarının sırasını değiştirebiliriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ee0e251559ef9dfd02c9b0105f934af8_l3.png)
- Bir satırdaki tüm terimleri 0’dan farklı bir sayıyla çarpın veya bölün .
Örneğin 1. satırı 4 ile çarpabilir ve 3. satırı 2’ye bölebiliriz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e1f081c9056075ede064b2e5c9e4193_l3.png)
- Bir satırı, aynı satırın toplamı artı başka bir satırın bir sayıyla çarpılmasıyla değiştirin .
Örneğin, aşağıdaki matriste 2. satırı 3. satıra 1 ile çarparak ekliyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-04417e2094ac05c7a374334c55197f36_l3.png)
Gauss yöntemini kullanarak bir denklem sistemi nasıl çözülür?
Şimdi bir örnek üzerinden bir denklem sistemini Gauss yöntemiyle çözme prosedürünü göreceğiz:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e6e829301e6730c9e27f9c0a30de2e_l3.png)
Yapılacak ilk şey sistemin genişletilmiş matrisidir :
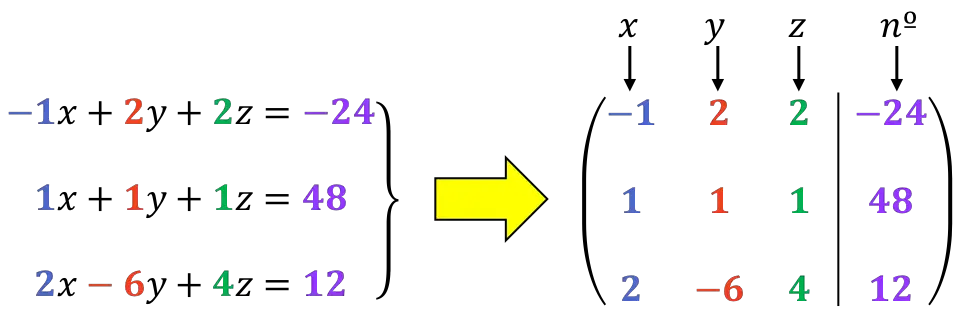
Daha sonra göreceğimiz gibi, ilk satırın ilk rakamının 1 olması daha iyidir. Bu nedenle 1. ve 2. satırların sırasını değiştireceğiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b45e0f757ca2880442314f6a4800697b_l3.png)
Gauss yönteminin amacı ana köşegenin altındaki sayıları 0 yapmaktır . Yani kırmızı sayıları 0’a dönüştürmemiz gerekiyor:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-28164ac6b48d32c09b4725548c0633f6_l3.png)
Bu sayıları ortadan kaldırmak için satırlarda uygun dönüşümleri yapmamız gerekiyor.
Örneğin ikinci satırın ilk elemanı olan -1, birinci satırın ilk elemanı olan 1’in negatifidir. Dolayısıyla ilk satırı ikinci satıra eklersek -1 ortadan kalkacaktır:

Yani bu toplamı yaparsak aşağıdaki matrisi elde ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b106306b92bfc3e99d602c22d5198bd_l3.png)
Bu şekilde -1’i 0’a dönüştürmeyi başardık.
Şimdi 2’yi dönüştüreceğiz. Dikkat ederseniz üçüncü satırın ilk elemanı olan 2, birinci satırın ilk elemanı olan 1’in iki katıdır. Dolayısıyla ilk satırı -2 ile çarparak üçüncü satıra eklersek 2 elenir:
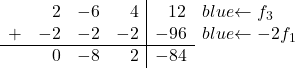
Bu nedenle aşağıdaki matrisi elde ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-36b2fdf8de855cf35049ecefcf7c1da5_l3.png)
Bu şekilde 2’yi 0’a dönüştürmeyi başardık.
Şimdi tek yapmamız gereken -8’i 0’a çevirmek. Bunu yapmak için üçüncü satırı 3 ile çarpıyoruz ve ikinci satırı 8 ile çarpıyoruz:
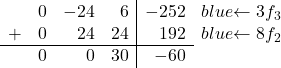
Dolayısıyla aşağıdaki matrisi elde ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e2324629222c746a9021ce05ba7d54d_l3.png)
Ve bu dönüşümlerle ana köşegenin altındaki tüm sayıların 0 olmasını sağladık. Artık denklem sistemini çözebiliriz.
Şimdi matrisi bilinmeyenli bir denklem sistemine dönüştürmeliyiz . Bunu yapmak için ilk sütunun şuna karşılık geldiğini unutmayın:
![]()
, ikinci sütunu
![]()
, üçüncü sütunu
![]()
ve son sütun bilinmeyen olmayan sayılardır:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f90de9d9f5a06959a2d4aebf05f4758_l3.png)
Ve son olarak sistemi çözmek için denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözmemiz gerekiyor. Son denklemin yalnızca bir bilinmeyeni olduğundan onu çözebilir ve değerini bulabiliriz:
![]()
![]()
![]()
Artık z’nin ne olduğunu bildiğimize göre, değerini ikinci denklemde yerine koyarsak, z’nin değerini bulabiliriz.
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini değiştiriyoruz ve siliyoruz
![]()
:
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Denklem sistemi problemlerinin Gauss-Jordan yöntemiyle çözülmesi
1. Egzersiz
Aşağıdaki denklem sistemini Gauss yöntemini kullanarak çözün:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854043b0e7e3e2166593dcf5c645bfa0_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b6369a58b91f31bf4c8bc212ccf68c6_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki terimini iptal etmek için satır işlemleri gerçekleştiririz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd42dcf61aebc4c67de13e09dff72f4b_l3.png)
Şimdi ikinci sütundaki son öğeyi kaldırıyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-13945337848a6f1badf6efe249951124_l3.png)
Ana köşegenin altındaki tüm sayılar 0 olduğunda artık denklem sistemini çözebiliriz. Bunu yapmak için matrisi tekrar bilinmeyenli bir denklem sistemi biçiminde ifade ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f068c276aae018a668cc005bcad3e641_l3.png)
Ve denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözüyoruz. İlk önce son denklemi çözüyoruz:
![]()
![]()
Şimdi y’nin değerini bulmak için z’nin değerini ikinci denklemde yerine koyacağız:
![]()
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve x’i çözüyoruz:
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Alıştırma 2
Gauss yöntemini kullanarak aşağıdaki denklem sisteminin çözümünü bulun:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0595899b8137f769c74fce1b21286b_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e2a16b6d1451520bd8898675c022dc2_l3.png)
Gauss yöntemini uygulamak için ilk satırdaki ilk sayının 1 olması daha kolaydır. Bu nedenle 1 ve 2 numaralı satırların sırasını değiştireceğiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef7e2e42d0eecb0395afb7c8311b2ade_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki öğesini değiştirmek için satır işlemleri gerçekleştiriyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-40baaee3bbde9ed1577e00bc1c3b338f_l3.png)
Şimdi ikinci sütunun son elemanını sıfıra dönüştürüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f328906485bfe6ee77833c04869e1240_l3.png)
Ana köşegenin altındaki tüm sayılar 0 olduğunda denklem sistemini çözebiliriz. Bunu yapmak için matrisi tekrar bilinmeyenli bir denklem sistemi biçiminde ifade ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7e129715c720218a5cb25ef07442442_l3.png)
Ve denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözüyoruz. İlk önce son denklemi çözüyoruz:
![]()
![]()
Şimdi y’nin değerini bulmak için z’nin değerini ikinci denklemde yerine koyacağız:
![]()
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve x’i çözüyoruz:
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Alıştırma 3
Aşağıdaki denklem sisteminin çözümünü Gauss yöntemiyle hesaplayın:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4301eae3179543fbdee7568e8f88aa4c_l3.png)
Yapmamız gereken ilk şey sistemin genişletilmiş matrisidir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0d96160d6670e817dd39f61816e1e6e_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki öğesini değiştirmek için satır işlemleri gerçekleştiriyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-87853177b6be449178c24e414dc0865a_l3.png)
Şimdi ikinci sütunun son elemanını sıfıra dönüştürüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4105ceb64b201c532109f8639bdefde_l3.png)
Ana köşegenin altındaki tüm sayılar 0 olduğunda denklem sistemini çözebiliriz. Bunu yapmak için matrisi tekrar bilinmeyenli bir denklem sistemi biçiminde ifade ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-faae83295a3f7b3d8b6d76f78d56fac6_l3.png)
Ve denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözüyoruz. İlk önce son denklemi çözüyoruz:
![]()
![]()
Şimdi y’nin değerini bulmak için z’nin değerini ikinci denklemde yerine koyacağız:
![]()
![]()
![]()
![]()
Aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve x’i çözüyoruz:
![]()
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()
Alıştırma 4
Aşağıdaki 3 bilinmeyenli denklem sistemini Gauss yöntemini kullanarak çözün:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b005b2eda0d63c7130f2f5531c2ae4a0_l3.png)
Gauss yöntemini uygulamadan önce denklem sistemini, tüm bilinmeyenler denklemin solunda ve sayılar sağda olacak şekilde düzenlememiz gerekir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0ca77b625e8f9e235ce8da4e4008df_l3.png)
Sistem sipariş edildikten sonra sistemin geliştirilmiş matrisini oluştururuz:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b88e3ff141b847028a55ba4b46b8e870_l3.png)
İlk satırdaki tüm sayılar çift olduğundan satırlarla işlem yapmadan önce ilk satırı 2’ye böleceğiz. Bu hesaplamaları kolaylaştıracağından:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05235526cd8e44c16749606bfe8976c_l3.png)
Şimdi ana dizinin altındaki tüm sayıları 0 yapmamız gerekiyor.
Bu nedenle, ilk sütunun son iki öğesini değiştirmek için satır işlemleri gerçekleştiriyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3da82815d14fdfae0f61a8e1747fb9fe_l3.png)
Daha önce olduğu gibi son satırdaki sayıların tümü 9’un katı olduğundan hesaplamaları kolaylaştırmak için bunu 9’a böleceğiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-342000d19a7bd19e055a39695c79cb49_l3.png)
Şimdi ikinci sütunun son elemanını sıfıra dönüştürüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2158e7f439f677617bb8a40695fb5711_l3.png)
Ana köşegenin altındaki tüm sayılar 0 olduğunda denklem sistemini çözebiliriz. Bunu yapmak için matrisi tekrar bilinmeyenli bir denklem sistemi biçiminde ifade ederiz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ea162e98aa70f8d56ffba28438a9de2a_l3.png)
Ve denklemlerin bilinmeyenlerini aşağıdan yukarıya doğru çözüyoruz. İlk önce son denklemi çözüyoruz:
![]()
![]()
Şimdi y’nin değerini bulmak için z’nin değerini ikinci denklemde yerine koyarız:
![]()
![]()
![]()
![]()
![]()
Ve aynısını ilk denklem için de yapıyoruz: diğer bilinmeyenlerin değerlerini yerine koyuyoruz ve x’i çözüyoruz:
![]()
![]()
![]()
![]()
Bu nedenle denklem sisteminin çözümü şu şekildedir:
![]()