Belirleyicilerin özellikleri

Bu bölümde determinantların tüm özelliklerinin ne olduğunu göreceğiz. Ayrıca her özelliği bir örnekle gösteriyoruz, böylece onları tam olarak anlayabilirsiniz. Ayrıca belirleyicilerin özelliklerine ilişkin alıştırmalar da bulacaksınız.

Aşağıda determinantların her bir özelliğini tek tek açıklayacağız ancak isterseniz doğrudan aşağıdaki özet tablosuna geçebilirsiniz. 😉

Özellik 1: Yer değiştiren matrisin determinantı

Bir matrisin determinantı, aktarılan matrisinin determinantına eşdeğerdir.

\lvert A \rvert = \lvert A^t \rvert

Örnek:

\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}

Şimdi 2×2’lik matrisin devriğini değiştirip determinantı çözüyoruz. Öncekiyle aynı sonucu elde ettiğimize dikkat edin:

\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}

Özellik 2: Satırı veya sütunu sıfırlarla dolu olan determinant

Bir determinantın sıfırlarla dolu bir satırı veya sütunu varsa determinant 0 değerini döndürür.

\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0

Örnek:

\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}

Bu örneklerin her ikisinde de determinantlar 0 olarak değerlendirilir. Çünkü birinci determinantın ikinci satırının tamamı sıfırdır ve ikinci determinantın üçüncü sütununun tamamı da sıfırdır.

Özellik 3: İki eşit satır veya sütuna sahip determinant

Bir determinantın iki eşit veya çoklu satırı veya iki sütunu varsa determinant sıfırdır (0).

Dolayısıyla satırlar veya sütunlar arasında doğrusal bir kombinasyon varsa, yani doğrusal bağımlıysa determinant 0 verir.

Örnek:

\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0

Bu durumda 2 ve 3 numaralı sütunlar eşit olduğundan determinant 0 verir.

Özellik 4: Bir determinantın satırlarını veya sütunlarını değiştirme

İki satır veya iki sütun birbirine göre değiştirilirse determinant aynı sonucu verir ancak farklı bir işaretle.

\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}

Örnek:

\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}

Şimdi 2. ve 3. sütunların sırasını birbirine göre değiştiriyoruz. Sonucun aynı olduğunu ancak farklı bir işarete sahip olduğunu unutmayın:

\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}

Özellik 5: Bir determinantın satırını bir skalerle çarpma

Bir satır veya sütunun tamamındaki tüm öğeleri bir gerçek sayıyla çarpmak, determinantın sonucunu bu sayıyla çarpmakla aynıdır.

\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}

Örnek:

\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}

Şimdi aynı determinantı alıyoruz ve tüm doğruyu 2 ile çarpıyoruz. Sonucun önceki determinantın sonucu olacağını ancak 2 veya 10 ile çarpıldığını göreceksiniz:

\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}

Özellik 6: Matris çarpımının determinantı

İki matrisin çarpımının determinantı, her matrisin determinantının ayrı ayrı çarpımına eşittir.

\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert

Örnek:

Determinantların bu özelliğini göstermek için aşağıdaki iki matrisin çarpımının determinantını iki olası yolla hesaplayacağız:

\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}

Önce iki matrisi çarpacağız, sonra elde edilen matrisin determinantını hesaplayacağız:

\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}

Şimdi her matrisin determinantını ayrı ayrı hesaplayıp sonuçları çarpıyoruz:

\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}

Gördüğünüz gibi, önce matris çarpımını, sonra determinantı yapmak, her matrisin önce determinantını yapıp sonra sonuçları çarpmakla aynı sonucu verir.

Öte yandan, bu koşul toplama ve çıkarma işlemleri için geçerli değildir, yani iki matrisin toplanmasının (veya çıkarılmasının) determinantı, matrislerin determinantlarının toplanması (veya çıkarılması) ile aynı sonucu vermez. iki matris ayrı ayrı.

Özellik 7: Ters matrisin determinantı

Bir matris tersinirse, tersinin determinantı, orijinal matrisin determinantının tersine karşılık gelir.

\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}

Örnek:

Bu özelliği önce bir matrisin tersini hesaplayıp ardından determinantını çözerek doğrulayacağız. Sonucun orijinal matrisin determinantını bulup tersine çevirmeye eşdeğer olduğunu göreceğiz.

Bu nedenle aşağıdaki matrisi ters çevirip determinantını hesaplıyoruz:

\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}

\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}

\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}

Şimdi orijinal matrisin determinantını çözüyoruz ve bunun tersini yapıyoruz:

\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2

\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}

Gördüğünüz gibi her iki operasyonun sonuçları da aynı. Bu nedenle mülkiyet kanıtlanmıştır.

Özellik 8: Belirleyicinin çizgisini değiştirin

Bir determinantın satırı, aynı satırın artı (veya eksi) başka bir satırın bir sayıyla çarpılmasıyla (veya çıkarılarak) değiştirilebilir.

Örnek:

Aşağıdaki örnekte bu özelliği kontrol edeceğiz. Önce bir determinant hesaplayacağız, sonra determinantın bir satırı üzerinde işlem yapıp sonucunu yeniden hesaplayacağız. Her iki durumda da aynı sonucu nasıl elde ettiğimizi göreceksiniz.

O halde önce Sarrus kuralıyla 3×3’lük bir determinantı hesaplayalım:

\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}

Şimdi 2. satıra ilk satırı 2 ile çarparak ekliyoruz:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}

Ve determinantı, çizgilerinden birini dönüştürdükten sonra çözüyoruz:

\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}

Her iki durumda da sonuç -3 oldu. Böylece, bir satırın yerine aynı satırın toplamı artı başka bir satırın bir sayıyla çarpılması durumunda determinantın sonucunun değişmediği gösterilmiştir.

Özellik 9: Üçgensel bir matrisin determinantı

Üçgen bir matrisin determinantı, ana köşegeninin elemanlarının çarpımıdır.

Örnek:

Örnek olarak aşağıdaki üçgen matrisin determinantını çözeceğiz:

\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}

Özellik 10: Köşegen matrisin determinantı

Köşegen bir matrisin determinantı, ana köşegeninin elemanlarının çarpımına eşittir.

Örnek:

Örnek olarak aşağıdaki köşegen matrisin determinantını ele alalım:

\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}

Belirleyicilerin özelliklerinin özet tablosu

Açıklanan belirleyicilerin özellikleri aşağıdaki tabloda özetlenebilir:

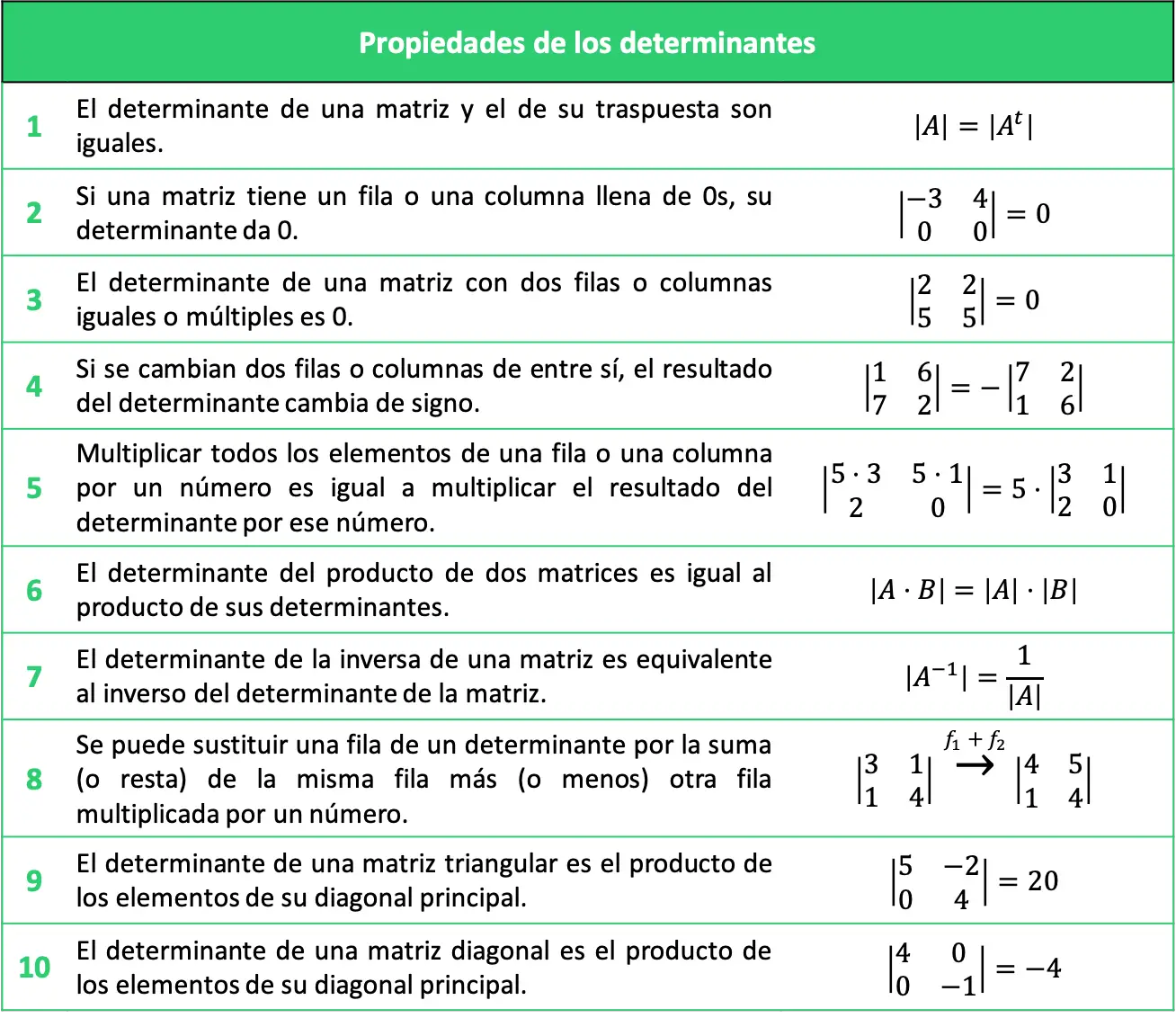
belirleyicilerin özellikleri

Belirleyicilerin özellikleriyle çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki determinantı çözün:

\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}

Bir determinantın sıfırlarla dolu bir satırı veya sütunu varsa determinant 0 değerini döndürür (özellik 2). Bu nedenle üçüncü sütun sıfırlarla dolu olduğundan determinantın sonucu 0’dır.

Alıştırma 2

Aşağıdaki determinantı çözün:

\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}

Bir determinantın iki eşit veya birden fazla satırı veya iki sütunu varsa, determinant 0 değerini döndürür (özellik 3). Dolayısıyla birinci satır ile üçüncü satır eşit olduğundan determinantın sonucu 0 olur.

Alıştırma 3

Aşağıdaki determinantı hesaplayın:

\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}

Bir determinantın iki eşit veya birden fazla satırı veya iki sütunu varsa, determinant 0 değerini döndürür (özellik 3). Bu nedenle determinantın sonucu 0’dır çünkü dördüncü sütun birinci sütunun iki katıdır.

Alıştırma 4

Matrisin elemanlarını bilmesek de determinantın sonucunu biliyoruz:

\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3

Önceki determinantın sonucundan ve determinantların özelliklerinden aşağıdaki determinantların sonucunu hesaplayın:

\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}

İçin)

\begin{pmatrix} a & c \\ b & d \end{pmatrix}

transpoze matrisidir

\begin{pmatrix} a & b \\ c & d \end{pmatrix}

. Ve bir matrisin determinantı, aktarılan matrisinin (özellik 1) determinantına eşittir. Dolayısıyla bu determinantın sonucu da 3’tür.

\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}

b) Belirlemede

\begin{vmatrix} b & a \\ d & c \end{vmatrix}

1. ve 2. sütunlar ifadenin belirleyicisine göre değiştirildi

\begin{vmatrix} a & b \\ c & d \end{vmatrix}

. Dolayısıyla özellik 4’e göre sonuç, ifadenin belirleyicisinin sonucuyla aynı ancak farklı bir işaretle yani -3 olur.

\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}

c) Belirlemede

\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}

ifadenin determinantının ikinci sütununun tamamı 3 ile çarpılmıştır. Bu nedenle, 5 özelliğinden , sonucunun aynı zamanda ifadenin determinantının 3, yani 9 ile çarpılmasının sonucu olacağı sonucunu çıkarabiliriz.

\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}

Alıştırma 5

Bu iki belirleyicinin sonucunu biliyoruz:

\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8

\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4

Bu bilgilere göre şunu hesaplayın:

\displaystyle \vert A \cdot B \vert

Determinantın sonucunu hesaplamak için 4×4 matrisleri çarpmaya gerek yoktur. Çünkü iki matrisin çarpımının determinantı, her matrisin determinantının ayrı ayrı çarpımına eşittir (özellik 6). Henüz:

\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top