Bu sayfada 3×3 kare matrisin determinantının ne olduğunu öğreneceksiniz. Sarrus kuralını kullanarak 3. dereceden determinantları nasıl çözeceğinizi göreceksiniz. Ayrıca adım adım çözülmüş örnekler ve alıştırmalar da var, böylece pratik yapabilir ve mükemmel bir şekilde anlayabilirsiniz.
3×3’lük bir matrisin determinantı nedir?
3. dereceden bir determinant, matrisin her iki tarafında dikey bir çubukla temsil edilen 3×3 boyutlu bir matristir. Örneğin aşağıdaki matrise sahipsek:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b5e89b706893e88dd15882e3685afb1_l3.png)
A matrisinin determinantı aşağıdaki gibi temsil edilir:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41db04327de87a80f1e0e4dd6dcb220a_l3.png)
Gördüğünüz gibi 3. mertebeden bir kare matrisin determinantını yazmak kolaydır. Şimdi bunu nasıl çözeceğimize bakalım:
3. dereceden bir determinant nasıl hesaplanır?
3×3 matrislerin determinantlarını oluşturmak için Sarrus kuralını uygulamanız gerekir:
Sarrus kuralı
Sarrus kuralı, 3. dereceden bir determinantı hesaplamak için, büyük köşegenin elemanlarının çarpımını ve paralel köşegenlerinin çarpımını karşılık gelen zıt köşelerle toplamamız, ardından küçük köşegenin elemanlarının çarpımını çıkarmamız gerektiğini söylüyor ve paralel köşegenlerinin karşılık gelen zıt köşeleriyle çarpımı.
Bu şekilde yazınca anlaşılması biraz zor olabilir ama 3×3 determinant hesaplamasının nasıl yapıldığına aşağıdaki diyagram ve örneklerle bakın:


3×3 determinant örnekleri:
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98e60cf465cd0eb7662d47770cd38231_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41a53c1fd6eae1b51a280a6ce1e2ab91_l3.png)
3 × 3 matrislerin determinantlarının çözülmüş problemleri
1. Egzersiz
Aşağıdaki 3×3 determinantını çözün:
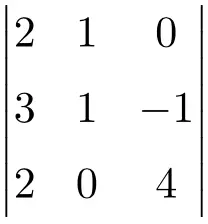
3×3’lük bir matrisin determinantını çözmek için Sarrus kuralını uygulamalıyız:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f288312b72f3bbabc35ee64bf580d8c_l3.png)
Alıştırma 2
3. dereceden aşağıdaki determinantı hesaplayın:
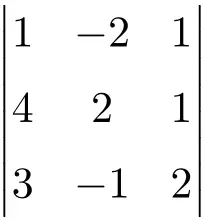
Üçüncü dereceden bir matrisin determinantını hesaplamak için Sarrus kuralını kullanmalıyız:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-64078968233ec50d2e793309d55e55fc_l3.png)
Alıştırma 3
Aşağıdaki 3×3 matrisin determinantının çözümünü bulun:
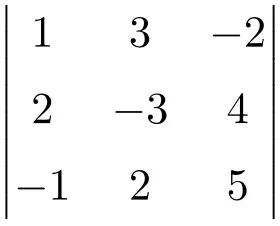
3×3’lük bir matrisin determinantını oluşturmak için Sarrus kuralını kullanmalıyız:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd4494ae66a604834b8f9f47fcbbe41d_l3.png)
Alıştırma 4
Aşağıdaki 3. mertebeden matrisin determinantının çözümünü bulun:
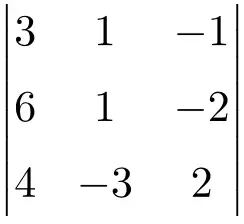
3×3’lük bir matrisin determinantının çözümünü bulmak için Sarrus formülünü uygulamalıyız:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e811024d460a60a1df59983b1f700e8_l3.png)
Alıştırma 5
değerini bul
![]()
aşağıdaki üçüncü dereceden determinantı iptal eder:
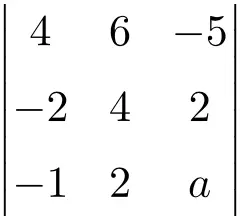
İlk önce Sarrus kuralıyla determinantın değerini aşağıdakinin bir fonksiyonu olarak hesaplıyoruz:
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07e67cfc5e45c0a11c35d643cd4c1c78_l3.png)
Determinantın ortadan kalkması için sonucun 0 olması gerekir. Bu nedenle sonucu 0’a eşitleyip denklemi çözüyoruz:
![]()
![]()
![]()