2×2'lik bir matrisin determinantı nasıl hesaplanır

Bu sayfada 2×2’lik bir matrisin determinantının ne olduğunu öğreneceksiniz. Ek olarak, 2. dereceden determinantların nasıl çözüleceğine ilişkin adım adım çözülmüş örnekler ve alıştırmalar bulacaksınız, böylece bunu mükemmel bir şekilde uygulayabilir ve anlayabilirsiniz.

2×2 determinant nedir?

2. dereceden bir determinant, matrisin her iki tarafında dikey bir çubukla temsil edilen 2 × 2 boyutlu bir matristir. Örneğin aşağıdaki matrise sahipsek:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

A matrisinin determinantı aşağıdaki gibi temsil edilir:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Gördüğünüz gibi 2×2 kare matrisin determinantını yazmak kolaydır. Şimdi nasıl hesaplandığına bakalım:

2. dereceden bir determinant nasıl çözülür?

2×2’lik bir matrisin determinantını hesaplamak için ana köşegenin elemanlarını çarpmamız ve ikincil köşegenin çarpımını çıkarmamız gerekir.

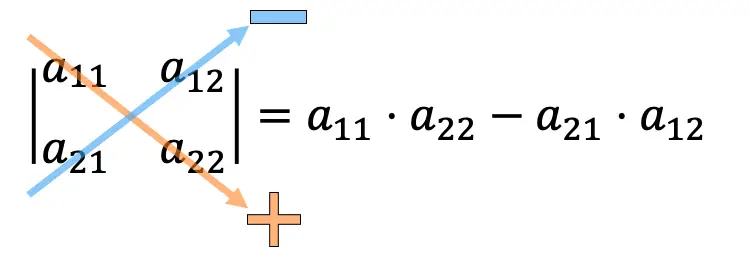
2x2'lik bir matrisin determinantını hesaplama örneği

2×2 determinantların hesaplanmasına örnekler:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

2 × 2 matrislerin determinantlarının çözülmüş problemleri

1. Egzersiz

Aşağıdaki 2×2 determinantını hesaplayın:

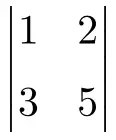
determinant 2x2'nin adım adım çözülmesi alıştırması

2×2 determinantı yapmak için ana köşegenin elemanlarını çarpmanız ve ikincil köşegenin çarpımını çıkarmanız gerekir:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

Alıştırma 2

2×2 boyutunun aşağıdaki determinantını çözün:

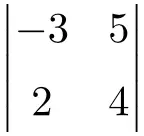
2x2 determinantlarla ilgili adım adım çözülen alıştırmalar

2. dereceden bir determinantın çözümünü bulmak için ana köşegenin elemanlarını çarpmanız ve ikincil köşegenin çarpımını çıkarmanız gerekir:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

Alıştırma 3

Aşağıdaki 2. dereceden determinantın çözümünü bulun:

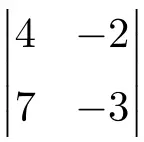
2x2'lik bir matrisin determinantının adım adım çözülmesi alıştırması

2. boyutun determinantının çözümünü bulmak için ana köşegenin elemanlarını çarpmanız ve ikincil köşegenin çarpımını çıkarmanız gerekir:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

Alıştırma 4

Aşağıdaki 2×2 determinantını hesaplayın:

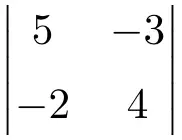
2x2'lik bir matrisin determinantı nasıl çözülür, adım adım çözülen alıştırma

2×2 matrislerin determinantlarını hesaplamak için ana köşegenin elemanlarını çarpmamız ve ikincil köşegenin çarpımını çıkarmamız gerekir:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

Alıştırma 5

Aşağıdaki 2×2 determinantının sonucunu belirleyin:

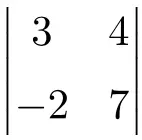
2. dereceden bir matrisin determinantının adım adım çözümüne ilişkin çözülmüş alıştırma

2×2’lik bir determinantın çözümünü bulmak için ana köşegenin elemanlarını çarpmamız ve ikincil köşegenin çarpımını çıkarmamız gerekir:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

Parlak! Artık 2×2 boyutunun determinantlarını nasıl oluşturacağınızı biliyorsunuz! Artık 3×3 determinantının nasıl hesaplandığını ve ayrıca 4×4 matrisinin determinantının nasıl çözüldüğünü kesinlikle anlayabilirsiniz.

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top