Matris çarpımı - Mathority

Bu sayfada 2×2, 3×3, 4×4 vb. boyutlardaki matrislerin nasıl çarpılacağını göreceğiz. Matris çarpma işlemini adım adım bir örnekle açıklıyoruz, ardından pratik yapabilmeniz için çözümlü alıştırmalar bulacaksınız. Son olarak iki matrisin ne zaman çarpılamayacağını ve bu matris işleminin tüm özelliklerini öğreneceksiniz.

İki matris nasıl çarpılır?

İki matrisin çarpımını gerçekleştirme prosedürünü bir örnekle görelim:

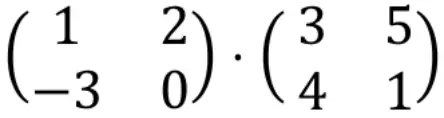
Matris çarpımını hesaplamak için soldaki matrisin satırları sağdaki matrisin sütunlarıyla çarpılmalıdır.

Bu yüzden ilk önce ilk satırı ilk sütunla çarpmamız gerekiyor. Bunun için ilk satırdaki her bir elemanı ilk sütundaki her bir elemanla tek tek çarpıyoruz ve sonuçları topluyoruz. Yani bunların hepsi ortaya çıkan dizinin ilk satırının ilk elemanı olacak. Prosedüre bakın:

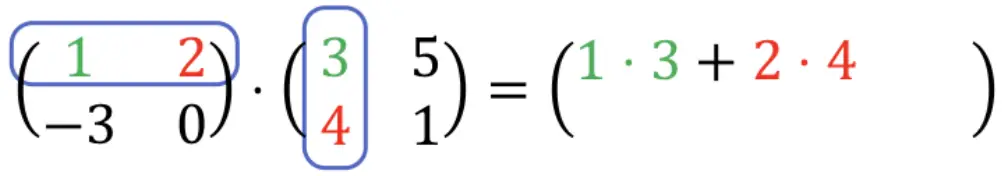
2x2 matris çarpımı, matrislerle işlemler nasıl çözülür

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Yani:

Şimdi ilk satırı ikinci sütunla çarpmamız gerekiyor. Bu nedenle işlemi tekrarlıyoruz: İlk satırın her elemanını ikinci sütunun her elemanıyla birer birer çarpıyoruz ve sonuçları topluyoruz. Ve bunların hepsi, ortaya çıkan dizinin ilk satırının ikinci elemanı olacak:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Yani:

Ortaya çıkan matrisin ilk satırını doldurduktan sonra ikinci satıra geçiyoruz. Bu nedenle prosedürü tekrarlayarak ikinci satırı birinci sütunla çarpıyoruz: ikinci satırın her bir öğesini birinci sütunun her bir öğesiyle birer birer çarpıyoruz ve sonuçları topluyoruz:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Henüz:

Son olarak ikinci satırı ikinci sütunla çarpıyoruz. Her zaman aynı prosedürle: İkinci satırın her elemanını ikinci sütunun her elemanıyla birer birer çarpıyoruz ve sonuçları topluyoruz:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Henüz:

Ve burada iki matrisin çarpımı sona eriyor. Gördüğünüz gibi, her zaman aynı işlemi tekrarlayarak satırları sütunlarla çarpmanız gerekir: satırın her öğesini sütunun her öğesiyle birer birer çarpın ve sonuçları ekleyin.

Çözülmüş matris çarpım alıştırmaları

1. Egzersiz

Aşağıdaki matris çarpımını çözün:

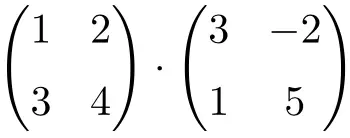
2x2 matrislerin çarpımı, matrislerle işlemler adım adım çözüldü

Çözüme bakın

2. dereceden matrislerin çarpımıdır:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

Bir matris çarpımını çözmek için soldaki matrisin satırlarını sağdaki matrisin sütunlarıyla çarpmanız gerekir.

Bu yüzden ilk önce ilk satırı ilk sütunla çarpıyoruz. Bunun için ilk satırdaki her bir elemanı ilk sütundaki her bir elemanla tek tek çarpıyoruz ve sonuçları topluyoruz. Ve bunların hepsi ortaya çıkan dizinin ilk satırının ilk elemanı olacak:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Şimdi elde edilen matrisin ilk satırının ikinci elemanını elde etmek için ilk satırı ikinci sütunla çarpalım:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

İkinci satıra geçiyoruz, böylece ikinci satırı birinci sütunla çarpıyoruz:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Son olarak, tablonun son öğesini hesaplamak için ikinci satırı ikinci sütunla çarpıyoruz:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

Yani matris çarpımının sonucu:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Alıştırma 2

Aşağıdaki 2×2 kare matris çarpımının sonucunu bulun:

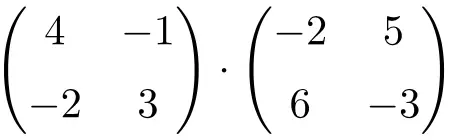
2x2 matris çarpımı, matris işlemleri konusunda adım adım çözülen alıştırma

Çözüme bakın

2×2 boyutlu matrislerin çarpımıdır.

Çarpmayı çözmek için soldaki matrisin satırlarını sağdaki matrisin sütunlarıyla çarpmanız gerekir:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Alıştırma 3

Aşağıdaki 3×3 matris çarpımını hesaplayın:

Çözüme bakın

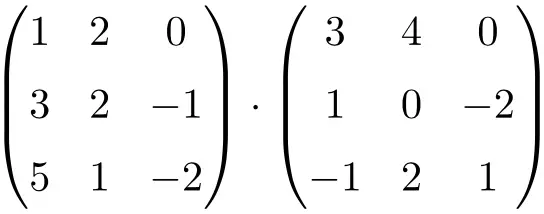
3×3 matris çarpımı yapmak için soldaki matrisin satırlarını sağdaki matrisin sütunlarıyla çarpmanız gerekir:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Alıştırma 4

matris verildiğinde

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Hesaplamak:

$\displaystyle 2A\cdot A^t$

Çözüme bakın

İlk önce devrik matrisi hesaplayacağız

$A$

çarpma işlemini yapmak için. Ve devrik matrisi oluşturmak için satırları sütunlara dönüştürmemiz gerekiyor. Yani matrisin ilk satırı matrisin ilk sütunu, ikinci satırı da matrisin ikinci sütunu olur. Henüz:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Bu nedenle matris işlemi şu şekilde kalır:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Artık hesaplamaları yapabiliriz. İlk önce hesaplıyoruz

$2A$

(her ne kadar ilk önce hesaplayabilsek de

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Ve son olarak matrislerin çarpımını çözüyoruz:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Alıştırma 5

Aşağıdaki matrisleri göz önünde bulundurun:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Hesaplamak:

$\displaystyle A\cdot B - B \cdot A$

çözümü gör

Çıkarma işlemini 2. dereceden matris çarpımlarıyla birleştiren bir işlemdir:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

İlk önce soldaki çarpımı hesaplıyoruz:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Şimdi sağdaki çarpma işlemini çözüyoruz:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

Ve son olarak matrisleri çıkarıyoruz:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

İki matrisi ne zaman çarpamazsınız?

Tüm matrisler çarpılamaz. İki matrisin çarpılması için ilk matristeki sütun sayısının ikinci matristeki satır sayısına eşit olması gerekir.

Örneğin, birinci matrisin 3 sütunu, ikinci matrisin ise 2 satırı olduğundan aşağıdaki çarpma işlemi yapılamaz:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

Ama sırayı tersine çevirirsek çoğaltılabilirler. Çünkü ilk matrisin iki sütunu, ikinci matrisin ise iki satırı vardır:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

Matris Çarpma Özellikleri

Bu tür matris işlemi aşağıdaki özelliklere sahiptir:

Matris çarpımı ilişkiseldir:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

Matris çarpımı aynı zamanda dağılma özelliğine de sahiptir:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

Matrislerin çarpımı değişmeli değildir:

$\displaystyle A \cdot B \neq B \cdot A$

Örneğin aşağıdaki matris çarpımı bir sonuç verir:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

Ancak matrislerin çarpım sırasını tersine çevirirsek çarpımın sonucu farklıdır:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

Ek olarak herhangi bir matris birim matrisle çarpıldığında aynı matris elde edilir. Buna çarpımsal kimlik özelliği denir:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

Örneğin:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Son olarak, tahmin edebileceğiniz gibi, herhangi bir matrisin sıfır matrisiyle çarpımı sıfır matrisine eşittir. Buna sıfırın çarpımsal özelliği denir:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

Örneğin:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

İki matris nasıl çarpılır?

Çözülmüş matris çarpım alıştırmaları

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

İki matrisi ne zaman çarpamazsınız?

Matris Çarpma Özellikleri

Yorum bırakın Yanıtı iptal et