Rasyonel fonksiyon: nedir, tanım kümesi, asimptotlar, grafik, alıştırmalar,...

Burada rasyonel fonksiyonların ne olduğunu keşfedeceksiniz. Ayrıca rasyonel bir fonksiyonun tanım kümesini ve asimptotlarını nasıl hesaplayacağımızı da açıklıyoruz. Sadece bu da değil, rasyonel fonksiyonların tüm özelliklerinin ne olduğunu göreceksiniz. Son olarak rasyonel fonksiyonlarla ilgili adım adım alıştırmalarla pratik yapabilirsiniz.

Rasyonel fonksiyon nedir?

Rasyonel bir fonksiyonun tanımı aşağıdaki gibidir:

Rasyonel bir fonksiyon, iki polinomun bölümünden oluşan bir fonksiyondur , yani rasyonel bir fonksiyon, payda ve paydada bir polinom içeren bir kesirdir.

Rasyonel fonksiyonlar paydanın sıfırlandığı noktalardaki tekilliklerle karakterize edilir.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Rasyonel fonksiyonlara kesirli fonksiyonlar da denir.

Öte yandan rasyonel fonksiyonları irrasyonel fonksiyonlarla karıştırmamak gerekir. İrrasyonel (veya radikal) fonksiyonlar köklerden oluşan fonksiyonlardır.

Rasyonel Fonksiyon Örnekleri

Rasyonel fonksiyon kavramını daha iyi anlamak için bu tip fonksiyonun birkaç örneğini göreceğiz.

Pay ve paydasında birinci dereceden polinom bulunan rasyonel fonksiyon:

$f(x)=\cfrac{x+3}{2x-5}$

Bu tür rasyonel fonksiyonlara homograf fonksiyonları da denir.

Payında sabit ve paydasında polinom bulunan rasyonel fonksiyon:

$f(x)=\cfrac{7}{x+1}$

Bu tür rasyonel fonksiyonlara ters orantı fonksiyonları denir ve ters orantılı büyüklükleri matematiksel olarak tanımlamak için kullanılır.

Payı üçüncü dereceden polinom ve paydası ikinci dereceden polinom olan rasyonel fonksiyon:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Rasyonel bir fonksiyonun alanı

0’a bölünen bir sayı sonsuzluğu (∞) veren bir belirsizliktir, dolayısıyla payda 0 olmadığı sürece rasyonel bir fonksiyon her zaman mevcut olacaktır.

Bu nedenle rasyonel bir fonksiyonun alanı , paydayı iptal eden değerler dışındaki tüm gerçek sayılardan oluşur.

Dolayısıyla, rasyonel bir fonksiyonun tanım kümesini elde etmek için paydanın 0 olduğu zamanı bulmamız gerekir, çünkü bu nokta tanım kümesine ait olmayan tek nokta olacaktır.

Bir örnek çözerek rasyonel bir fonksiyonun tanım kümesinin nasıl hesaplandığını görelim:

$f(x)=\cfrac{5x}{x+2}$

Önce paydayı 0’a eşitliyoruz, sonra ortaya çıkan denklemi çözüyoruz:

$x+2=0$

$x=-2$

Dolayısıyla x -2 olduğunda payda 0 olacak ve dolayısıyla fonksiyon mevcut olmayacaktır. Dolayısıyla fonksiyonun tanım kümesi x=-2 dışındaki tüm gerçek sayılardan oluşur. Bu şu şekilde ifade edilmektedir:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Rasyonel bir fonksiyonun asimptotları

Rasyonel fonksiyonların temel özelliklerinden biri asimptotlarıdır, çünkü asimptotlar grafiksel temsillerini belirler.

➤ Bakınız: bir fonksiyonun grafik gösterimi

Rasyonel bir fonksiyonun asimptotları, fonksiyonun grafiğinin sonsuza kadar yaklaştığı ancak asla dokunmadığı çizgilerdir.

Üç tür asimptot vardır: dikey asimptotlar, yatay asimptotlar ve eğik asimptotlar.

Aşağıda rasyonel bir fonksiyonun kırmızı grafikle gösterebileceği üç tür asimptot bulunmaktadır.

Rasyonel bir fonksiyonun dikey asimptotu

Rasyonel bir fonksiyonun yatay asimptotu

Rasyonel bir fonksiyonun eğik asimptotu

Gördüğünüz gibi, bir fonksiyonun asimptotunu grafiğinden belirlemek oldukça basittir, ancak rasyonel bir fonksiyonun asimptotlarını grafik gösterimi olmadan hesaplamak oldukça karmaşıktır. Bu nedenle bir fonksiyonun asimptotlarının nasıl hesaplandığını web sitemizde görmenizi öneririz.

Rasyonel bir fonksiyonun özellikleri

Rasyonel fonksiyonlar aşağıdaki özelliklere sahiptir:

$f(x)=\cfrac{P(x)}{Q(x)}$

Yukarıda gördüğümüz gibi rasyonel fonksiyonların tanım kümesi, kesrin paydasını iptal eden değerler dışındaki tüm gerçek sayıları içerir.

Genel olarak rasyonel bir fonksiyonun aralığı (veya aralığı), fonksiyonun yatay asimptotuna sahip olduğu değerler dışındaki tüm gerçek sayıları içerir.

Rasyonel fonksiyonlar kendi alanları boyunca süreklidir. Veya başka bir deyişle rasyonel fonksiyonlar kendi alanlarına ait olmayan noktalarda süreksizlikler gösterirler.

Çoğu rasyonel fonksiyonun grafiksel gösterimi iki hiperbolden oluşur.

Rasyonel fonksiyonların asimptotları için bazı kurallar polinom payından çıkarılabilir.
$P(x)$

ve payda polinomu

$Q(x):$
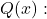
- Rasyonel bir fonksiyonun kökleri olan noktalarda dikey bir asimptotu vardır.
  $Q(x)$
  
  ama bunlar kökleri değil
  
  $P(x).$
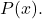
- derecesi ise
  $P(x)$
  
  derecesinden daha azdır
  
  $Q(x)$
  
  y=0 doğrusu rasyonel fonksiyonun yatay bir asimptotudur.
- derecesi ise
  $P(x)$
  
  derecesinden daha büyüktür
  
  $Q(x)$
  
  rasyonel fonksiyonun yatay asimptotu yoktur.
- derecesi ise
  $P(x)$
  
  derecesinden daha büyük bir birimdir.
  
  $Q(x)$
  
  ve iki polinomun ortak bir kökü yoktur, rasyonel fonksiyonun eğik bir asimptotu vardır.

Rasyonel fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki rasyonel fonksiyonun tanım kümesini bulun:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Çözümü görün

Bu rasyonel bir fonksiyondur, yani etki alanı, paydayı iptal edenler dışındaki tüm sayılardan oluşur, çünkü o zaman fonksiyon ∞ verir.

Hangi sayının alana ait olmadığını görmek için tamsayı paydasını sıfıra eşitliyoruz:

$2x+4=0$

Ve ortaya çıkan denklemi çözüyoruz:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Dolayısıyla fonksiyonun tanım kümesi -2 dışındaki sayılardan oluşur:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Alıştırma 2

Aşağıdaki rasyonel fonksiyonun kesme noktalarını Kartezyen eksenlerle bulun:

$f(x)=\cfrac{x^2-9}{x}$

Çözümü görün

X eksenli kesme noktası

Fonksiyonun X ekseni ile kesişme noktasını bulmak için çözmek gerekir

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

İkinci dereceden denklemin iki çözümünü elde ettik, böylece rasyonel fonksiyon apsis eksenini iki farklı noktada keser:

$\bm{(3,0)\qquad (-3,0)}$

Y ekseni ile kesme noktası

Y ekseniyle kesişme noktasını bulmak için hesaplamanız gerekir

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Sıfıra bölünen herhangi bir sayı, sonsuzluğu veren bir belirsizliktir. Dolayısıyla rasyonel fonksiyon Y ekseninin üzerinde hiçbir noktadan geçmez, yani y ekseniyle kesişme noktası yoktur.

Alıştırma 3

Aşağıdaki rasyonel fonksiyonu bir grafik üzerinde çizin:

$y=\cfrac{2x+3}{2x+6}$

Çözümü görün

Yapılacak ilk şey fonksiyonun tanım kümesini hesaplamaktır:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Fonksiyonun tanım kümesini öğrendikten sonra bir değerler tablosu oluştururuz:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Bitirmek için, elde edilen noktaları bir grafikte temsil edin ve hiperbolleri çizin, böylece rasyonel fonksiyonu çizin:

Alıştırma 4

Aşağıda grafiği verilen rasyonel fonksiyonun asimptotlarını belirleyin:

Çözümü görün

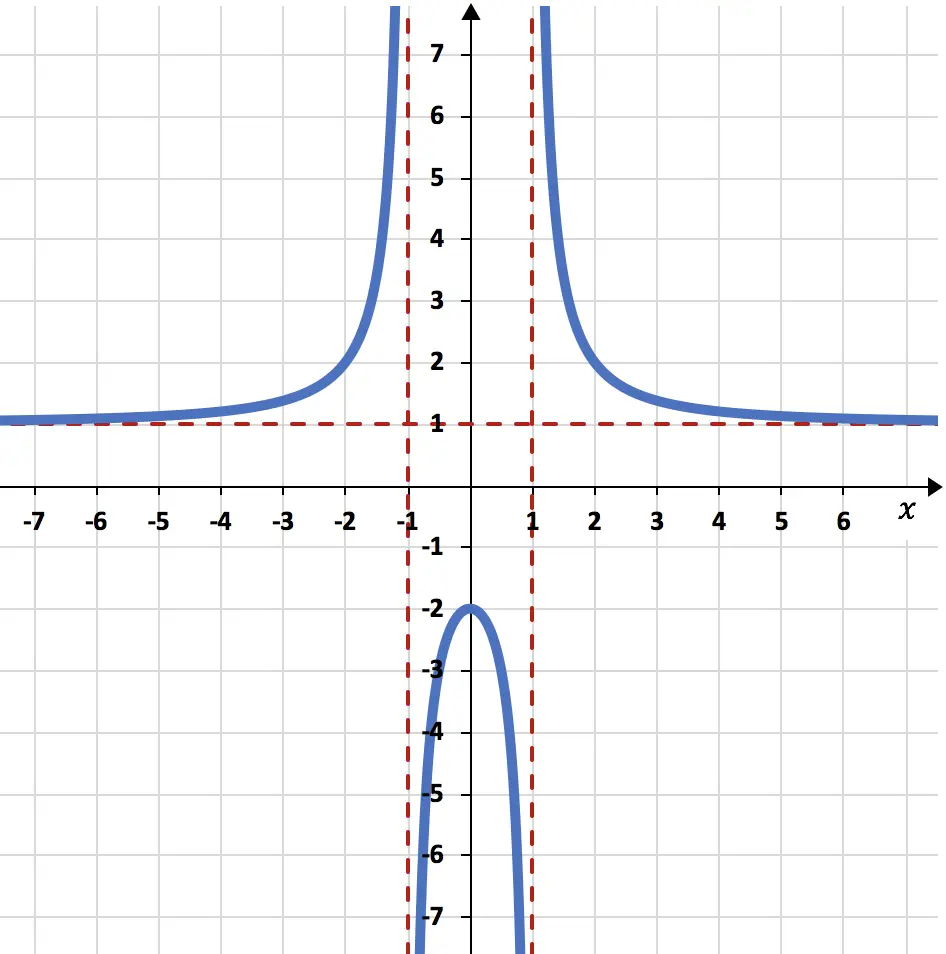
Asimptotlar, kırmızı noktalı çizgilerle temsil edildikleri için grafikte çok net bir şekilde görülebilir.

Bu problemde fonksiyon y=1 yatay çizgisine çok yakındır ancak ona hiç dokunmaz. Bu nedenle rasyonel fonksiyonun tek bir yatay asimptotu vardır; bu da y=1’dir.

Benzer şekilde, fonksiyonun grafiksel gösterimi x=-1 ve x=1 dikey çizgilerine çok yakındır ancak bu değerlere asla ulaşmaz. Dolayısıyla rasyonel fonksiyonun iki farklı dikey asimptotu vardır: x=-1 ve x=1.

Alıştırma 5

Aşağıdaki rasyonel fonksiyonun tüm asimptotlarını hesaplayın:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Not: Bu alıştırmayı çözmek için öncelikle bir fonksiyonun asimptotlarının nasıl hesaplandığını anlatan yukarıdaki bağlantıya gidip açıklamayı görmenizi öneririz.

Çözümü görün

dikey asimptot

Bir fonksiyonun dikey asimptotlarını hesaplamak için önce fonksiyonun tanım kümesini bulmamız gerekir. Bu nedenle, tanım kümesine ait olmayan noktaları bulmak için rasyonel fonksiyonun paydasını 0’a eşitliyoruz:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Dolayısıyla fonksiyonun tanım kümesi -1 dışındaki tüm sayılardan oluşur:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Yani x=-1 dikey bir asimptot olabilir. Bunu kontrol etmek için fonksiyonun limitini şu noktada hesaplamamız gerekir:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Dolayısıyla x=-1 rasyonel fonksiyonun dikey bir asimptotudur çünkü fonksiyonun bu noktadaki limiti sonsuzluğu verir.

Yatay asimptot

Yatay asimptotları belirlemek için fonksiyonun sonsuz limitini hesaplamamız gerekir:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

Bu durumda sonsuzluk arasındaki belirsiz sonsuz sınırın sonucu, pay ve payda aynı mertebeden olduğundan en yüksek derecedeki x’in katsayılarının bölümüdür.

Fonksiyonun iki sonsuz limiti bize 3 değerini verdi, dolayısıyla y=3 rasyonel fonksiyonun yatay bir asimptotudur.

eğik asimptot

Yatay bir asimptot olduğundan rasyonel fonksiyonun eğik bir asimptotu yoktur.