Burada benzer tek terimlilerin ne olduğuna dair açıklama bulacaksınız. Ek olarak, benzer tek terimlilerin örneklerini görebilecek ve hatta bu tür tek terimlilerin çözülmüş alıştırmalarıyla pratik yapabileceksiniz.
Benzer monomlar nelerdir?
Açıkçası, benzer tek terimlilerin anlamını anlamak için öncelikle bir tek terimlinin ne olduğunu bilmeniz gerekir. Bu yüzden devam etmeden önce bağlantılı sayfaya göz atmanızı öneririm.
Dolayısıyla, iki monomiyalin benzer olması şu anlama gelir:
Benzer monomlar, tam olarak aynı değişmez kısma sahip olan monomlardır. Başka bir deyişle, iki veya daha fazla tek terimli sayılar aynı değişkenlerden (harflerden) ve aynı üslerden oluştuklarında benzerdir.
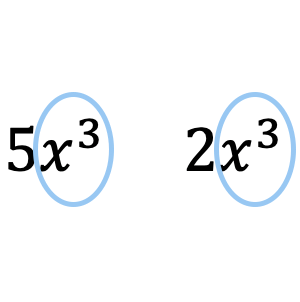
Yukarıdaki örnekte görebileceğiniz gibi, tek terimli
![]()
tek terimliye benzer
![]()
çünkü ikisi de aynı gerçek kısma sahip
![]()
Katsayıları farklı olsa bile.
Benzer tek terimlilerin özelliklerinden biri de, evet veya evet konusunda ustalaşmanız gereken iki işlem olan hem tek terimlileri toplamak hem de çıkarmak için kullanılmalarıdır. Tek terimlilerin nasıl ekleneceğini veya çıkarılacağını görmek için iki bağlantıdan birine tıklayın. Ayrıca her bağlantıda adım adım çözülmüş örnekler ve alıştırmalar bulacaksınız.
Aslında, tek terimlileri yalnızca benzer olmaları durumunda toplayıp çıkarabilirsiniz. Benzer tek terimlilerin matematikte bu kadar önemli olmasının nedeni tam olarak budur.
Benzer monomların örnekleri
Benzer tek terimli kavramını tam olarak anlayabilmeniz için aşağıda birbirine benzer birkaç tek terimli örnek görebilirsiniz.
örnek 1
![]()
Önceki 2 monom, gerçek kısımları eşdeğer olduğundan benzerdir
![]()
Örnek 2
![]()
Önceki üç tek terimlilerin gerçek kısımları aynı olduğundan benzerdir
![]()
Örnek 3
![]()
![]()
Önceki dört monom, gerçek kısımları aynı olduğundan birbirine benzer
![]()
Benzer tek terimlilerin çözülmüş alıştırması
Benzer görünen tek terimli çiftleri eşleştirin:
![Rendered by QuickLaTeX.com \begin{array}{lcl} 4x^2 & \qquad \qquad & 2a^5x^6z \\[3ex]-3a^5x^6z & \qquad \qquad & 6x^2y^3z^6w^2 \\[3ex] 9y^3x & \qquad \qquad & 2xy^3 \\[3ex]4x^2y^3z^6w^2& \qquad \qquad & x^2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ca52625823eec990ff41ecd05d5c1149_l3.png)
Benzer monomlar, aynı değişmez parçalara sahip olanlardır. Bu nedenle, benzer tek terimlilerin çiftleri şunlardır:
![]()
![]()
![]()
![]()
Her ne kadar tamamen farklı bir anlama gelse de, buraya kadar geldiyseniz muhtemelen bir sayının polinom ayrışımının ne olduğunu bilmekle de ilgileniyorsunuzdur. Çünkü bu çok az kişinin bildiği bir konu ama aslında matematiksel ifadeleri basitleştirmek açısından oldukça faydalı.