Bir doğrunun ve bir düzlemin göreli konumları

Bu sayfada bir doğrunun ve bir düzlemin göreceli konumlarını bulacaksınız. Bir doğru ile bir düzlem arasındaki göreceli konumun nasıl hesaplandığını size açıklıyoruz (2 yöntem) ve ayrıca adım adım çözülmüş örnekleri ve alıştırmaları görebileceksiniz.

Bir doğru ile bir düzlem arasındaki göreceli konumlar nelerdir?

Bir doğru ile bir düzlem arasındaki olası tüm göreceli konumlara bakmadan önce, elbette doğruların ve düzlemin ne olduğunu bilmemiz gerekir. Dolayısıyla eğer bu iki kavramı hala çok net anlayamadıysanız öncelikle detaylı bir şekilde anlatıldığı bağlantılı sayfalara göz atmanızı öneririz.

Dolayısıyla analitik geometride uzayda bir çizgi ile bir düzlem arasında yalnızca üç göreceli konum vardır:

Düzlemde bulunan doğru : Doğru düzlemde yer aldığında bu, sonsuz sayıda ortak noktaya sahip oldukları anlamına gelir.
Paralel Doğru ve Düzlem : Ortak noktaları olmayan bir doğru ve düzlem paraleldir.
Kesişen doğru ve düzlem : Bir doğru ve bir düzlem, doğru düzlemi bir noktada kestiğinde kesişir. Yani tek bir ortak noktaları var.

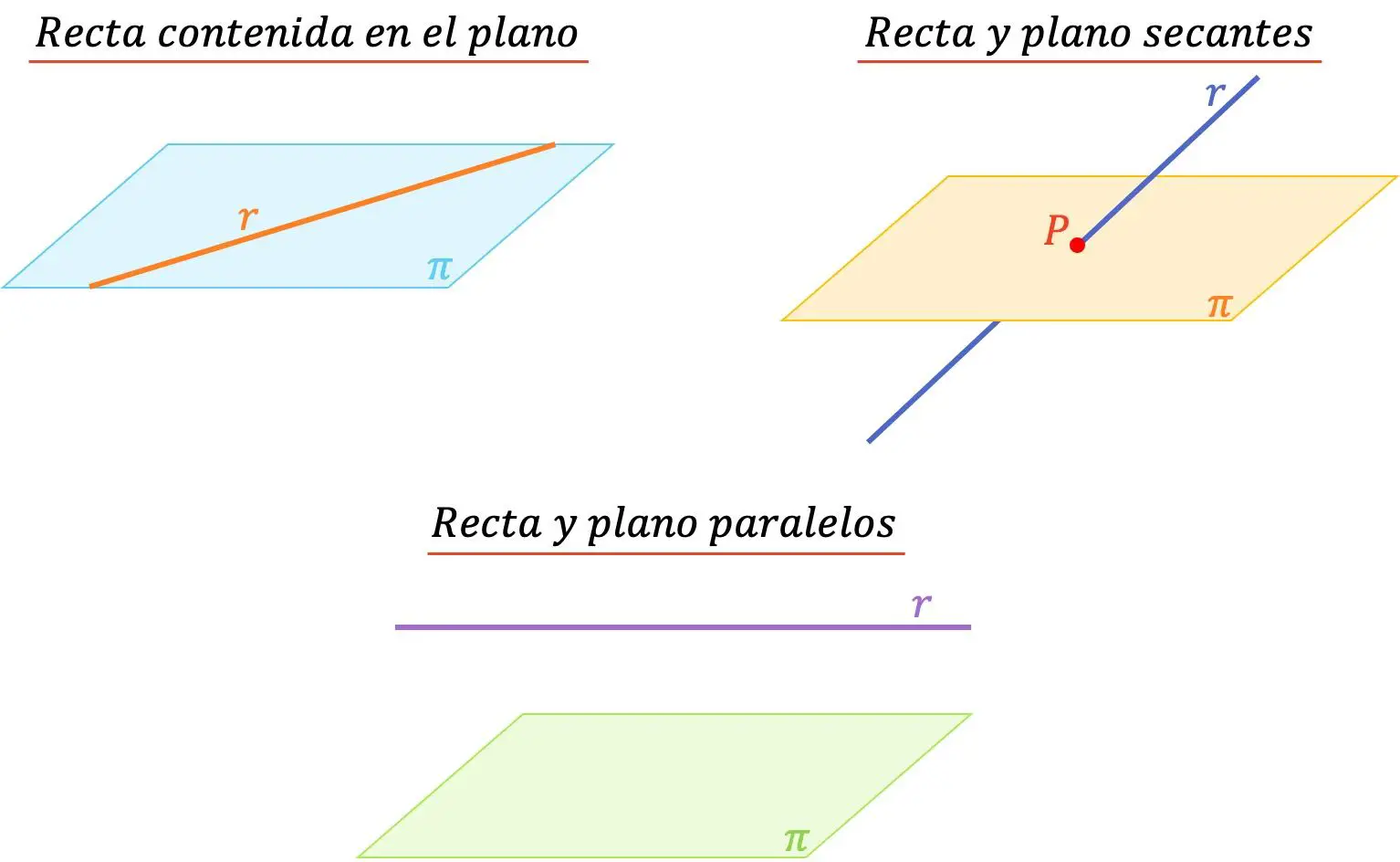
Öte yandan doğru düzlemin içinde kaldığında veya birbirlerine paralel olduklarında oluşturdukları açı 0° olacaktır. Öte yandan, doğru ve düzlem kesiştiğinde iki geometrik eleman arasındaki açı 0° (dahil değil) ila 90° (dahil) arasında değişebilir.

Bir doğrunun ve bir düzlemin göreceli konumu nasıl hesaplanır?

Uzayda bir çizgi ile bir düzlem arasındaki göreceli konumu bulmak için esas olarak iki yöntem vardır: aralıklara göre veya vektörlere göre .

Doğru örtülü (veya genel) bir denklem olarak ifade edildiğinde sıralama yöntemini kullanmak daha kolaydır. Öte yandan doğru başka bir denklem türüyle verilmişse, örneğin vektör, parametrik veya sürekli denklem biçimindeyse vektör yöntemini kullanmak daha hızlıdır.

Doğrunun denklemlerinin nasıl göründüğünü hatırlamıyorsanız, size doğrunun tüm denklemlerine başvurabileceğiniz bir sayfa bırakıyoruz. Burada doğrunun tüm denklemlerini, iki noktadan geçen bir doğrunun denklemini hızlı bir şekilde bulmanızı sağlayacak bir formülü, örnekleri ve adım adım çözülmüş alıştırmaları bulacaksınız.

Bu nedenle soruna göre şu veya bu yöntemi kullanmak daha pratiktir, bu nedenle her iki işlemin de nasıl yapılacağını bilmenizi öneririz. Aşağıda her iki yöntemin örneklerle açıklaması bulunmaktadır.

Çizgi örtülü (veya genel) bir denklem biçiminde olduğunda

Bir doğru ile bir düzlem arasındaki göreceli konumu belirlemenin bir yolu, iki matrisin sıralamasını hesaplamaktır.

Doğru, örtülü (veya genel) denklemleriyle tanımlanmışsa:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

Plan ayrıca genel bir denklem biçiminde de ifade edilir:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Düzlem ve doğru denklemlerinin A, B ve C katsayılarından oluşan matrise A adını vereceğiz:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

Ve A’ matrisi, iki denklemin tüm katsayılarını içeren genişletilmiş matris olacaktır:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Daha sonra çizgi ile düzlem arasındaki göreceli konum, aşağıdaki tabloya göre önceki iki matrisin kapsamının değerine göre belirlenir:

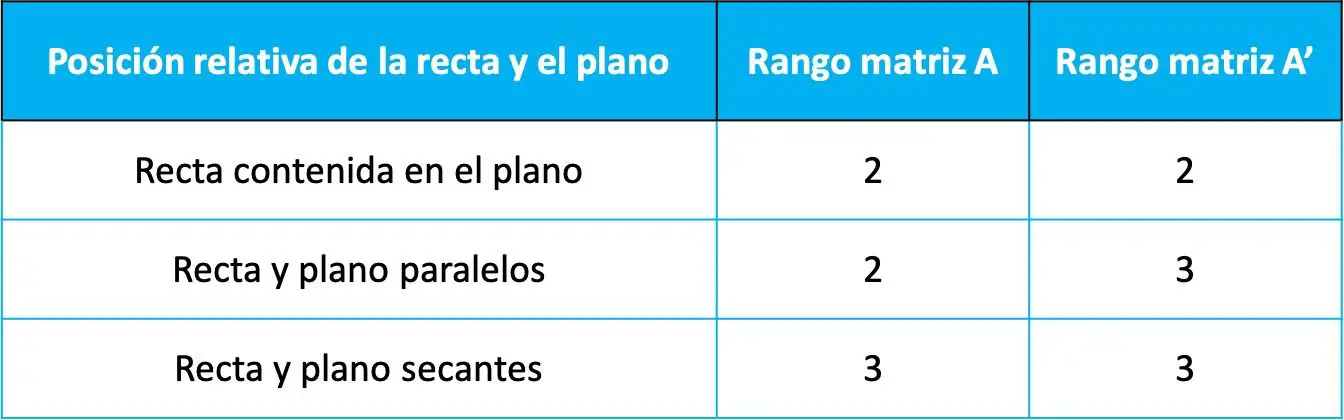
uzayda bir çizgi ile bir düzlem arasındaki göreceli konumu aralıklara göre inceleyin

Göreceli konumların bu iki matrisin mertebelerine bağlı olduğu Rouche-Frobenius toereminden (doğrusal denklem sistemlerini çözmek için kullanılan bir teorem) gösterilebilir. Ancak bu sayfada gösteriyi yapmayacağız çünkü bunu bilmek gerekli değildir ve bu da pek bir şey sağlamaz.

Bir çizginin ve bir düzlemin göreli konumunun aralıklara göre nasıl bulunacağına ilişkin örnek

Bunun nasıl yapıldığını tam olarak görebilmeniz için örnek olarak bir alıştırma çözeceğiz:

Aşağıdaki çizgi ile aşağıdaki düzlem arasındaki göreceli konumu inceleyin:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

Doğru, kesişen iki düzlemle tanımlanır, yani örtülü bir denklem olarak ifade edilir. Bu nedenle çizgi ile düzlem arasındaki göreceli konumu incelemek için sıra yöntemini kullanacağız.

Yapılacak ilk şey, A matrisini ve genişletilmiş A’ matrisini denklemlerin katsayılarıyla oluşturmaktır:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

Şimdi her matrisin rütbesini hesaplamamız gerekiyor. İlk önce A matrisinin kapsamını determinantlarla buluyoruz:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

A matrisinin determinantı sıfırdır ancak determinantı sıfırdan farklı olan 2×2’lik bir alt matris içerir, dolayısıyla bu matris 2. sıralı bir matristir.

Öte yandan A’ matrisinin rütbesinin de hesaplanması gerekir. Ve genişletilmiş A’ matrisinin aralığı her zaman en azından A matrisinin aralığıyla aynı olacaktır, bu nedenle bunun 3. veya 2. sırada olup olmadığını kontrol etmemiz yeterlidir:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

Öte yandan, genişletilmiş A’ matrisinin 0’dan farklı bir 3×3 alt determinantı vardır, bu nedenle rütbesi 3’tür.

Yani A matrisi rütbe 2 ve A’ matrisi rütbe 3 olduğundan, doğru ve düzlem paraleldir .

Çizgi başka bir denklem türü biçiminde olduğunda

Doğru, ister vektör, ister parametrik veya sürekli denklem olsun, örtülü denklem dışında bir denklemle ifade edildiğinde aşağıda açıkladığımız yöntemin kullanılması tercih edilir.

Yani doğru bir vektör denklemi, parametrik denklem veya sürekli bir denklem şeklinde verilmişse bu, doğruya ait bir noktayı ve onun yön vektörünü bildiğimiz anlamına gelir.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

Öte yandan, düzleme normal (veya dik) vektörün ne olduğunu da biliyoruz:

$\vv{n} \perp \pi$

Daha sonra, 2 vektörden ve doğrunun noktasından, doğru ile düzlem arasındaki göreceli konum şu şekilde hesaplanabilir:

Doğrunun yön vektörü ile düzleme dik vektör arasındaki skaler çarpım sıfırdan farklıysa bu, doğrunun düzleme kesen olduğu anlamına gelir.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
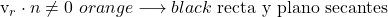
Ancak doğrunun yön vektörü ile düzleme dik vektör arasındaki skaler çarpım sıfıra eşitse, iki olasılık vardır: doğru düzlemin içindedir veya paraleldir. Hangi durumun olduğunu bilmek için doğru üzerindeki bir noktanın koordinatlarını düzlem denkleminde yerine koymamız gerekir.
- Nokta düzlem denklemini sağlıyorsa doğru düzlemin içinde kalır.
- Öte yandan nokta düzlem denklemini sağlamıyorsa doğru ve düzlem paraleldir.

Vektörleri kullanarak bir doğrunun ve bir düzlemin göreceli konumunu belirleme örneği

Bu yöntemin teorisini gördükten sonra şimdi adım adım çözülen bir alıştırmaya bakalım:

Aşağıdaki çizgi ile aşağıdaki düzlem arasındaki göreceli konumu bulun:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Birincisi, çizgi parametrik denklemler olarak tanımlanır, dolayısıyla yön vektörü ve içinden geçtiği nokta şöyledir:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

Ve diğer taraftan düzleme normal olan vektör:

$\vv{n} =(2,1,-2)$

Doğrunun yön vektörünü ve düzleme dik vektörü bildiğimizde, ikisi arasındaki skaler çarpımı hesaplamamız gerekir:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Nokta çarpımın sonucu sıfırdır, dolayısıyla çizgi yalnızca düzlemin içinde yer alabilir veya ona paralel olabilir. Hangi durumun olduğunu bulmak için doğru üzerindeki noktanın Kartezyen koordinatlarını düzlem denkleminde yerine koyarız:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Doğrunun noktasını düzlem denkleminde değiştirerek bir eşitlik elde ederiz, dolayısıyla nokta düzlemin denklemine uyar ve sonuç olarak doğru düzlemin içinde kalır .

Bir doğrunun ve bir düzlemin göreceli konumları