Bir doğru ile bir düzlem arasındaki açı

Burada bir doğru ile düzlem arasındaki açının nasıl hesaplandığını bulacaksınız. Ayrıca örnekleri görebilecek ve ayrıca doğrular ve düzlemler arasındaki açılarla ilgili adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Bir doğru ile bir düzlem arasındaki açı nedir?

Bir çizgi ile bir düzlem arasındaki açı, çizgi ile onun düzlem üzerindeki dik izdüşümü arasındaki açıdır.

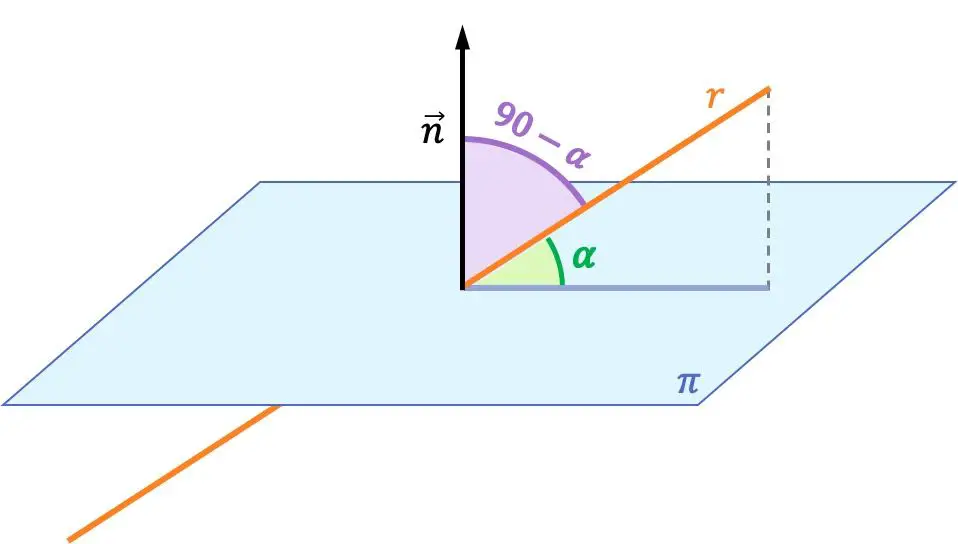
Bir doğru ile bir düzlem arasındaki açı, söz konusu doğru ile düzleme dik vektör arasındaki açının tamamlayıcısıdır. Bu nedenle bir doğru ile bir düzlem arasındaki açı, doğrunun yön vektörü ile düzlemin normal vektörü arasındaki açıdan hesaplanır.

Bir doğru ile bir düzlem arasındaki açı formülü

Bir düzlem ile bir doğru arasındaki açının formülünü bulmak için iki vektör arasındaki açının nasıl bulunacağını bilmeniz gerekir. Bağlantılı sayfada açıklamanın yanı sıra adım adım çözülmüş örnekler ve alıştırmalar bulacaksınız, bu yüzden nasıl yapacağınızı hatırlamıyorsanız bir göz atmanızı öneririz.

Böylece bir doğru ile bir düzlem arasındaki açı, söz konusu doğrunun yön vektörü arasındaki açının tamamlayıcısı olduğundan

$(\vv{\text{v}}_r)$

ve söz konusu düzlemin normal vektörü

$(\vv{n})$

İki vektör arasındaki açı formülünden, bir doğru ile bir düzlem arasındaki açının aşağıdaki ifadeye eşdeğer olduğu sonucunu çıkarıyoruz:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Bu nedenle bir doğru ile bir düzlem arasındaki açının formülü şu şekildedir :

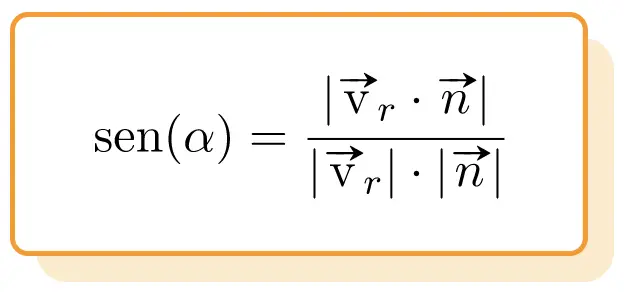
bir çizgi ile formül düzlemi arasındaki açı

Altın:

$\vv{\text{v}}_r$

doğrunun direkt vektörüdür.
$\vv{n}$

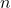
düzleme normal vektördür.

Bir çizgi ile düzlem arasındaki açıyı hesaplama örneği

Bu tür bir problemi nasıl çözeceğinizi görebilmeniz için burada bir doğru ile düzlem arasındaki açının hesaplanmasına ilişkin bir örnek verilmiştir:

Doğrunun oluşturduğu açıyı hesaplayın
$r$

uçakla

$\pi.$

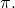
Denklemleri şöyle olsun:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

Doğru, parametrik denklemler biçiminde ifade edilir, dolayısıyla yön vektörü şöyledir:

$\vv{\text{v}}_r = (-1,4,-3)$

Öte yandan, düzlem örtülü (veya genel) bir denklem biçiminde tanımlanır, dolayısıyla normal vektörü şöyledir:

$\vv{n} = (1,-1,4)$

Böylece, doğrunun yön vektörünü ve düzlemin normal vektörünü bildiğimizde, doğru ile düzlem arasındaki açı formülünü uygularız:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Vektörleri formülde değiştiririz:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

Ve hesaplamaları yapıyoruz:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Son olarak hesap makinesiyle sinüsü ters çevirip açının değerini buluyoruz:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

Bu nedenle çizgi ile düzlem arasındaki açı yaklaşık 51,80°’dir.

Eğer 0° sonucunu elde edersek bu, doğru ile düzlemin paralel olduğu veya doğrunun düzlemin içinde kaldığı anlamına geldiğini dikkate almalıyız. Ve eğer açı 90 dereceye eşitse bu, doğrunun ve düzlemin birbirine dik olduğu anlamına gelir.

Bir doğru ile bir düzlem arasındaki açıyla ilgili çözülmüş problemler

1. Egzersiz

Doğrunun oluşturduğu açıyı bulun

$r$

uçakla

$\pi.$

Denklemleri şöyle olsun:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

Çözüme bakın

Çizgi sürekli bir denklem olarak ifade edilir, dolayısıyla yön vektörü şöyledir:

$\vv{\text{v}}_r = (2,-1,-3)$

Öte yandan, düzlem örtülü (veya genel) bir denklem biçiminde olduğundan normal vektörü şöyledir:

$\vv{n} = (3,1,2)$

Böylece, doğrunun yön vektörünü ve düzlemin normal vektörünü bildiğimizde, bir doğru ile bir düzlem arasındaki açı formülünü kullanırız:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Son olarak sinüsü ters çevirip açının değerini buluyoruz:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Bu nedenle doğru ile düzlem arasındaki açı 4,10°’dir.

Alıştırma 2

Çizginin oluşturduğu açıyı belirleyin

$r$

uçakla

$\pi.$

Denklemleri şöyle olsun:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

Çözüme bakın

Çizgi örtülü (veya genel) denklemleriyle ifade edilir, bu nedenle çizgiyi belirleyen 2 düzleme normal vektörlerin vektör çarpımını hesaplayarak çizginin yön vektörünü bulmak gerekir:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

Öte yandan, düzleme normal olan vektör:

$\vv{n} = (-4,2,0)$

Böylece, doğrunun yön vektörünü ve düzlemin normal vektörünü bildiğimizde, bir doğru ile bir düzlem arasındaki açı formülünü kullanırız:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Son olarak sinüsü ters çevirip açının değerini buluyoruz:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Dolayısıyla doğru ile düzlem arasındaki açı 46,33°’dir.

Alıştırma 3

Bir doğru ile bir düzlem arasındaki açı formülünü kullanarak, değerini bulun.

$k$

hak için gerekli

$r$

ve uçak

$\pi$

paralel olun.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

Çözüme bakın

İlk olarak, doğru bir vektör denklemi olarak ifade edilir, dolayısıyla yön vektörü şöyledir:

$\vv{\text{v}}_r = (4,-1,3)$

Öte yandan düzlem genel bir denklem biçiminde olduğundan normal vektörü şöyledir:

$\vv{n} = (4,3,k)$

Yani iki geometrik elemanın paralel olması için aralarındaki açının sıfır olması gerekir. Bu nedenle bir doğru ile bir düzlem arasındaki açının formülü şöyledir:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Bu nedenle doğrunun yön vektörü ile normal vektör arasındaki nokta çarpımı sıfır olmalıdır. Ve bu denklemden bilinmeyenin değerini belirleyebiliriz

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Son olarak, bu makaleyi yararlı bulduysanız, muhtemelen iki düzlem arasındaki açının nasıl bulunacağıyla da ilgileniyorsunuzdur. Bağlantılar sayfasında iki farklı düzlem arasındaki açıyı hesaplamak için gerekli formülün yanı sıra çok ayrıntılı bir açıklama bulacaksınız ve ayrıca pratik yapabilmek ve anlayabilmek için adım adım çözülmüş örnekleri ve alıştırmaları görebileceksiniz. nasıl mükemmel bir şekilde yapıldığını.

Bir doğru ile bir düzlem arasındaki açı nedir?

Bir doğru ile bir düzlem arasındaki açı formülü

Bir çizgi ile düzlem arasındaki açıyı hesaplama örneği

Bir doğru ile bir düzlem arasındaki açıyla ilgili çözülmüş problemler

1. Egzersiz

Alıştırma 2

Alıştırma 3

Yorum bırakın Yanıtı iptal et