Vektörler (matematik) nedir? -Mathority

Bu sayfada vektörler hakkında her şeyi bulacaksınız: Ne oldukları, özellikleri, nasıl hesaplandıkları, vektörlerle işlemlerin nasıl yapılacağı, var olan farklı türleri,…

Vektör nedir?

Bir vektörün matematiksel tanımı aşağıdaki gibidir:

Matematikte bir vektör, bir noktadan (başlangıç olarak adlandırılır) başka bir noktaya (son olarak adlandırılır) giden yönlendirilmiş bir parçadır.

Örneğin aşağıdaki grafikte vektörün olduğunu görebilirsiniz.

$\vv{AB}$

Başlangıç noktası A noktası ve bitiş noktası B noktasıdır.

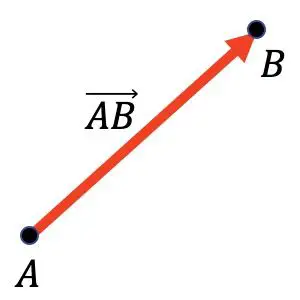
Vektörler çoğunlukla matematikte, özellikle geometri ve fizikte vektör kuvvetlerini grafiksel olarak temsil etmek için kullanılır.

Bir vektörün özellikleri

Vektörlerin matematiksel anlamının ne olduğunu gördükten sonra şimdi de özelliklerinin neler olduğuna bakalım.

Her vektör aşağıdaki geometrik özelliklere sahiptir:

Yön : Bir vektörün yönü, vektörü içeren doğrunun veya ona paralel herhangi bir doğrunun yönüdür. Başka bir deyişle, bir vektörün yönü, üzerinde bulunduğu doğrudur.
Yön : Bir vektörün yönü, söz konusu vektörün okla gösterilen yönüdür.
Modül (veya büyüklük): Bir vektörün modülü uzunluğudur ve vektörün sayısal değerine karşılık gelir. Dolayısıyla vektörün anlamı ne kadar büyükse temsil ettiği vektör miktarı da o kadar büyüktür.
Uygulama noktası : Bir vektörün uygulama noktası, söz konusu vektörün orijinidir.

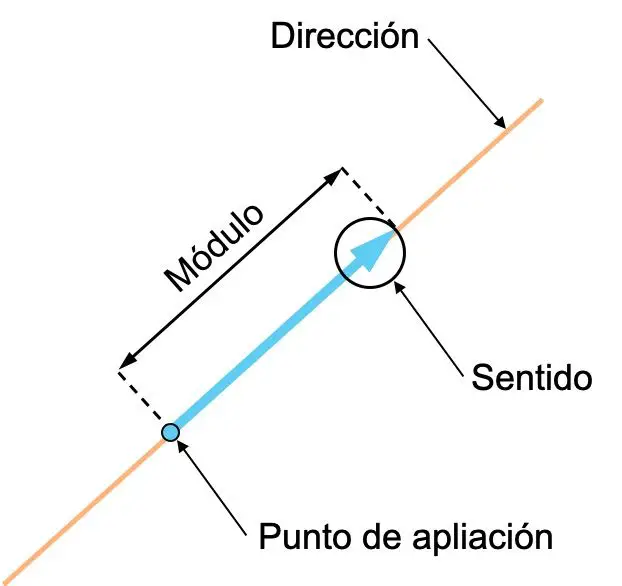
Bir vektörün yönü ve yönü kavramları çoğu zaman kafa karıştırıcıdır, dolayısıyla aralarındaki farkı ayırt etmek önemlidir. İki vektör içeren aşağıdaki örneğe bakın; her ikisi de aynı yöne sahiptir ancak anlamları farklıdır:

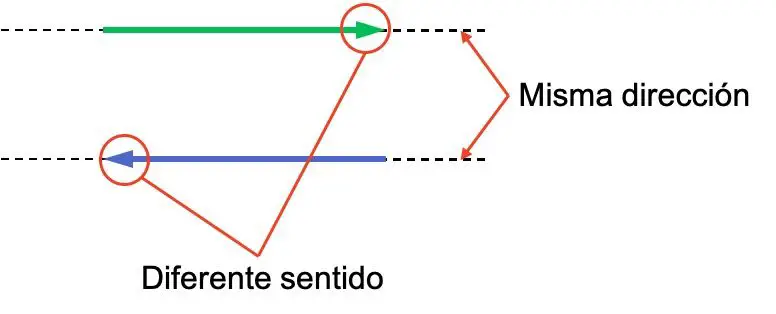
İki vektör paralel olduğundan aynı yöne sahiptir. Bunun yerine, geriye doğru baktıklarından yönleri zıttır.

Bir vektörün bileşenleri

Vektörlerin grafiksel olarak oklarla temsil edildiğini az önce gördük, ancak vektörler aynı zamanda bir vektörün bileşenleri (veya koordinatları) ile sayısal olarak da temsil edilebilir.

Örneğin, bir grafikte aşağıdaki vektör temsil ediliyorsa:

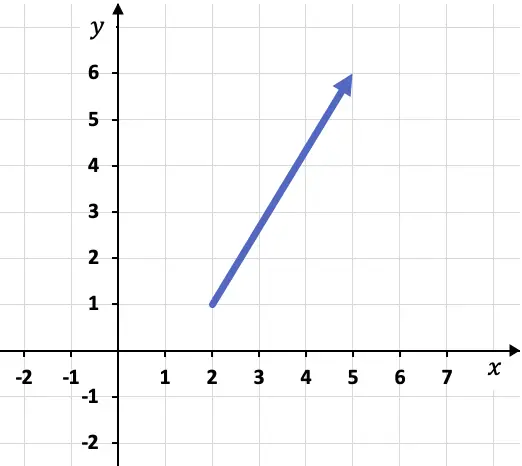
Vektörün bileşenlerini hesaplamak için öncelikle başlangıç ve bitiş koordinatlarını yani başladığı ve bittiği noktaları belirlememiz gerekir. Bu durumda vektörün orijini ve sonu şöyledir:

Vektörün kökeni: A(2,1)

Vektörün bitiş noktası: B(5,6)

Yani, vektörün koordinatlarını veya bileşenlerini bulmak için bitiş noktasından başlangıç noktasını çıkarmanız yeterlidir:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Böylece grafikte temsil edilen vektörün bileşenleri şöyledir:

$\vv{\bm{AB}}\bm{=(3,5)}$

Vektör işlemleri

vektör ekleme

İki vektörü sayısal olarak toplamak için ilgili bileşenlerini eklemelisiniz. Veya başka bir deyişle iki vektörün X koordinatları toplanır ve Y koordinatlarıyla aynıdır.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Bunun nasıl yapıldığını görebilmeniz için aşağıdaki iki vektörü ekleyeceğiz:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Grafiksel gösterimlerinden iki vektör de eklenebilir. Bunun için normalde paralelkenar kuralı veya kanunu kullanılır, ancak birçok yöntem vardır. Burada iki vektörün grafiksel olarak nasıl ekleneceğine ilişkin örnekleri ve çözülmüş alıştırmaları görebilirsiniz.

vektör çıkarma

İki vektörü analitik olarak çıkarmak için ilgili bileşenlerini çıkarmalısınız. Yani iki vektörün X koordinatları birbirinden çıkarılır ve Y koordinatlarıyla aynıdır.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

Örnek olarak aşağıdaki iki vektörü çıkaracağız:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Toplama gibi, 2 vektörü de gösterimlerini kullanarak çıkarabilirsiniz. Bunun için genellikle üçgen kuralı veya kanunu kullanılır ancak birkaç yöntem de vardır. Bunların hepsini örneklerle ve iki vektörün grafiksel olarak nasıl çıkarılacağına dair çözümlü alıştırmalarla görebilirsiniz.

bir vektörün modülü

Bu sayfanın başında gördüğümüz gibi, bir vektörün büyüklüğü o vektörün uzunluğuna karşılık gelir. Bir vektörün uzunluğu (veya büyüklüğü) bileşenlerinden belirlenebilir.

Herhangi bir vektörü düşünün:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Düzlemdeki bir vektörün büyüklüğünü bulmak için aşağıdaki formülü uygulamamız gerekir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

Örneğin aşağıdaki vektörün büyüklüğünü aşağıdaki formülü kullanarak hesaplayacağız:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Çok basit gibi görünse de bir vektörün büyüklüğünü belirlemek karmaşık olabilir. Daha fazla örnek görmek ve bir vektör modülüne ilişkin çözülmüş alıştırmalar yapmak istiyorsanız bu bağlantılı sayfayı ziyaret etmenizi öneririz.

Bir vektörün bir skalerle çarpımı

Bir vektörün çarpımını bir sayıyla (veya bir skalerle) sayısal olarak hesaplamak için, vektörün her bir bileşeninin bu sayıyla çarpılması gerekir.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

Aşağıdaki genel örnekte, skalerin işaretine bakılmaksızın vektörün yönünün nasıl korunduğunu görebilirsiniz. Öte yandan vektörün yönü çarptığı sayının işaretine bağlıdır.

bir sayının veya skalerin bir vektörle çarpımı veya çarpımı

Aşağıda bir vektör ile bir sayının çarpımının nasıl bulunacağına ilişkin sayısal bir örnek görebilirsiniz:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Skaler çarpım

Analitik geometride nokta çarpım, iki vektörü çarparak bunları gerçek sayıya dönüştüren bir vektör işlemidir.

Dolayısıyla iki vektörün nokta çarpımının formülü aşağıdaki gibidir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Aşağıda iki vektör arasındaki nokta çarpımın sonucunun hesaplandığı bir örnek verilmiştir:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

Bu bağlantıda nokta çarpımın daha fazla örneğini görebilirsiniz. Ek olarak, iki vektör arasındaki nokta çarpımı bulmanın başka bir yolunu, vektörlerle bu tür işlemlerin özelliklerini ve adım adım çözülen alıştırmaları bulacaksınız.

vektör çarpımı

İsim olarak çok benzer olmalarına rağmen nokta çarpım ve çapraz çarpım tamamen farklıdır.

Çapraz çarpım , aynı zamanda çapraz çarpım olarak da adlandırılır, uzaydaki (R3’teki) iki vektör arasındaki bir işlemdir, yani bunlar üç koordinatlı vektörlerdir.

Yani, herhangi iki üç boyutlu vektörümüz varsa:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

İki vektörün çapraz çarpımı aşağıdaki 3×3 determinantın sonucuna eşittir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

vektörler nerede

$\vv{i}, \vv{j},\vv{k}$

sırasıyla X, Y, Z eksenleri yönündeki birim vektörlerdir.

Ek olarak, elde edilen vektörün yönü çarpılan iki vektöre diktir.

Tahmin edebileceğiniz gibi, bu tür işlemleri çözmek öncekilere göre daha zordur ve bu nedenle, iki vektör arasındaki çapraz çarpımın nasıl hesaplandığıyla ilgili ayrıntılı bir açıklama içeren bir sayfamız var. Bu nedenle eğer ilgileniyorsanız ziyaret etmenizi ve çözülmüş vektör çarpımı alıştırmalarıyla pratik yapmanızı öneririz.

karışık ürün

Üç vektörün karışık çarpımı , aynı zamanda üçlü nokta çarpımı olarak da adlandırılır, iki farklı işlem türünü içeren üç vektörün ardışık çarpımıdır: nokta çarpım ve vektör çarpımı. Yani, iki vektör işleminin birleşimi bir skaler (gerçek sayı) verir.

Somut olarak, karma çarpım, iki vektörün vektör çarpımının hesaplanmasından ve ardından elde edilen sonucun üçüncü bir vektörle vektörel olarak çarpılmasından oluşur. Formüle bakın:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Vektör çarpımında olduğu gibi vektörler arasındaki karışık çarpımı çözmek de kolay değildir. Bu nedenle örnekler, çözülmüş alıştırmalar ve bu vektör işleminin geometrik anlamını bulabileceğiniz bu üç vektörün karma çarpımı açıklamasına göz atmanızı öneririz.

vektör türleri

Birçok farklı vektör türü vardır ancak bilinmesi gereken en önemli tanımlar şunlardır:

Birim vektör : Modülü 1’e eşit olan vektör.
Sabit vektör : Vektörün orijini sabit bir noktaya uygulandığında vektör sabittir.
Serbest vektör : Bir vektör, uygulama noktası tanımlanmadığında serbesttir ancak serbest bir noktadır.
Eşdoğrusal vektörler : İki veya daha fazla vektör aynı etki çizgisini (vektörün bulunduğu çizgi) paylaşıyorsa eşdoğrusaldır.
Eşdeğer vektörler : İki vektör aynı boyuta, aynı anlama ve aynı yöne sahipse (farklı uygulama noktalarına sahip olabilseler de) eş polendir.
Bağlantılı Vektörler : Bağlantılı vektörler aynı çizgi üzerinde etki eden eşpolen vektörlerdir.
Zıt vektörler : Aynı büyüklükte ve aynı yönde ancak farklı yönlerde olan iki vektör zıttır.
Konum vektörü : konum vektörü, kökeni (0,0) noktası (koordinatların başlangıcı) olan vektördür.
Rekabet eden vektörler : iki veya daha fazla vektör, etki çizgileri aynı noktadan geçtiğinde, yani kesiştiklerinde eşzamanlıdır.
Paralel vektörler : İki veya daha fazla vektör, yönleri ne olursa olsun aynı yöne sahiplerse paraleldir.
Dik vektörler : Yönleri 90°’lik bir açı oluşturduğunda iki vektör diktir (veya diktir).
Ortonormal vektörler : İki veya daha fazla vektör birbirlerine dik ise ortonormaldir ve ayrıca üniterdirler (büyüklükleri birliğe eşittir).
Eş düzlemli vektörler : İki veya daha fazla vektör aynı düzlemde yer aldığında eş düzlemlidir.

İki vektör arasındaki açı

Verilen iki vektör arasındaki açıyı bulmak için aşağıdaki formülü uygulamalıyız:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Altın

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

vektörlerin modülleri

$\vv{\text{u}}$

$\vv{\text{v}}$

sırasıyla.