Bu sayfada düzlemin ne olduğu, nasıl hesaplandığı ve tüm özelliklerinin açıklamasını bulacaksınız. Ek olarak düzlem örneklerini, iki düzlem arasındaki göreceli konumların neler olduğunu, 2 düzlem arasındaki açının nasıl belirleneceğini ve son olarak herhangi bir düzlemin düzlem denklemlerini kullanarak sayısal olarak nasıl ifade edileceğini görebileceksiniz.
Plan nedir?
Analitik geometride düzlemin tanımı şu şekildedir:
Düzlem, iki boyutu (uzunluk ve genişlik) olan geometrik bir nesnedir.
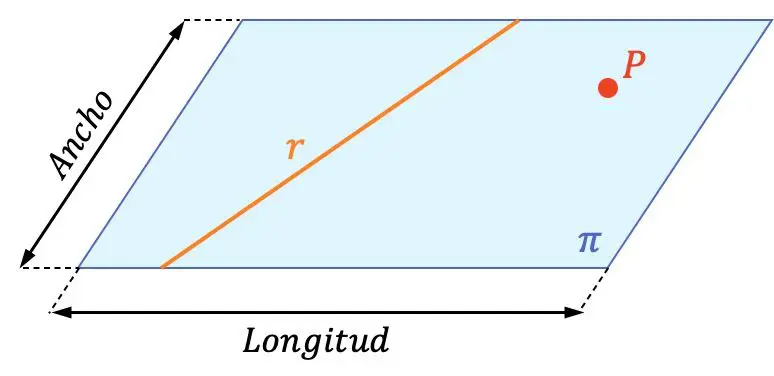
Bu nedenle bir düzlemde sonsuz çizgiler ve sonsuz noktalar bulunur. Yukarıdaki grafiksel gösterimde düzlem, çizgi ve nokta arasındaki farkı görebilirsiniz. Ayrıca satırın doğrulandığını da doğrulayabilirsiniz.
![]()
ve ipucu
![]()
düzlemin içinde bulunur
![]()
Grafikli planda da görebileceğiniz gibi planlar genellikle Yunanca harflerle adlandırılır:
![]()
Matematikte çok kullandığımız düzlem örneği Kartezyen düzlemdir. Kartezyen düzlem, apsis ekseni (X ekseni) ve ordinat ekseni (Y ekseni) tarafından tanımlanan düzlemdir. Kartezyen düzlemin kullanımlarından biri, bir nesnenin bir referans sistemindeki konumunu tanımlamak için kullanılmasıdır.
Bir plan belirlemek
Artık düzlemin anlamını gördüğümüze göre, üç boyutlu uzayda (R3’te) herhangi bir düzlemin nasıl belirlenebileceğini görelim.
Bir plan tamamen aşağıdaki geometrik unsurlar tarafından belirlenir:
- Üç nokta hizalanmamış.
- Düz bir çizgi ve dışarıda bir nokta.
- İki paralel çizgi veya iki kesişen çizgi.
Son noktaya gelince, muhtemelen iki doğrunun paralel olmasının ne anlama geldiğini zaten biliyorsunuzdur. Ancak sekant çizgilerinin anlamı daha az bilinmektedir, dolayısıyla herhangi bir sorunuz varsa burada sekant çizgilerinin ne olduğuna göz atabilirsiniz.
Dolayısıyla önceki 3 şarttan herhangi birine sahipsek plan yapabiliriz demektir.
plan özellikleri
Plan aşağıdaki özellikleri karşılamaktadır:
- Bir düzlemde sonsuz sayıda nokta bulunur.
- Bir düzlemde sonsuz sayıda çizgi bulunur.
- Uçak sınırsızdır, yani uzayda sınırsızca uzanan bir yüzeydir.
- Kesişen iki düzlem bir doğruyu belirler.
- Düzlemde bir noktası olan bir doğrunun orada bulunması zorunlu değildir. Bir doğrunun bir düzlemin parçası olabilmesi için bu düzlemde en az iki noktanın olması gerekir.
- Sonsuz düzlemler düz bir çizgiyi keser.
- Yarım düzlem, bir düzlemin kendi çizgilerinden biriyle kesildiğinde bölündüğü 2 parçanın her biri.
düzlem denklemleri
Analitik geometride bir düzlemin denklemi , herhangi bir düzlemin matematiksel olarak ifade edilmesini sağlayan bir denklemdir. Yani bir düzlemin denklemini bulmak için yalnızca bir noktaya ve o düzleme ait iki doğrusal bağımsız vektöre ihtiyacınız vardır.

Ancak yukarıda plan kavramının anlatımında gördüğümüz gibi plan belirlemenin birkaç yolu vardır. Aynı şekilde bir planı analitik olarak ifade etmenin de farklı yolları vardır.
Dolayısıyla düzlemin tüm denklem türleri şunlardır: vektör denklemi , parametrik denklemler , örtülü (veya genel) denklem ve düzlemin kanonik (veya segmental) denklemi .
Daha sonra planın tüm denklemlerinin açıklamasını ve formülünü detaylı olarak göreceğiz.
Düzlemin vektör denklemi
Bir düzlemin bir nokta ve iki yön vektörünü düşünün:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Bir düzlemin vektör denkleminin formülü şöyledir:
![]()
Veya eşdeğer:
![]()
Altın
![]()
Ve
![]()
iki skalerdir, yani iki gerçek sayıdır.
Düzlemin parametrik denklemleri
Bir düzlemin parametrik denkleminin formülü şöyledir:
![]()
Altın:
-
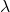
Ve
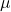
iki skalerdir, yani iki gerçek sayıdır.
-
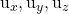
planın iki kılavuz vektöründen birinin bileşenleridir
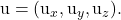
-
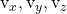
planın diğer yönlendirici vektörünün bileşenleridir
Düzlemin örtülü veya genel denklemi
Bir düzlemin bir nokta ve iki yön vektörünü düşünün:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Bir düzlemin örtülü, genel veya Kartezyen denklemi, aşağıdaki determinantın çözülmesi ve sonucun 0’a eşitlenmesiyle elde edilir:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Böylece ortaya çıkan planın örtülü veya genel denklemi aşağıdaki gibi olacaktır:
![]()
Bu tür düzlem denklemine Kartezyen düzlem denklemi de denir.
Düzlemin kanonik veya segmental denklemi
Bir düzlemin kanonik veya segmental denkleminin formülü aşağıdaki gibidir:
![]()
Altın:
-

düzlem ile X ekseni arasındaki kesişme noktasıdır.
-

düzlem ile Y ekseni arasındaki kesişme noktasıdır.
-

Düzlemin Z ekseniyle kesiştiği yer burasıdır.
Düzlemin kanonik denklemi (veya segmental denklemi) genel denkleminden de elde edilebilir:
![]()
İlk olarak D katsayısını denklemden çözüyoruz:
![]()
Daha sonra planın tüm denklemini D parametresinin değişen işaretinin değerine böleriz:
![]()
![]()
Kesirlerin özelliklerini kullanarak aşağıdaki ifadeye ulaşırız:
![]()
Dolayısıyla bu ifadeden bir düzlemin kanonik veya segmental denkleminin terimlerinin doğrudan hesaplanmasına izin veren formülleri çıkarıyoruz:
![]()
dolayısıyla plan denklemlerinin bu varyantını oluşturabilmek için A, B ve C katsayılarının sıfırdan farklı olması gerekir, böylece kesirlerdeki belirsizliklerden kaçınılır.
İki düzlemin göreceli konumu
Analitik geometride iki düzlem arasında yalnızca üç olası göreceli konum vardır: kesen düzlemler, paralel düzlemler ve çakışan düzlemler.
- Kesişen Düzlemler : İki düzlem yalnızca bir doğru üzerinde kesişiyorsa kesişiyor demektir.
- Paralel Düzlemler : İki düzlem herhangi bir noktada kesişmiyorsa paraleldir.
- Çakışmalı Düzlemler : İki düzlemin hepsinin ortak noktaları varsa çakışıktır.
kesişen düzlemler

paralel düzlemler

çakışan uçaklar

Ek olarak, eğer kesişen iki düzlem 90° açıyla kesişiyorsa, bunlar birbirine dik iki düzlemdir .
İki düzlem arasındaki açı
İki düzlem arasındaki açı, söz konusu düzlemlerin normal vektörlerinin oluşturduğu açıya eşittir. Bu nedenle iki düzlem arasındaki açıyı bulmak için normal vektörlerinin oluşturduğu açı hesaplanır, çünkü bunlar eşdeğerdir.
İki düzlem arasındaki açının tam olarak neyden oluştuğunu öğrendikten sonra, iki vektör arasındaki açı formülünden elde edilen, uzaydaki iki düzlem arasındaki açıyı hesaplama formülüne bakalım:
İki farklı düzlemin genel (veya örtülü) denklemi göz önüne alındığında:
![]()
![]()
Her düzlemin normal vektörü:
![]()
![]()
Ve bu iki düzlemin oluşturduğu açı, normal vektörlerinin oluşturduğu açı aşağıdaki formülle hesaplanarak belirlenir:
![]()
Açıkçası, iki düzlemin oluşturduğu açının kosinüsünü formülden hesapladıktan sonra, söz konusu açının değerini bulmak için kosinüsü ters çevirmemiz gerekir.
Öte yandan iki düzlem dik veya paralel olduğunda formülün uygulanmasına gerek yoktur çünkü 2 düzlem arasındaki açı doğrudan belirlenebilir:
- İki paralel düzlem arasındaki açı 0°’dir çünkü normal vektörleri aynı yöne sahiptir.
- İki dik düzlem arasındaki açı 90°’dir çünkü bunların normal vektörleri de birbirine diktir (veya diktir) ve bu nedenle bir dik açı oluşturur.