Bu sayfada plandaki tüm denklemlerin formüllerini ve nasıl hesaplandıklarını bulacaksınız. Ayrıca herhangi bir düzlemin normal vektörüyle denklemini nasıl bulacağınızı da keşfedeceksiniz. Ayrıca plan denklemlerinin örneklerini görebileceksiniz ve çözülmüş alıştırmalarla pratik yapabileceksiniz.
Düzlemin denklemi nedir?
Analitik geometride bir düzlemin denklemi , herhangi bir düzlemin matematiksel olarak ifade edilmesini sağlayan bir denklemdir. Yani bir düzlemin denklemini bulmak için yalnızca bir noktaya ve o düzleme ait iki doğrusal bağımsız vektöre ihtiyacınız vardır.
Düzlem denklemlerinin açıklanmasına devam etmeden önce düzlemin (geometri) ne olduğunu anlamanız önemlidir, aksi takdirde anlayamayacağınız şeyler olacaktır. Tamamen net değilseniz, plan hakkında bilmeniz gereken her şeyi topladığımız bu bağlantıya göz atabilirsiniz.
Planın denklemleri nelerdir?
Düzlem denkleminin tanımında gördüğümüz gibi, düz bir düzlem üzerindeki herhangi bir nokta, 1 nokta ve 2 vektörün doğrusal birleşimi olarak ifade edilebilir.

Ancak denklemin bir düzleme karşılık gelebilmesi için gerekli koşul, düzlemin iki vektörünün doğrusal bağımsızlığa sahip olmasıdır, yani iki vektör birbirine paralel olamaz.
Dolayısıyla, düzlemin tüm denklem türleri şunlardır: vektör denklemi , parametrik denklemler , örtülü (veya genel) denklem ve düzlemin kanonik (veya segmental) denklemi .
Daha sonra planın tüm denklemlerinin açıklamasını ve formülünü detaylı olarak göreceğiz.
Düzlemin vektör denklemi
Bir düzlemin bir nokta ve iki yön vektörünü düşünün:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Bir düzlemin vektör denkleminin formülü şöyledir:
![]()
Veya eşdeğer:
![]()
Altın
![]()
Ve
![]()
iki skalerdir, yani iki gerçek sayıdır.
Düzlemin parametrik denklemleri
Bir düzlemin parametrik denklemi onun vektör denkleminden belirlenebilir. Aşağıda demoyu görebilirsiniz.
Herhangi bir düzlemin vektör denklemi şöyle olsun:
![]()
Vektörlerin çarpımlarını skalerlerle çalıştırıyoruz ve ilk önce gerçekleştiriyoruz:
![]()
Daha sonra bileşenleri ekliyoruz:
![]()
Ve son olarak her değişkene karşılık gelen koordinatları ayrı ayrı özümleyerek planın parametrik denklemlerini elde ediyoruz:
![]()
Altın:
-
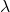
Ve
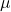
iki skalerdir, yani iki gerçek sayıdır.
-
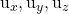
planın iki kılavuz vektöründen birinin bileşenleridir
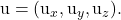
-
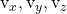
planın diğer yönlendirici vektörünün bileşenleridir
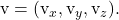
Düzlemin örtülü veya genel denklemi
Bir düzlemin bir nokta ve iki yön vektörünü düşünün:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Bir düzlemin örtülü, genel veya Kartezyen denklemi, aşağıdaki determinantın çözülmesi ve sonucun 0’a eşitlenmesiyle elde edilir:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Böylece ortaya çıkan planın örtülü veya genel denklemi aşağıdaki gibi olacaktır:
![]()
Bu tür düzlem denklemine Kartezyen düzlem denklemi de denir.
Düzlemin kanonik veya segmental denklemi
Bir düzlemin kanonik veya segmental denkleminin formülü aşağıdaki gibidir:
![]()
Altın:
-

düzlem ile X ekseni arasındaki kesişme noktasıdır.
-

düzlem ile Y ekseni arasındaki kesişme noktasıdır.
-

Düzlemin Z ekseniyle kesiştiği yer burasıdır.
Düzlemin kanonik denklemi (veya segmental denklemi) genel denkleminden de elde edilebilir:
![]()
İlk olarak D katsayısını denklemden çözüyoruz:
![]()
Daha sonra planın tüm denklemini D parametresinin değişen işaretinin değerine böleriz:
![]()
![]()
Kesirlerin özelliklerini kullanarak aşağıdaki ifadeye ulaşırız:
![]()
Dolayısıyla bu ifadeden bir düzlemin kanonik veya segmental denkleminin terimlerinin doğrudan hesaplanmasına izin veren formülleri çıkarıyoruz:
![]()
dolayısıyla plan denklemlerinin bu varyantını oluşturabilmek için A, B ve C katsayılarının sıfırdan farklı olması gerekir, böylece kesirlerdeki belirsizliklerden kaçınılır.
Bir düzlemin denklemi normal vektöründen nasıl hesaplanır
Düzlem denklemlerindeki çok tipik bir problem, verilen bir nokta ve onun normal (veya dik) vektörü verilen bir düzlemin denkleminin neye benzediğini bulmaktır. Peki nasıl çalıştığını görelim.
Ancak öncelikle bir düzleme dik vektörün X, Y, Z bileşenlerinin , söz konusu düzlemin örtülü (veya genel) denkleminin sırasıyla A, B, C katsayılarıyla çakıştığını bilmelisiniz.
![]()
Altın
![]()
vektör düzleme dik mi
![]()
Önceki ilişkiyi öğrendikten sonra, bu tür düzlem denklem problemlerini çözmenin bir örneğini görelim:
- Noktadan geçen düzlemin örtülü veya genel denklemini belirleyin
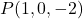
ve normal vektörlerinden biri
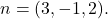
Bir düzlemin örtülü, genel veya Kartezyen denkleminin formülü şöyledir:
![]()
Böylece normal vektörden A, B ve C katsayılarını bulabiliriz çünkü bunlar normal vektörünün bileşenlerine eşdeğerdir:
![]()
Ancak sadece D parametresini bulmamız gerekiyor. Bunun için düzleme ait noktanın koordinatlarını denklemde yerine koyuyoruz:
![]()
![]()
![]()
![]()
![]()
Yani planın örtülü veya genel denklemi şöyledir:
![]()
Çözülmüş Düzlem Denklem Problemleri
1. Egzersiz
Vektörü içeren düzlemin vektör denklemini belirleyin
![]()
ve aşağıdaki iki noktadan geçer:
![]()
Ve
![]()
Bir düzlemin denklemini bilmek için bir noktaya ve iki vektöre ihtiyacınız vardır ve bu durumda elimizde yalnızca bir vektör vardır, dolayısıyla düzlemin başka bir yönlendirici vektörünü bulmamız gerekir. Bunu yapmak için düzlemin iki noktasını tanımlayan vektörü hesaplayabiliriz:
![]()
Artık düzlemin iki yön vektörünü ve bir noktayı zaten bildiğimize göre, düzlemin vektör denklemi formülünü kullanıyoruz:
![]()
Ve iki vektörü ve düzlemdeki iki noktadan birini denklemde yerine koyarız:
![]()
Alıştırma 2
Aşağıdaki üç noktayı içeren düzlemin parametrik denklemlerini bulun:
![]()
Düzlemin parametrik denklemlerini bulmak için düzlemde birbirine bağlanan iki doğrusal bağımsız vektör bulmamız gerekir. Bunun için de 3 noktayla tanımlanan iki vektörü hesaplayabiliriz:
![]()
![]()
Bulunan iki vektörün koordinatları orantılı olmadığından birbirlerinden doğrusal olarak bağımsızdırlar.
Artık iki yön vektörünü ve düzlemdeki bir noktayı zaten bildiğimize göre, düzlemin parametrik denklemi formülünü uyguluyoruz:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
Ve iki vektörü ve düzlemin üç noktasından birini denklemde yerine koyarız:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Alıştırma 3
Noktadan geçen düzlemin örtülü veya genel denklemini bulun
![]()
ve vektörleri içerir
![]()
Ve
![]()
Düzlemin genel veya örtülü denklemini hesaplamak için iki vektör, üç değişken ve noktanın koordinatlarından oluşan aşağıdaki determinantı çözmek gerekir:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Böylece vektörleri ve noktayı formülde yerine koyarız:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
Şimdi 3×3 matrisin determinantını seçtiğiniz yöntemle çözüyoruz:
![]()
Son olarak işlemleri gerçekleştirip benzer terimleri gruplandırıyoruz:
![]()
![]()
![]()
Yani planın örtülü veya genel denklemi şöyledir:
![]()
Alıştırma 4
Noktanın olup olmadığını belirleyin
![]()
aşağıdaki plana aittir:
![]()
Noktanın düzlemde olabilmesi için denkleminin doğrulanması gerekir. Bu nedenle, noktanın Kartezyen koordinatlarını düzlem denkleminde yerine koymamız ve denklemin yerine getirilip getirilmediğini kontrol etmemiz gerekir:
![]()
![]()
![]()
![]()
![]()
Nokta düzlemin denklemine uymadığından bu düzlemin parçası değildir.
Alıştırma 5
Genel (veya örtülü) denklemi aşağıdaki gibi olan düzlemin segmental denklemini bulun:
![]()
Öncelikle bağımsız terimi denklemden siliyoruz:
![]()
Daha sonra planın tüm denklemini D değişen işaretinin değerine böleriz:
![]()
![]()
Kesirlerin özelliklerini kullanarak aşağıdaki ifadeye ulaşırız:
![]()
Dolayısıyla düzlemin segmental (veya kanonik) denklemi şöyledir:
![]()
Alıştırma 6
Uzayda noktadan geçen düzlemin örtülü veya genel denklemini hesaplar
![]()
ve normal vektörlerinden biri
![]()
Bir düzlemin örtülü, genel veya Kartezyen denkleminin formülü şöyledir:
![]()
Normal vektörden A, B ve C katsayılarını bulabiliriz çünkü bunlar sırasıyla normal vektörün bileşenlerine eşittir:
![]()
Yani sadece D parametresini bulmamız gerekiyor. Bunu yapmak için düzleme ait noktanın koordinatlarını denklemde yerine koyuyoruz:
![]()
![]()
![]()
![]()
![]()
Sonuç olarak planın örtülü veya genel denklemi şöyledir:
![]()
Egzersiz 7
Doğruyu içeren düzlemin parametrik denklemlerini bulun
![]()
ve sağa paralel
![]()
çizgiler olmak üzere:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Düzlemin parametrik denklemlerini bulmak için iki yön vektörünü ve düzlem üzerindeki bir noktayı bilmemiz gerekir. Bildirim bize satırı içerdiğini söylüyor
![]()
Dolayısıyla düzlemi tanımlamak için yön vektörünü ve bu doğru üzerindeki bir noktayı alabiliriz. Ayrıca bu ifade bize düzlemin doğruya paralel olduğunu söyler.
![]()
yani bu doğrunun yön vektörünü düzlem denklemi için de kullanabiliriz.
doğru
![]()
parametrik denklemler biçiminde ifade edilir, dolayısıyla yön vektörünün bileşenleri parametre terimlerinin katsayılarıdır.
![]()
![]()
Aynı çizgi üzerindeki bir noktanın Kartezyen koordinatları da parametrik denklemlerin bağımsız terimleridir:
![]()
Öte yandan düz çizgi
![]()
yön vektörünün bileşenleri kesirlerin paydaları olacak şekilde sürekli bir denklem biçimindedir:
![]()
Bu nedenle planın parametrik denklemleri şöyledir:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)