Doğrunun kanonik, segmental veya simetrik denklemi

Burada, simetrik denklem olarak da adlandırılan doğrunun kanonik (veya parçalı) denkleminin formülünün ne olduğuna ilişkin açıklamayı bulacaksınız. Ayrıca örnekleri görebilecek ve çözümlü alıştırmalarla pratik yapabileceksiniz. Ve hatta kanonik denklemin, doğrunun genel (veya örtülü) denkleminden nasıl hesaplandığını bulacaksınız.

Doğrunun kanonik veya segmental denklemi nedir?

Bir çizginin matematiksel tanımının, eğriler veya açılar olmadan aynı yönde temsil edilen ardışık noktalar kümesi olduğunu unutmayın.

Dolayısıyla, çizginin parçalı denklemi olarak da adlandırılan çizginin kanonik denklemi, herhangi bir çizgiyi matematiksel olarak ifade etmenin bir yoludur. Bunun için söz konusu doğrunun koordinat eksenleriyle kesiştiği noktaların bilinmesi yeterlidir.

Öte yandan analitik geometride doğrunun kanonik (veya segmental) denklemine doğrunun simetrik denklemi de denir.

Çizginin kanonik veya segmental denkleminin formülü

Doğrunun kanonik veya segmental denklemi, doğrunun x ekseni ve y eksenini kestiği yerdeki değerlerin bilinmesiyle belirlenebilen doğrunun cebirsel ifadesidir.

Bir çizgi Kartezyen eksenlerini aşağıdaki noktalarda keserse:

X ekseni ile kesişme noktası:

$(a,0)$

Y ekseni ile kesişme noktası:

$(0,b)$

Doğrunun kanonik (veya segmental) denkleminin formülü şöyledir:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

uzaydaki çizginin segmental veya simetrik kanonik denklemi

Aşağıdaki üç durumun hiçbirinde çizginin kanonik (veya segmental) denkleminin bulunmadığına dikkat edilmelidir:

Çizgi dikey olduğunda, yani OY eksenine paralel olduğunda. Çünkü dikey bir doğrunun denklemi
$x=k.$
Çizgi yatay olduğunda, yani OX eksenine paralel olduğunda. Çünkü yatay bir doğrunun denklemi
$y=k.$
Çizgi koordinat orijininden geçtiğinde (nokta
$(0,0)$

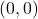
), çünkü o zaman doğrunun denkleminde iki belirsizliğimiz olur.

Doğrunun kanonik veya segmental denkleminin nasıl bulunacağına ilişkin örnek

Konsepti daha iyi anlamanız için doğrunun parçalı (veya kanonik) denklem problemini çözeceğiz:

Aşağıdaki iki noktadan geçen doğrunun kanonik veya segmental denklemini bulun:

$A(0,4) \qquad \qquad B(-2,0)$

Bu durumda beyan bize 2 puanı değil, eksenlerle kesişen iki noktayı verir.

Doğrunun X ekseniyle kesişme noktası:

$(-2,0)$

Doğrunun Y ekseniyle kesişme noktası:

$(0,4)$

Dolayısıyla, eksenlerle kesişen iki noktayı zaten bildiğimiz için, doğrunun kanonik veya segmental denklemi için formülü uygulamamız yeterlidir:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Ve son olarak parametrelerin değerini değiştiriyoruz

$a$

$b$

formülde:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{4}}\bm{= 1}$

Artık doğrunun kanonik (veya segmental) denkleminin ne olduğunu biliyorsunuz. Ancak bir doğruyu ifade etmenin başka yollarının da olduğunu ve bunların arasında açık denklemin öne çıktığını bilmelisiniz. Bu tür çizgi denklemini tam olarak anlamak zordur, bu nedenle ilgili her şeyi bağlantılı sayfada ayrıntılı olarak açıkladık.

Doğrunun kanonik veya segmental denklemini genel denkleminden hesaplayın

Doğrunun kanonik veya segmental denklemini belirlemenin bir yolunu gördük, ancak başka yöntemler de var:

Bir doğrunun kanonik veya segmental denklemi, aynı doğrunun genel (veya örtülü) denkleminden elde edilebilir:

$Ax+By+C=0$

Öncelikle C katsayısında taraf değiştiriyoruz:

$Ax+By=-C$

Daha sonra, denklemin tamamını işareti değişen C parametresinin değerine bölüyoruz:

$\cfrac{Ax+By}{-C}=\cfrac{-C}{-C}$

$\cfrac{Ax}{-C}+\cfrac{By}{-C}=1$

Ve kesirlerin özellikleri aracılığıyla doğrunun kanonik veya segmental denkleminin formülüne ulaşıyoruz:

$\cfrac{x}{-\frac{C}{A}}+\cfrac{y}{-\frac{C}{B}}=1$

Dolayısıyla bu formülden şu terimler çıkıyor:

$a$

$b$

Bir doğrunun kanonik denkleminin denklemi aşağıdaki ifadelere eşdeğerdir:

$a= -\cfrac{C}{A} \qquad \qquad b= -\cfrac{C}{B}$

Çizginin kanonik veya segmental denkleminin çözülmüş problemleri

1. Egzersiz

Aşağıdaki doğrunun koordinat eksenleriyle kesişme noktaları nelerdir?

$\cfrac{x}{3}+ \cfrac{y}{-1}= 1$

Çözüme bakın

Alıştırmadaki çizgi, formülü aşağıdaki gibi olan çizginin kanonik veya segmental denklemi biçiminde ifade edilir:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Buna göre doğrunun koordinat eksenlerini kestiği noktalar şunlardır:

X ekseni ile kesişme noktası:

$\bm{(3,0)}$

Y ekseni ile kesişme noktası:

$\bm{(0,-1)}$

Alıştırma 2

Grafiği çizilen çizginin kanonik veya segmental denklemi nedir?

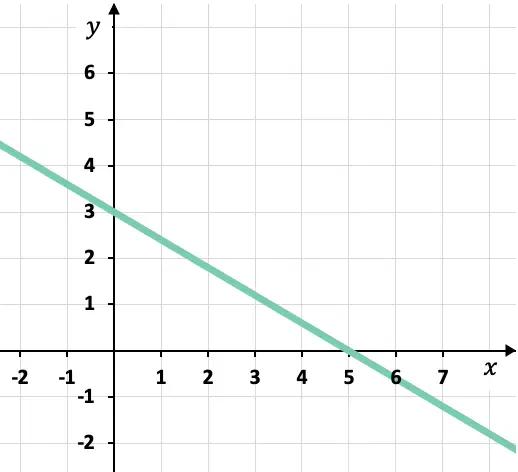
düzlemde segmental veya simetrik kanonik denklem

Çözüme bakın

Grafikten çizginin koordinat eksenlerini kestiği noktaları bilebiliriz:

Doğrunun X ekseniyle kesişme noktası:

$(5,0)$

Doğrunun Y ekseniyle kesişme noktası:

$(0,3)$

Dolayısıyla, eksenlerle kesişen 2 noktayı zaten bildiğimizde, doğrunun kanonik veya segmental denklemi için formülü kullanmamız yeterlidir:

$\cfrac{x}{a}+ \cfrac{y}{b}= 1$

Ve son olarak parametrelerin değerini değiştiriyoruz

$a$

$b$

formülde:

$\cfrac{\bm{x}}{\bm{5}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Alıştırma 3

Aşağıdaki genel (veya örtülü) denklemle belirlenen çizginin kanonik veya segmental denklemini hesaplayın:

$3x-2y+6=0$

Çözüme bakın

Genel bir denklemden parçalı bir denkleme geçmek için önce denklemin bağımsız terimini izole etmeliyiz:

$3x-2y+6=0$

$3x-2y=-6$

İkinci olarak denklemin tamamını denklemin sağ tarafındaki katsayıya bölüyoruz:

$\cfrac{3x-2y}{-6}=\cfrac{-6}{-6}$

$\cfrac{3x}{-6}+\cfrac{-2y}{-6}=\cfrac{-6}{-6}$

Yukarıdaki ifade aşağıdakine eşdeğerdir:

$\cfrac{x}{\frac{-6}{3}}+\cfrac{y}{\frac{-6}{-2}}=1$

Böylece doğrunun kanonik, segmental veya simetrik denklemi şöyle olur:

$\cfrac{\bm{x}}{\bm{-2}}\bm{+} \cfrac{\bm{y}}{\bm{3}}\bm{= 1}$

Alıştırma 4

Yön vektörü olan kanonik veya segmental denklemi belirleyin.

$\vv{\text{v}}=(4,-3)$

ve noktadan geçer

$P(-1,5).$

Çözüme bakın

Öncelikle doğrunun sürekli denklemini yön vektöründen ve doğruya ait bir noktadan kolaylıkla buluruz:

$\cfrac{x-P_1}{\text{v}_1} = \cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{4} = \cfrac{y-5}{-3}$

$\cfrac{x+1}{4} = \cfrac{y-5}{-3}$

Şimdi kesirleri çapraz olarak çarparak ve elde edilen terimleri gruplandırarak doğrunun genel denklemini hesaplayalım:

$-3(x+1) = 4(y-5)$

$-3x-3 = 4y-20$

$-3x-3 - 4y+20 =0$

$-3x - 4y+17 =0$

Bu nedenle doğrunun genel denklemini kanonik bir denkleme dönüştürmek yeterlidir. Bunu yapmak için önce bağımsız terimi denklemden siliyoruz:

$-3x - 4y=-17$

Daha sonra denklemin tamamını denklemin sağ tarafındaki katsayıya bölüyoruz:

$\cfrac{-3x - 4y}{-17}=\cfrac{-17}{-17}$

$\cfrac{-3x}{-17}+\cfrac{-4y}{-17}=\cfrac{-17}{-17}$

Yukarıdaki ifade aşağıdakine eşdeğerdir:

$\cfrac{x}{\frac{-17}{-3}}+\cfrac{y}{\frac{-17}{-4}}=1$

Negatifin negatife bölümü pozitife eşittir:

$\cfrac{x}{\frac{17}{3}}+\cfrac{y}{\frac{17}{4}}=1$

Kesirler daha fazla basitleştirilemez, bu nedenle doğrunun kanonik, segmental veya simetrik denklemi şöyledir:

$\cfrac{\bm{x}}{\mathbf{\frac{17}{3}}}\bm{+} \cfrac{\bm{y}}{\mathbf{\frac{17}{4}}}\bm{= 1}$

Doğrunun kanonik veya segmental denklemi nedir?

Çizginin kanonik veya segmental denkleminin formülü

Doğrunun kanonik veya segmental denkleminin nasıl bulunacağına ilişkin örnek

Doğrunun kanonik veya segmental denklemini genel denkleminden hesaplayın

Çizginin kanonik veya segmental denkleminin çözülmüş problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et