Eş düzlemli (veya eş düzlemli) noktalar

Bu sayfada eş düzlemli (veya eş düzlemli) noktaların ne olduğunu ve belirli noktaların eş düzlemli olup olmadığını nasıl anlayacağınızı keşfedeceksiniz. Ayrıca örnekleri görebileceksiniz ve çözülmüş eşdüzlemli noktalar alıştırmaları ile pratik yapabileceksiniz.

Eş düzlemli noktalar nelerdir?

Analitik geometride eş düzlemli (veya eş düzlemli) noktaların anlamı aşağıdaki gibidir:

Eş düzlemli noktalar aynı düzleme ait noktalardır.

Bu nedenle, 2 veya 3 nokta her zaman aynı düzlemdedir çünkü bir düzlem en az 3 noktadan oluşturulabilir. Öte yandan 4, 5 veya daha fazla nokta olduğunda bazı noktaların aynı düzlemde bulunmaması ve dolayısıyla eş düzlemli olmaması da mümkündür.

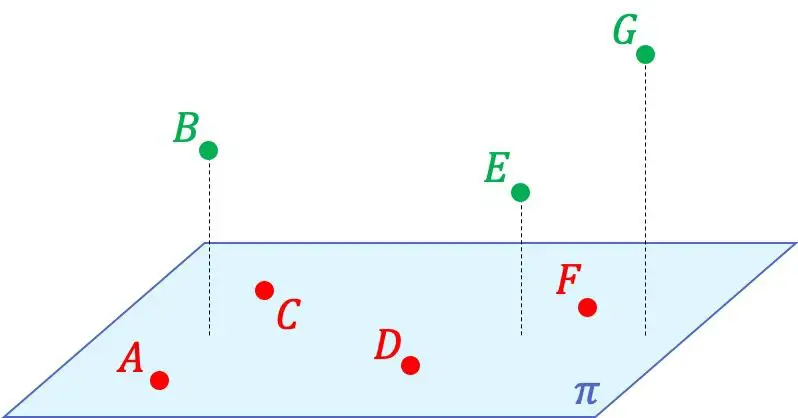
Örneğin yukarıdaki grafik gösterimde A, C, D ve F noktalarının aynı düzlemde yer almaları nedeniyle birbirleriyle eş düzlemli olduklarını görebilirsiniz. Öte yandan bu 4 nokta B, E ve G noktalarıyla eş düzlemli değildir çünkü bu noktaların bulunduğu uzayda herhangi bir düzlem oluşamaz.

Bu özellikten eş düzlemli noktalarla tanımlanan vektörlerin aynı zamanda eş düzlemli vektörler olduğu, yani aynı düzlemde yer aldıkları sonucunu çıkarabiliriz.

Noktalar ne zaman eş düzlemlidir?

Eş düzlemli (veya eş düzlemli) noktaların tanımında gördüğümüz gibi, iki veya üç nokta her zaman eş düzlemlidir, ancak üçten fazla noktanın eş düzlemlilik ilişkisine uyması gerekmez.

Dolayısıyla, dört veya daha fazla noktanın aynı düzlemde olup olmadığını belirlemek için esas olarak 2 yöntem vardır:

Noktaların eş düzlemli olup olmadığını bilmenin bir yolu, noktalar tarafından belirlenen vektörlere bakmaktır: eğer bu vektörler eş düzlemli ise , o zaman noktalar da eş düzlemlidir.

Açıkçası, bu yöntemi uygulamak için vektörlerin ne zaman eş düzlemli olduğunu bilmeniz gerekir. Ancak bir vektör kümesinin eş düzlemli olup olmadığını belirlemenin de birkaç yolu olduğundan, vektörlerin eş düzlemli olup olmadığını nasıl anlayacağınızı kontrol etmenizi öneririz. Burada 2, 3, 4 veya daha fazla vektörün eş düzlemli olduğunu bulmak için mevcut tüm prosedürlerin yanı sıra örnekler ve çözülmüş alıştırmalar bulacaksınız.

Bir nokta kümesinin eş düzlemli olup olmadığını anlamanın bir başka yolu da kümedeki 3 noktanın oluşturduğu düzlemin denklemini bulmaktır ve diğer noktalar bu denklemi sağlıyorsa bu, kümedeki tüm noktaların eş düzlemli olduğu anlamına gelir.

Soruna bağlı olmasına rağmen, iki yöntemden ilkinin kullanılmasını öneririz çünkü vektörlerin eş düzlemli olup olmadığını kontrol etmek bir düzlemin denklemini hesaplamaktan çok daha basit ve hızlıdır. Ama elbette hangisini tercih ederseniz onu kullanın.

Çözülmüş eş düzlemli nokta problemleri

1. Egzersiz

Aşağıdaki üç noktanın aynı düzlemde olup olmadığını belirleyin:

$A(3,5,1)$

$B(0,-2,3)$

$C(4,-1,2)$

Çözüme bakın

Bu durumda herhangi bir hesaplama yapmaya gerek yoktur çünkü ne olursa olsun 3 nokta her zaman aynı düzlemdedir .

Alıştırma 2

Aşağıdaki dört noktanın eş düzlemli olup olmadığını belirleyin:

$A(1,2,0)$

$B(-1,3,4)$

$C(1,0,-1)$

$D(2,5,-3)$

Çözüme bakın

Dört noktanın eş düzlemli olması için, onlar tarafından belirlenen vektörlerin eş düzlemli olması gerekir. Bu nedenle bu vektörleri hesaplıyoruz:

$\vv{AB} = B- A = (-1,3,4)-(1,2,0) = (-2,1,4)$

$\vv{AC} = C- A = (1,0,-1)-(1,2,0) = (0,-2,-1)$

$\vv{AD} = D- A = (2,5,-3)-(1,2,0) = (1,3,-3)$

Şimdi vektörlerin oluşturduğu matrisi oluşturalım:

$\displaystyle A= \begin{pmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{pmatrix}$

Ortaya çıkan vektörlerin eş düzlemli olması için önceki matrisin rütbesinin 2’ye eşit olması gerekir. Bunun için de 3×3 matrisin tamamının determinantının sıfıra eşit olması gerekir:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -2&1&4 \\[1.1ex]0&-2&-1 \\[1.1ex] 1&3&-3\end{vmatrix} =-11\neq 0$

$rg(A)=3$

Ancak tüm matrisin determinantı sıfırdan farklı olduğundan matrisin rütbesi 3’tür ve bu nedenle 4 nokta eş düzlemli değildir .

Alıştırma 3

Aşağıdaki beş noktanın eş düzlemli olup olmadığını öğrenin:

$A(3,1,1)$

$B(0,0,2)$

$C(4,-2,-1)$

$D(-1,1,3)$

$E(2,4,3)$

Çözüme bakın

Beş noktanın hepsinin eş düzlemli olması için, onlar tarafından tanımlanan vektörlerin eş düzlemli olması gerekir. Bu nedenle bu vektörleri hesaplıyoruz:

$\vv{AB} = B- A = (0,0,2)-(3,1,1) = (-3,-1,1)$

$\vv{AC} = C- A = (4,-2,-1)-(3,1,1) = (1,-3,-2)$

$\vv{AD} = D- A = (-1,1,3)-(3,1,1) = (-4,0,2)$

$\vv{AE} = E- A = (2,4,3)-(3,1,1) = (-1,3,2)$

Şimdi vektörlerden oluşan matrisi oluşturalım:

$\displaystyle A= \begin{pmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{pmatrix}$

Ortaya çıkan vektörlerin eş düzlemli olması için, önceki matrisin sırasının 2’ye eşit olması gerekir. Bu nedenle, eş düzlemli olup olmadıklarını kontrol etmek için vektörlerin matrisinin sırasını determinantlara göre hesaplıyoruz:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -4&0&2\end{vmatrix} = 0 \qquad \begin{vmatrix} -3&-1&1 \\[1.1ex]1&-3&-2 \\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1&1 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0 \qquad \begin{vmatrix} 1&-3&-2 \\[1.1ex] -4&0&2\\[1.1ex] -1&3&2\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} -3&-1 \\[1.1ex] 1&-3\end{vmatrix} =10\neq 0$

$rg(A)=2$

Matrisin rütbesi 2’ye eşdeğerdir, dolayısıyla vektörler eş düzlemlidir ve bu nedenle 5 nokta da eş düzlemlidir.

Alıştırma 4

Parametre değerini hesapla

$k$

böylece aşağıdaki 4 nokta aynı düzlemdedir:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

Çözüme bakın

Dört noktanın eş düzlemli olması için, onlar tarafından belirlenen vektörlerin eş düzlemli olması gerekir. Bu nedenle bu vektörleri hesaplıyoruz:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Kimin vektör matrisi:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Ortaya çıkan vektörlerin eş düzlemli olması için matrisin rütbesinin 2 olması gerekir. Dolayısıyla 3×3’lük matrisin tamamının determinantı 0 olmalıdır:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$

$\displaystyle 2k-3 =0$

Sonunda bilinmeyeni çözüyoruz

$k:$

$2k =3$

$\bm{k =}\mathbf{\cfrac{3}{2}}$

Son olarak, eğer bu makale sizin için yararlı olduysa, muhtemelen iki nokta arasındaki mesafenin nasıl hesaplandığı (formül) ile de ilgileniyorsunuzdur, çünkü bazen analitik geometri problemlerinde bize iki nokta arasındaki mesafenin ne olduğu sorulur. Bağlantılı sayfada çok ayrıntılı bir açıklamanın yanı sıra adım adım çözülen örnekler ve alıştırmalar bulacaksınız.

Eş düzlemli noktalar nelerdir?

Noktalar ne zaman eş düzlemlidir?

Çözülmüş eş düzlemli nokta problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et