Eş düzlemli (veya eş düzlemli) vektörler

Bu sayfada eş düzlemli vektörlerin ne olduğunu ve 2, 3, 4 veya daha fazla vektörün eş düzlemli olup olmadığını nasıl anlayacağınızı öğreneceksiniz. Ayrıca eş düzlemli vektörlerin adım adım çözüldüğü örnekleri ve alıştırmaları görebileceksiniz.

Eş düzlemli vektörler nelerdir?

Analitik geometride eş düzlemli (veya eş düzlemli) vektörlerin anlamı aşağıdaki gibidir:

Eş düzlemli vektörler aynı düzleme ait olan vektörlerdir.

Bu nedenle, iki vektör her zaman aynı düzlemdedir çünkü bir düzlem en az 2 vektörle oluşturulabilir. Öte yandan, 3, 4 veya daha fazla vektör olduğunda, vektörlerden birinin aynı düzlemde yer almaması ve dolayısıyla eş düzlemli olmaması mümkündür.

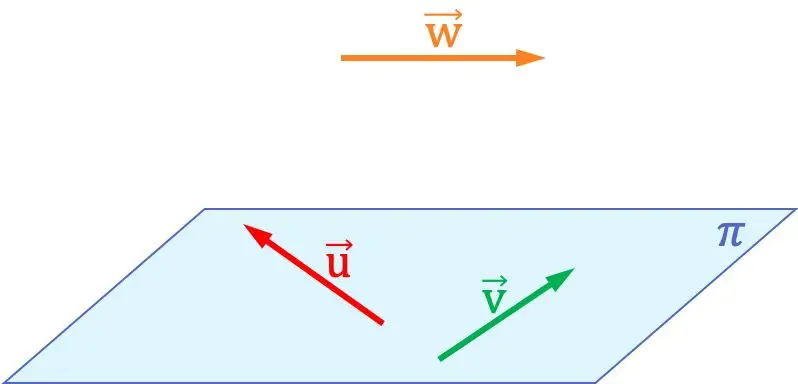
eş düzlemli veya eş düzlemli vektör örnekleri

Örneğin, yukarıdaki grafikte vektörlerin olduğunu görebilirsiniz.

$\vv{\text{u}}$

$\vv{\text{v}}$

aynı düzlemde bulundukları için birbirleriyle eş düzlemlidirler. Öte yandan bu iki vektör, vektörle aynı düzlemde değildir.

$\vv{\text{w}}$

Çünkü üç vektörün bulunduğu uzayda hiçbir düzlem oluşamaz.

Bu özellikten, eğer 3 veya daha fazla vektör eş düzlemli ise, söz konusu vektörleri tanımlayan noktaların (vektörün başlangıç ve bitişi) aynı düzlemde noktalar olduğu sonucunu çıkarabiliriz.

Vektörler ne zaman eş düzlemlidir?

Eş düzlemli (veya eş düzlemli) vektörlerin tanımında gördüğümüz gibi, iki vektör her zaman eş düzlemlidir, ancak ikiden fazla vektörün eş düzlemlilik ilişkisine uyması gerekmez.

Bu nedenle, üç veya daha fazla vektörün eş düzlemli olup olmadığını belirlemek için çeşitli yöntemler vardır:

Üç vektörün (veya üçlü nokta çarpımının) karışık çarpımı sıfıra eşitse, bu, üç vektörün aynı düzlemde olduğu anlamına gelir. Bu işlemin nasıl hesaplandığı konusunda çok net değilseniz, üç vektörün karma çarpımının ne olduğuna bir göz atmanızı öneririm, burada açıklamanın yanı sıra örnekler ve çözülmüş alıştırmalar da bulacaksınız.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] =0$

Bir vektör kümesi , iki vektörün doğrusal birleşimi olarak ifade edilebiliyorsa, bu onların eş düzlemli oldukları anlamına gelir, yani 3 veya daha fazla vektör ancak ve ancak doğrusal olarak bağımlı olduklarında eş düzlemlidir. Üç veya daha fazla vektörün iki vektörün doğrusal birleşimi olduğunu göstermek için tüm vektörlerin oluşturduğu matrisin rütbesinin 2’ye eşit olması yeterlidir.

$rg(A) = 2$

Doğrusal bağımlılık ve bağımsızlık kavramını, yani iki vektörün doğrusal olarak bağımlı veya doğrusal olarak bağımsız olmasını ve bunun ne anlama geldiğini iyi anlamanız önemlidir. Tamamen net değilseniz, bağlantıda çok ayrıntılı bir açıklama bulacaksınız, ayrıca adım adım çözülmüş örnekleri ve alıştırmaları da görebilirsiniz.

Söz konusu vektörler paralel vektörler ise, bu aynı zamanda eş düzlemli oldukları, yani tüm paralel vektörlerin aynı düzlemde yer aldığı anlamına gelir.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Eş düzlemli vektörlerin çözülmüş sorunları

1. Egzersiz

Aşağıdaki üç vektörün eş düzlemli olup olmadığını belirleyin:

$\vv{\text{u}} = (3,1,2)$

$\vv{\text{v}} = (2,3,-1)$

$\vv{\text{w}} = (-1,-5,4)$

Çözüme bakın

Bunların 3 eş düzlemli vektör olup olmadığını kontrol etmek için üç vektör arasındaki karışık çarpımı hesaplamamız gerekir:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}$

Üç vektörün karışık çarpımı sıfırdır, dolayısıyla 3 vektör aynı düzlemdedir .

Alıştırma 2

Aşağıdaki üç vektörün eş düzlemli olup olmadığını belirleyin:

$\vv{\text{u}} = (4,-2,6)$

$\vv{\text{v}} = (-2,1,-3)$

$\vv{\text{w}} = (6,-3,9)$

Çözüme bakın

3 eş düzlemli vektörle ilgilenip ilgilenmediğimizi kontrol etmenin bir yolu, üç vektör arasındaki karışık çarpımı çözmek olacaktır. Ancak vektörlerin bileşenlerine yakından baktığımızda orantılı olduklarını görebiliriz. Bu nedenle üç vektör birbirine paraleldir.

$\vv{\text{u}} \parallel \vv{\text{v}} \parallel \vv{\text{w}}$

Ve tüm vektörler paralel olduğundan, bunlar aslında 3 eş düzlemli vektördür .

Alıştırma 3

Aşağıdaki dört vektörün eş düzlemli olup olmadığını belirleyin:

$\vv{\text{a}} = (2,1,1)$

$\vv{\text{b}} = (1,-1,2)$

$\vv{\text{c}} = (-1,0,-1)$

$\vv{\text{d}} = (3,1,2)$

Çözüme bakın

Dört vektörün eş düzlemli olup olmadığını bilmek için tüm vektörlerden oluşan matrisin sıralamasını hesaplamamız gerekir:

$\displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}$

Bu durumda söz konusu matrisin kapsamını belirleyicilere göre hesaplıyoruz:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0$

$\displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0$

$rg(A) = 2$

Tüm vektörlerin oluşturduğu matrisin rütbesi 2’ye eşdeğerdir, dolayısıyla 4 vektör aynı düzlemdedir .

Alıştırma 4

Parametre değerini hesapla

$k$

böylece aşağıdaki 4 nokta aynı düzlemdedir:

$A(3,1,4)$

$B(2,1,2)$

$C(0,-1,3)$

$D(3,2,k)$

Çözüme bakın

Dört noktanın eş düzlemli olması için, onlar tarafından belirlenen vektörlerin eş düzlemli olması gerekir. Bu nedenle bu vektörleri hesaplıyoruz:

$\vv{AB} = B- A = (2,1,2)-(3,1,4) = (-1,0,-2)$

$\vv{AC} = C- A = (0,-1,3)-(3,1,4) = (-3,-2,-1)$

$\vv{AD} = D- A = (3,2,k)-(3,1,4) = (0,1,k-4)$

Kimin vektör matrisi:

$\displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}$

Ortaya çıkan vektörlerin eş düzlemli olması için matrisin rütbesinin 2 olması gerekir. Dolayısıyla 3×3’lük matrisin tamamının determinantı 0 olmalıdır:

$\displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0$