Uzayda iki çizgi arasındaki mesafe (R3'te)

Bu sayfada, türleri ne olursa olsun (paralel, kesen, çakışan, kesen, dik doğrular vb.) uzayda iki doğru arasındaki mesafenin nasıl hesaplandığını (R3’te) bulacaksınız. Ayrıca adım adım çözülen örnekleri ve alıştırmaları görebileceksiniz.

İki çizgi arasındaki mesafe nasıl hesaplanır

İki çizgi arasındaki mesafe, bir çizgideki herhangi bir nokta ile diğer çizgideki herhangi bir nokta arasındaki minimum mesafedir. Bu mesafe, bir doğrudan diğer doğruya giden ve aynı zamanda her iki doğruya da dik olan doğru parçasının uzunluğuna karşılık gelir.

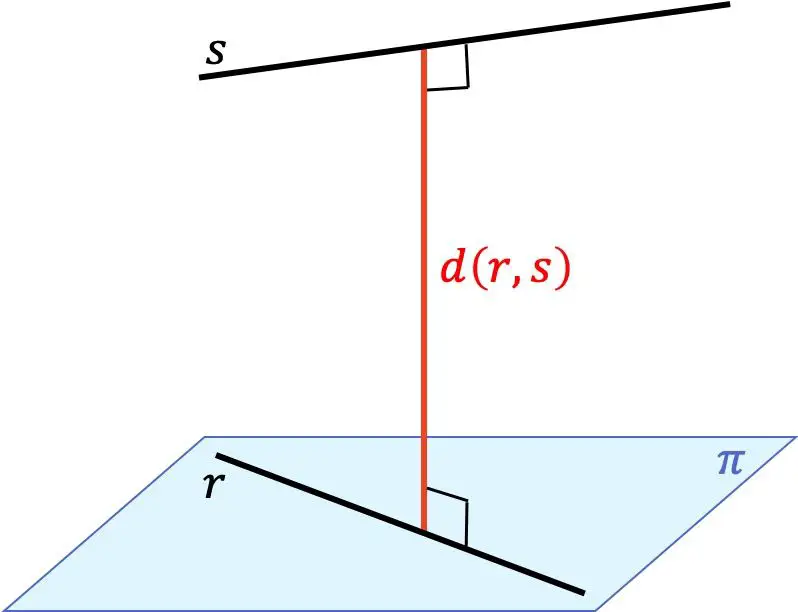
uzayda iki çizgi arasındaki mesafe (R3'te)

Dolayısıyla, üç boyutlu (3B) uzayda iki farklı çizgi arasındaki mesafeyi bulmak, aralarındaki göreceli konuma bağlıdır:

İki çizgi çakışırsa veya kesişirse , iki çizgi arasındaki mesafe sıfırdır çünkü bunlar (en azından) bir noktada kesişir.
İki doğru paralel olduğunda doğrulardan birinin üzerindeki herhangi bir noktayı alıp o nokta ile diğer doğru arasındaki mesafeyi hesaplamamız gerekir (aşağıda bunun nasıl yapılacağına dair bir örnek verilmiştir).
Eğer iki çizgi uzayda kesişiyorsa , kesişen iki çizgi arasındaki mesafe formülünü uygulamamız gerekir (detaylı açıklama için aşağıya bakınız).

Bu nedenle, iki çizgi arasındaki mesafeyi hesaplamak için öncelikle bunların ne tür çizgiler olduğunu bilmeniz ve ardından duruma bağlı olarak şu veya bu formülü kullanmanız gerekir. Bu nedenle, devam etmeden önce uzayda iki çizginin göreceli konumunu nasıl bulacağınızı zaten öğrenmeniz önemlidir, ancak bunun nasıl yapıldığını hatırlamıyorsanız, bağlantıda çok eksiksiz bir açıklamanın yanı sıra çözülmüş örnekler ve alıştırmalar göreceksiniz. adım adım.

Uzayda iki paralel çizgi arasındaki mesafe nasıl bulunur?

Uzayda (R3’te) iki paralel çizgi arasındaki mesafenin hesaplanması, düzlemde (R2’de) olduğu gibi yapılır: iki doğrunun herhangi birinde bir nokta almanız ve diğerinde bu noktanın mesafesini bulmanız gerekir. astar.

Dolayısıyla, bir noktadan bir çizgiye olan mesafeyi 3 boyutlu olarak hesaplamak için (ve iki paralel çizgi arasındaki mesafeyi belirlemek için kullanılan) formül şöyledir:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Altın:

$\lvert \vv{\text{v}}_r \rvert$

çizginin yön vektörünün büyüklüğüdür

$r.$
$Q$

çizgi üzerinde bir noktadır

$r,$

$P$

çizgi üzerinde bir nokta

$s$

Ve

$\vv{QP}$

iki nokta tarafından tanımlanan vektör
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

vektörler arasındaki çapraz çarpımın büyüklüğüdür

$\vv{QP}$

Ve

$\vv{\text{v}}_r$

Örnek olarak uzaydaki 2 paralel doğru arasındaki mesafe problemini çözeceğiz:

Aşağıdaki iki paralel çizgi arasındaki mesafe nedir?

$r: \ (x,y,z) = (2,1,1) + t(-1,3,2)$

$s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)$

Her iki çizgi de bir vektör denklemi biçiminde ifade edilir, bu nedenle yön vektörünü ve her birinin bir noktasını kolayca bulabiliriz:

$\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}$

Bir doğrunun yön vektörünün ve bir noktasının nasıl belirleneceği konusunda şüpheleriniz varsa, doğrunun denklemi açıklamasına göz atmanızı öneririz. Orada bunu doğrunun tüm denklemleri için açıkladık çünkü bir doğruya ait yön vektörünü ve bir noktayı bulmak, o doğrunun ifade edildiği denklemin türüne bağlıdır.

Şimdi iki paralel çizgi arasındaki mesafeyi bulmak için bir noktadan bir çizgiye olan mesafe formülünü uygulamamız gerekiyor:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

Yani bir yandan vektör çarpımından elde edilen vektörün modülünü hesaplıyoruz. Nasıl hesaplandığı konusunda şüpheniz varsa, vektör çarpım formülüne başvurabilirsiniz; burada ayrıca vektörler arasındaki bu işlemin örneklerini ve çözülmüş alıştırmalarını da görebilirsiniz.

$\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)$

$\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}$

$\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}$

Öte yandan doğrunun vektörünün büyüklüğünü buluyoruz

$r:$

$\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}$

Son olarak her terimin değerini formülde yerine koyarız ve çizgiler arasındaki mesafeyi hesaplarız:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}$

Dolayısıyla iki hat arası mesafe 3,60 birimdir.

Uzayda kesişen iki çizgi arasındaki mesafe nasıl belirlenir

Başlangıçta gördüğümüz gibi, kesişen iki çizgi arasındaki mesafeyi belirleme yöntemi, paralel çizgiler arasındaki mesafeleri belirleme yönteminden farklıdır.

uzayda çapraz çizgiler arasındaki mesafe

Bu nedenle uzayda kesişen iki çizgi arasındaki mesafeyi belirlemek için çeşitli yöntemler vardır. Bu sayfada yalnızca en basit olan bir prosedürü açıklayacağız, çünkü diğer iki yöntem daha uzun ve daha karmaşıktır, aslında pratikte kullanılmazlar.

Yön vektörü ve kesişen iki çizginin herhangi bir noktası şöyle olsun:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

Kesişen iki çizgi arasındaki mesafenin formülü :

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Altın

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

vektörlerin karışık çarpımının mutlak değeridir

$\vv{\text{u}}, \vv{\text{v}}$

ve noktalarla tanımlanan vektör

$A$

$B$

. Öte yandan,

$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

çapraz iki çizginin yön vektörleri arasındaki çapraz çarpımın genliğidir.

Çapraz iki çizgi arasındaki mesafenin nasıl belirleneceğini görebilmeniz için örnek olarak bir problem çözeceğiz:

Sonraki iki kesişen çizgi arasındaki mesafe nedir?

$r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}$

$s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}$

Öncelikle yön vektörünü ve her doğru üzerinde bir noktayı tanımlamamız gerekiyor. Bu nedenle iki çizgi sürekli bir denklem biçiminde ifade edilir:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}$

Şimdi kesişen iki çizgi arasındaki mesafenin formülünü uyguluyoruz:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

Bir yandan karışık çarpımı (veya üçlü skaler çarpımı) çözüyoruz:

$\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)$

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13$

Ve diğer taraftan çapraz çarpımın (veya çapraz çarpımın) modülünü buluyoruz:

$\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}$

$\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}$

Son olarak, formüldeki her bir terimin değerini, çapraz iki çizgi arasındaki mesafenin yerine koyarız:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}$

Uzayda iki çizgi arasındaki mesafe (r3'te)

İki çizgi arasındaki mesafe nasıl hesaplanır

Uzayda iki paralel çizgi arasındaki mesafe nasıl bulunur?

Uzayda kesişen iki çizgi arasındaki mesafe nasıl belirlenir

Yorum bırakın Yanıtı iptal et