İki çizgi arasındaki kesişme veya kesişme noktasını hesaplayın

Burada iki çizgi arasındaki kesme noktasının (veya kesişiminin) nasıl hesaplandığını bulacaksınız. Ayrıca örnekleri göreceksiniz ve adım adım çözülen alıştırmalarla pratik yapabilirsiniz.

İki çizgi arasındaki kesme veya kesişme noktası nedir?

İki çizgi arasındaki kesişme (veya kesim) noktası, iki farklı çizginin kesiştiği noktadır. Dolayısıyla iki farklı doğrunun kesişimi veya kesme noktası olması, onların bir noktada çakıştığı anlamına gelir.

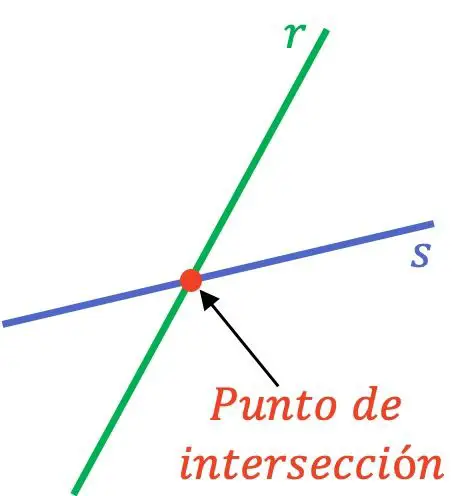
İki doğrunun bir noktada kesişmesi için bunların kesişen doğrular olması gerekir çünkü paralel doğrular hiçbir noktada birbirine değmez.

Şu anda kesişen çizgilerin tam olarak ne olduğunu hatırlamıyorsanız, bu tür çizgilerin ne olduğu ve iki çizginin kesişip kesişmediğini nasıl anlayacağınız hakkında ayrıntılı bir açıklama bulacağınız Kesişen Çizgi Örnekleri sayfamıza göz atmanızı öneririz.

İki çizgi arasındaki kesme veya kesişme noktası nasıl hesaplanır?

İki doğrunun kesiştiği veya kesiştiği noktanın tanımını gördükten sonra şimdi söz konusu noktanın nasıl hesaplandığına bakalım.

İki çizginin kesişme noktasını (veya kesişim noktasını) bulmak için öncelikle iki çizginin paralel olmadığından emin olmalısınız, çünkü bunlar iki paralel çizgiyse hiçbir noktada kesişmezler. Bu nedenle, öncelikle iki doğrunun ne zaman paralel olup ne zaman olmadığını nasıl belirleyeceğinizi bilmeniz gerekir; Nasıl yapılacağını hatırlamıyorsanız linke tıklayarak tekrar izleyebilirsiniz.

İki doğrunun paralel olmadığını bildiğimizde, iki doğru arasındaki kesişme (veya kesişme) noktasını belirlemek için her doğrunun denkleminden oluşan denklem sistemini çözmeliyiz. Ve söz konusu denklem sisteminin sonucu, iki çizgi arasındaki kesişme (veya kesişme) noktasının koordinatları olacaktır.

İki çizgi arasındaki kesişme veya kesişme noktasının nasıl bulunacağına ilişkin örnek

Örnek olarak, 2 doğrunun kesişme noktasını (veya kesişim noktasını) nasıl bulacağınızı görebilmeniz için bir problem çözeceğiz:

Aşağıdaki iki doğrunun kesişme noktasını bulun:

$r: \ y=4x-1 \qquad \qquad s: \ y=-2x+5$

Birincisi, doğrular paralel değildir çünkü eğimleri farklıdır, dolayısıyla her ikisi de Kartezyen düzlemde bir noktada kesişir.

Bunu bulmak için her doğrunun denkleminden oluşan denklem sistemini çözmeliyiz:

$\left. \begin{array}{l} y=4x-1 \\[2ex] y=-2x+5 \end{array} \right\}$

Bu özel durumda, iki bilinmeyen olduğundan sistemi eşitleme yöntemiyle çözeceğiz.

$y$

zaten çözüldü (her iki satır da açık denklem formundadır):

$y= y$

$4x-1=-2x+5$

Değişkenin değerini siliyoruz

$x:$

$4x+2x=5+1$

$6x=6$

$x = \cfrac{6}{6}$

$x = 1$

Ve ne kadar değerli olduğunu öğrendiğinde

$x,$

Değerini bulmak için değerini herhangi bir denklemde yerine koyarız.

$y:$

$y=4x-1 \ \xrightarrow{x \ = \ 1} \ y=4\cdot 1-1$

$y =4-1$

$y =3$

Böylece iki doğrunun kesiştiği noktanın koordinatları şöyle olur:

$\bm{(1,3)}$

İki çizginin kesişme veya kesişme noktası sorunları çözüldü

1. Egzersiz

Aşağıdaki iki doğrunun kesişme veya kesişme noktası nedir?

$r: \ y=x+5 \qquad \qquad s: \ y=2x+3$

Çözüme bakın

Birincisi, çizgiler paralel değildir çünkü eğimleri farklıdır, dolayısıyla iki çizgi düzlemin bir noktasında buluşacaktır.

Söz konusu noktayı hesaplamak için her doğrunun denkleminden oluşan denklem sistemini çözmek gerekir:

$\left. \begin{array}{l} y=x+5 \\[2ex] y=2x+3 \end{array} \right\}$

Bu durumda iki bilinmeyen olduğundan denklem sistemini eşitleme yöntemiyle çözeceğiz.

$y$

zaten çözüldü (her iki satır da açık denklem formundadır):

$y= y$

$x+5=2x+3$

Değişkenin değerini siliyoruz

$x:$

$x-2x=3-5$

$-x=-2$

$x=2$

Ve ne kadar değerli olduğunu öğrendiğinde

$x,$

Değerini bulmak için değerini herhangi bir denklemde yerine koyarız.

$y:$

$y=x+5 \ \xrightarrow{x \ = \ 2} \ y=2+5$

$y =7$

Dolayısıyla iki çizgi arasındaki kesişme noktasının koordinatları şöyledir:

$\bm{(2,7)}$

Alıştırma 2

Aşağıdaki iki çizginin kesişme veya kesişme noktasını bulun:

$r: \ y=-3x+1 \qquad \qquad s: \ 4x+2y+6=0$

Çözüme bakın

doğru

$s$

Örtülü (veya genel) bir denklem biçiminde ifade edilir, dolayısıyla eğiminin değerini bilmek için önce onu açık bir denklem biçiminde aktaracağız:

$4x+2y+6=0$

$2y=-4x-6$

$y=\cfrac{-4x-6}{2}$

$y=-2x-3$

Yani iki doğrunun eğimleri farklıdır ve dolayısıyla aralarında bir kesişme noktası vardır.

Söz konusu noktayı hesaplamak için her doğrunun denkleminden oluşan denklem sistemini çözmek gerekir:

$\left. \begin{array}{l} y=-3x+1\\[2ex] y=-2x-3 \end{array} \right\}$

Denklem sistemini eşitleme yöntemiyle çözüyoruz:

$y= y$

$-3x+1=-2x-3$

Değişkenin değerini siliyoruz

$x:$

$-3x+2x=-3-1$

$-x=-4$

$x=4$

Ve ne kadar değerli olduğunu öğrendiğinde

$x,$

Değerini bulmak için değerini her iki denklemde yerine koyarız.

$y:$

$y=-3x+1 \ \xrightarrow{x \ = \ 4} \ y=-3\cdot 4+1$

$y =-12+1$

$y =-11$

Dolayısıyla iki çizgi arasındaki kesişme noktasının koordinatları şöyledir:

$\bm{(4,-11)}$

Alıştırma 3

Aşağıdaki iki çizgi arasındaki kesişme noktasını veya kesişim noktasını belirleyin:

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

Çözüme bakın

Öncelikle bunların iki paralel doğru olup olmadığını bilmemiz gerekiyor. Bunu yapmak için iki doğrunun yön vektörlerinin orantılı olup olmadığına bakacağız.

doğru

$r$

parametrik denklemler biçiminde tanımlanır, dolayısıyla yön vektörünün bileşenleri parametrenin önündeki katsayılardır

$t:$

$\vv{r} =(2,-3)$

Ve diğer taraftan çizgi

$s$

örtülü bir denklem biçiminde tanımlanır, dolayısıyla yön vektörü şöyledir:

$\vv{s} =(-B,A)=(-2,4)$

İki yön vektörünün bileşenleri birbiriyle orantılı olmadığından iki doğru paralel değildir.

$\cfrac{2}{-2} \neq \cfrac{-3}{4} \ \longrightarrow \ r \ \cancel{\parallel} \ s$

Ve iki doğru paralel olmadığı için bu, aralarında gerçekten bir kesişme noktasının olduğu anlamına gelir. Bunu hesaplamak için her satırın denkleminden oluşan denklem sistemini çözmeliyiz:

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

Bu durumda çizgi gibi

$r$

parametrik denklemler şeklinde olduğundan, her bir parametrik denklemin ifadesini diğer satırın denklemine koymak gerekir:

$4(1+2t)+2(-2-3t)+8=0$