Dik düzlemler

Bu sayfada dik düzlemlerin ne olduğunu, iki düzlemin dik olup olmadığının nasıl belirleneceğini, dik düzlemin nasıl hesaplanacağını, dik düzlemlerle ilgili örnekleri ve çözülmüş alıştırmaları bulacaksınız…

İki dik düzlem nedir?

Analitik geometride, iki düzlem dik açıyla (90°) kesiştiğinde diktir.

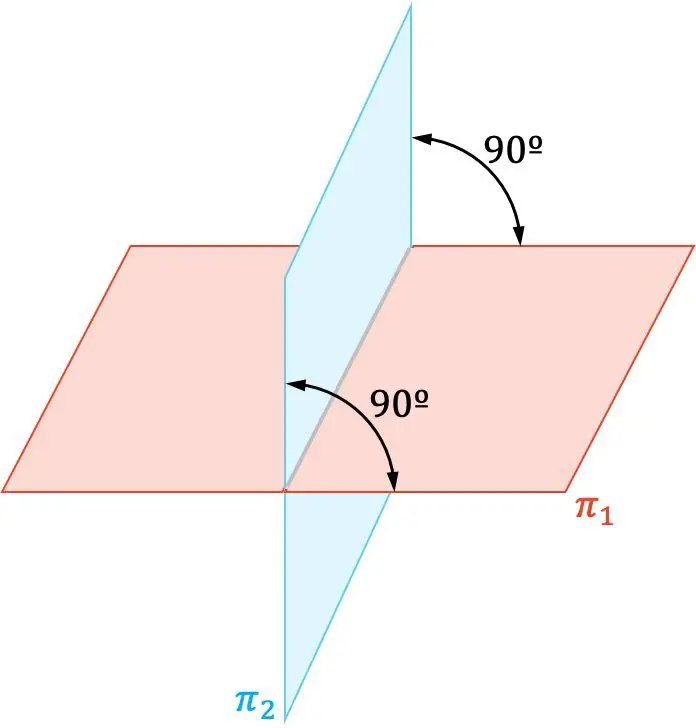
Ayrıca iki dik düzlemin normal vektörleri de birbirine diktir.

Açıkçası, iki dik düzlem arasındaki mesafe her zaman sıfırdır çünkü bunlar bir doğru üzerinde kesişir. Her ne kadar çok basit gibi görünse de iki uçak arasındaki mesafe kavramı oldukça önemli olduğundan bu konuda sorularınız varsa bağlantıyı ziyaret etmenizi öneririz.

Öte yandan, dikey olarak konumlandırılmış iki düzlem, düzlemler arasında mümkün olan tek göreceli konum değildir, çünkü uzaydaki (R3’te) iki düzlem de kesişebilir, paralel veya çakışık olabilir.

Bir düzlemin diğerine dik olup olmadığını nasıl anlarsınız?

Dik düzlemlerin tanımını gördükten sonra, iki düzlemin dik olup olmadığını nasıl anlayacağımıza bakalım:

Normal vektörleri dik olduğunda iki düzlem diktir. Bu nedenle iki düzlemin birbirine dik olup olmadığını belirlemek için normal vektörlerinin oluşturduğu açıyı hesaplamamız gerekir, eğer bunlar 90 derecelik bir açı oluşturuyorsa bu, düzlemlerin dik olduğu anlamına gelir.

Yani iki düzlemin dikliğini bulmak için iki vektör arasındaki açının nasıl hesaplanacağını bilmeniz gerekir. Nasıl yapılacağını hatırlamıyorsanız, açıklamamızı ve iki vektör arasındaki açıyı belirlemek için gerekli formülü bulabileceğiniz bağlantıya başvurabilirsiniz. Ayrıca örnekleri görebilecek ve çözümlü alıştırmalarla pratik yapabileceksiniz.

Ancak kısacası, iki vektörün iç çarpımları sıfır olduğunda birbirine diktir. Bu nedenle, ilişkili normal vektörlerinin nokta çarpımı 0 olduğunda iki düzlem birbirine dik olacaktır.

İki dik düzlem örneği

Örneğin aşağıdaki iki düzlemin dik olup olmadığını kontrol edelim:

Bir düzleme normal olan vektörün X, Y, Z koordinatları, genel (veya örtülü) denkleminin A, B, C katsayılarıyla çakışır. Bu nedenle, her düzlemin normal vektörü şöyledir:

Şimdi normal vektörleri arasındaki nokta çarpımı hesaplayarak bunların iki dik düzlem olup olmadığını kontrol ediyoruz:

İki normal vektör arasındaki nokta çarpım 0’dır, dolayısıyla iki düzlem birbirine diktir .

Bir noktada bir çizgiye dik olan bir düzlemi hesaplayın

Tipik bir düzlem ve doğru problemi, belirli bir noktada bir çizgiye dik olan bir düzlemin denklemini bulmaktır. Şimdi bir örnekle bunun nasıl çözüldüğünü göreceğiz:

• Doğruya dik olan düzlemin denklemini bulunuz.

  

  Hakkında

  

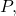
  doğrudan söylenerek ve vurgulanarak:

Öncelikle söz konusu düzleme dik vektörü bulmamız gerekiyor. ve düz bir çizgi gibi

düzleme dik ise normal vektörü doğrunun yön vektörüyle çakışacaktır.

Bu durumda satır

parametrik denklemler biçimindedir, dolayısıyla yön vektörünün bileşenleri parametrenin önündeki terimlerdir

Böylece düzleme dik vektör, doğrunun yön vektörüyle aynı olacaktır:

Ve dolayısıyla planın örtülü (veya genel) denklemi şu şekilde olacaktır:

Bu nedenle D katsayısının değerini belirlemek yeterlidir. Bunu yapmak için, ifadesinde düzleme ait olduğunu söyleyen noktanın koordinatlarını denkleminde yerine koyarız:

Kısaca düzlemin Kartezyen denklemi şöyledir:

Öte yandan geometrik cisimler arasındaki diklik konusunda daha fazla alıştırma yapmak isterseniz dik doğrular sayfamızı ziyaret edebilirsiniz. Dik çizgiler hakkında bilmeniz gereken her şeyi bulacaksınız: iki doğru dik olduğunda, bir çizginin diğerine dik olarak nasıl hesaplanacağı, örnekler, çözümlü alıştırmalar ve çok daha fazlası.

Dik düzlemlerin özellikleri

Tüm dikey düzlemler aşağıdaki özelliklere sahiptir:

• Simetrik ilişki : Bir düzlem başka bir düzleme dik ise bu düzlem de birinci düzleme diktir. Bu özellik aynı zamanda paralel düzlemler tarafından da tutulur.

• Yansımama özelliği : Açıkçası hiçbir düzlem kendisine dik olamaz.

• Teorem: Üç boyutlu (3 boyutlu) uzayda, üçüncü bir düzleme dik olan herhangi bir düzlem çifti mutlaka paralel olmalıdır. Yani bir düzlem başka bir düzleme dik ise ve bu düzlem üçüncü bir düzleme de dik ise birinci ve son düzlemler birbirine paraleldir.