Paralel düzlemler

Bu sayfada paralel düzlemler hakkında her şeyi bulacaksınız: iki düzlem paralel olduğunda, iki paralel düzlemin denklemleri, örnekler, çözülmüş alıştırmalar, özellikler,…

İki paralel düzlem nedir?

Analitik geometride, birbirlerinden her zaman aynı uzaklıkta olan iki düzlem paraleldir. Bu nedenle iki paralel düzlem asla kesişmez ve hiçbir ortak yanı yoktur.

Paralel konumlandırılmış iki düzlem, düzlemler arasındaki tek mümkün göreceli konum değildir, çünkü uzaydaki (R3’te) iki düzlem de kesişebilir veya çakışabilir.

İki düzlemin paralel olup olmadığını nasıl anlarsınız?

Paralel düzlemlerin tanımını gördükten sonra iki düzlemin paralel olup olmadığını nasıl belirleyeceğinizi görelim.

İki farklı planın genel (veya örtülü) denkleminden yola çıkarak:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

A, B ve C katsayıları D katsayısı ile değil de birbirleriyle orantılı ise 2 düzlem paralel olacaktır. Başka bir deyişle, iki düzlem arasındaki paralellik aşağıdaki denklem yerine getirildiğinde ortaya çıkar:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

İki paralel düzlem örneği

Örneğin aşağıdaki iki düzlem paraleldir:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

Planlar paraleldir çünkü X, Y, Z değişkenlerinin katsayıları birbirleriyle orantılıdır ancak bağımsız terimlerle orantılı değildir:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

İki paralel düzlem arasındaki mesafeyi hesaplayın

İki paralel düzlem her zaman aynı uzaklıkta olduğundan, iki paralel düzlem arasındaki mesafeyi bulmak için iki düzlemden birinde bir nokta alıp o noktanın diğer düzleme olan mesafesini hesaplayabiliriz. Bu nedenle 2 paralel düzlem arasındaki mesafeyi hesaplamak için bir noktadan bir düzleme olan mesafenin formülünü bilmek gerekir.

İki paralel düzlem arasındaki mesafeyi bulmak için kullanılan bir yöntemdir. Ancak iki düzlemin denklemlerinin A, B ve C katsayıları çakıştığında bunu yapmanın daha da basit bir yolu vardır:

İki paralel düzlemin genel (veya örtülü) denklemlerini düşünün:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

İki paralel düzlem arasındaki mesafeyi hesaplamak için formül :

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

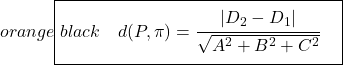
Dolayısıyla iki paralel düzlem arasındaki mesafeyi formülü kullanarak bulmak kesinlikle daha kolaydır, çünkü bu sadece formülü uygulama meselesidir ve bu kadardır, ancak soruna bağlıdır. Ek olarak, tercih ettiğiniz yöntemi seçebilmeniz için mesafeyi hesaplamanın her iki yolunu da açıklamanın en iyisi olacağını düşünüyoruz.

İki paralel düzlem arasındaki mesafeyi hesaplama örneği

Örnek olarak aşağıdaki iki düzlem arasındaki mesafeyi hesaplayacağız:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Öncelikle iki paralel düzlemle karşı karşıya olduğumuzu doğrulamalıyız. Dolayısıyla, düzlem denklemlerinin tüm katsayıları bağımsız terimler dışında orantılıdır, dolayısıyla bunlar fiilen iki paralel düzlemdir.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Bu durumda iki düzlemin denklemlerinin A, B ve C terimleri çakışmamaktadır ancak bunu ikinci düzlemin denkleminin tamamını ikiye bölerek başarabiliriz:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Yani iki düzlemin denklemleri artık aynı A, B ve C katsayılarına sahip. Dolayısıyla iki paralel düzlem arasındaki uzaklık formülüyle iki düzlem arasındaki uzaklığı kolaylıkla hesaplayabiliriz:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Değerleri değiştiriyoruz ve işlemleri çözüyoruz:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Böylece bir düzlem ile diğer düzlem arasındaki mesafe birliğe eşit olur.