Bu sayfada uzaydaki bir nokta ile düzlem arasındaki mesafenin nasıl hesaplandığını (formül) bulacaksınız. Ayrıca örnekleri görebilecek ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz.
Bir noktanın bir düzleme olan uzaklığı nedir?
Analitik geometride, bir noktadan bir düzleme olan uzaklık, o nokta ile düzlem üzerindeki herhangi bir nokta arasındaki en kısa uzaklıktır. Bu mesafe, noktadan düzleme giden düzleme dik olan doğru parçasının uzunluğuna karşılık gelir.

Bir noktadan düzleme olan mesafenin formülü
Bir nokta ile düzlem arasındaki mesafe kavramını tam olarak gördükten sonra, şimdi söz konusu mesafeyi hesaplamak için kullanılan formüle bakalım:
Bir nokta ve bir düzlemin genel (veya örtülü) denklemi verildiğinde:
![]()
Bir noktadan düzleme olan mesafenin formülü :
![]()
Bir noktadan düzleme olan uzaklığın formülünün ispatı oldukça sıkıcı ve uzun olduğundan bu sayfada yapmayacağız.
Öte yandan, formülü uygularken sıfıra eşit bir sonuç elde edersek, bu açıkça nokta ile düzlem arasındaki mesafenin sıfır olduğu ve dolayısıyla noktanın o düzlemin parçası olduğu anlamına gelir.
Son olarak, formülü uygulamak için planın genel (veya örtülü) bir denklem olarak tanımlanması gerektiğini unutmayın. Yani başka türde bir düzlem denklemiyle ifade edilseydi, önce onu genel bir denkleme dönüştürmemiz, sonra formülü kullanmamız gerekirdi.
Bir noktadan düzleme olan mesafeyi hesaplama örneği
Bir nokta ile düzlem arasındaki mesafenin sayısal olarak nasıl belirlendiğini görebilmeniz için aşağıdaki örneği çözeceğiz:
- P noktası ile π düzlemi arasındaki mesafeyi hesaplayın. Nokta ve planı söyledikten sonra:
![]()
Noktadan düzleme olan mesafeyi bulmak için yukarıdaki bölümde görülen formülü uygulamanız yeterlidir:
![]()
Şimdi her bilinmeyenin değerini formülde yerine koyuyoruz:
![]()
Ve son olarak işlemleri gerçekleştiriyoruz:
![]()
![]()
Kesirin payının mutlak bir değer olduğunu ve paydanın da karekökü olduğunu, dolayısıyla sonucun her zaman pozitif olması gerektiğini unutmayın. Bu mantıklı çünkü mesafeler negatif olamaz, ancak her zaman pozitiftir.
İki paralel düzlem arasındaki mesafeyi hesaplayın
İki paralel düzlem her zaman aynı uzaklıkta olduğundan, iki paralel düzlem arasındaki mesafeyi bulmak için iki düzlemden birinde bir nokta alıp o noktanın diğer düzleme olan mesafesini hesaplayabiliriz.

İki paralel düzlem arasındaki mesafeyi bulmak için kullanılan bir yöntemdir. Ancak iki düzlemin denklemlerinin A, B ve C katsayıları çakıştığında bunu yapmanın daha da basit bir yolu vardır:
İki paralel düzlemin genel (veya örtülü) denklemlerini düşünün:
![]()
İki paralel düzlem arasındaki mesafeyi hesaplamak için formül :
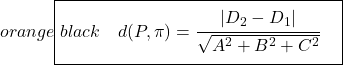
Dolayısıyla iki paralel düzlem arasındaki mesafeyi formülü kullanarak bulmak kesinlikle daha kolaydır, çünkü bu sadece formülü uygulama meselesidir ve bu kadardır, ancak soruna bağlıdır. Ek olarak, tercih ettiğiniz yöntemi seçebilmeniz için mesafeyi hesaplamanın her iki yolunu da açıklamanın en iyisi olacağını düşünüyoruz.
İki paralel düzlem arasındaki mesafeyi hesaplama örneği
Örnek olarak aşağıdaki iki düzlem arasındaki mesafeyi hesaplayacağız:
![]()
Öncelikle iki paralel düzlemle karşı karşıya olduğumuzu doğrulamalıyız. Dolayısıyla, düzlem denklemlerinin tüm katsayıları bağımsız terimler dışında orantılıdır, dolayısıyla bunlar fiilen iki paralel düzlemdir.
![]()
Bu durumda iki düzlemin denklemlerinin A, B ve C terimleri çakışmamaktadır ancak bunu ikinci düzlemin denkleminin tamamını ikiye bölerek başarabiliriz:
![]()
![]()
Yani iki düzlemin denklemleri zaten aynı A, B ve C katsayılarına sahiptir. Dolayısıyla iki paralel düzlem arasındaki mesafe formülüyle iki düzlem arasındaki mesafeyi kolayca hesaplayabiliriz:
![]()
Değerleri değiştiriyoruz ve işlemleri çözüyoruz:
![]()
Böylece bir düzlem ile diğer düzlem arasındaki mesafe birliğe eşit olur.
Bir noktadan düzleme olan mesafe problemlerini çözme
1. Egzersiz
P noktası ile Kartezyen (veya genel) denklemi şu olan düzlem arasındaki mesafeyi hesaplayın:
![]()
Noktadan düzleme olan mesafeyi hesaplamak için ilgili formülü kullanmanız gerekir:
![]()
Her parametrenin değerini formülde değiştiririz:
![]()
Ve son olarak işlemleri gerçekleştiriyoruz:
![]()
![]()
![]()
Alıştırma 2
P noktası ile π düzlemi arasındaki mesafeyi bulun:
![]()
Bir noktadan bir düzleme olan uzaklık formülünü kullanmadan önce, öncelikle düzlemi örtülü (veya genel) bir denklem biçiminde ifade etmeliyiz:
![]()
Artık noktadan düzleme olan mesafeyi belirlemek için formülü kullanabiliriz:
![]()
Her terimin değerini formülde değiştiririz:
![]()
Ve son olarak işlemleri gerçekleştiriyoruz:
![]()
![]()
Alıştırma 3
P noktasının π düzleminde olup olmadığını belirlemek için bir nokta ile düzlem arasındaki mesafe formülünü kullanın.
![]()
Noktanın düzleme ait olup olmadığını kontrol etmek için ikisi arasındaki mesafeyi hesaplayabiliriz: mesafe sıfırsa bu noktanın düzleme ait olduğu anlamına gelir, öte yandan mesafe 0’dan farklıysa bu da noktanın düzleme ait olduğu anlamına gelir. nokta düzlemin dışındadır. plan.
Bu nedenle nokta ile düzlem arasındaki mesafeyi formülden belirleriz:
![]()
![]()
![]()
![]()
![]()
Nokta ile düzlem arasındaki mesafe sıfıra eşdeğerdir, dolayısıyla nokta düzleme aittir.
Alıştırma 4
Aşağıdaki iki düzlem arasındaki mesafeyi bulun:
![]()
Öncelikle iki paralel düzlemle karşı karşıya olduğumuzu doğrulamalıyız. İki düzlemin denklemlerinin tüm katsayıları bağımsız terimler dışında orantılıdır, yani bunlar aslında iki paralel düzlemdir.
![]()
Bu durumda A, B ve C katsayıları eşit olduğundan iki düzlem arasındaki mesafeyi formülle hesaplayacağız:
![]()
Böylece değerleri formülde yerine koyuyoruz ve işlemleri gerçekleştiriyoruz:
![]()
Alıştırma 5
Aşağıdaki iki paralel düzlem arasındaki mesafeyi bulun:
![Rendered by QuickLaTeX.com \pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d14719b0eefd313552d5257c249c66f_l3.png)
Ön plan düzlemi parametrik denklemler biçiminde tanımlanır, dolayısıyla iki paralel düzlem arasındaki mesafe formülünü uygulamak için önce onu genel bir denklem biçimine dönüştürmemiz gerekir ve bu, çok fazla hesaplama ve zaman gerektirir. Dolayısıyla o düzlem üzerinde bir nokta alıp o noktadan diğer düzleme olan mesafeyi hesaplarsak daha hızlı olur.
Böylece, π 1 düzleminin geçtiği bir noktanın koordinatları, her parametrik denklemin bağımsız terimlerine karşılık gelir:
![]()
Şimdi bu nokta ile diğer düzlem arasındaki mesafeyi bulmak için formülü uyguluyoruz:
![]()
![]()
![]()
![]()
![]()
Bu nedenle iki paralel düzlem arasındaki mesafe:
![]()