▷ Bir fonksiyonun eğik asimptotu (çözülmüş alıştırmalar)

Bu makalede bir fonksiyonun eğik asimptotlarının ne olduğunu açıklayacağız. Bir fonksiyonun ne zaman eğik asimptotu olduğunu ve bunun nasıl hesaplandığını öğreneceksiniz. Ayrıca eğik asimptot örneklerini görebilecek ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Eğik asimptot nedir?

Bir fonksiyonun eğik asimptotu, grafiğinin onu hiç kesmeden sonsuza kadar yaklaştığı eğik bir çizgidir. Sonuç olarak, tüm eğik asimptotlar y=mx+n denklemine sahip doğrulardır.

Eğik bir asimptotun eğimi ve kökeni aşağıdaki formüller kullanılarak hesaplanır:

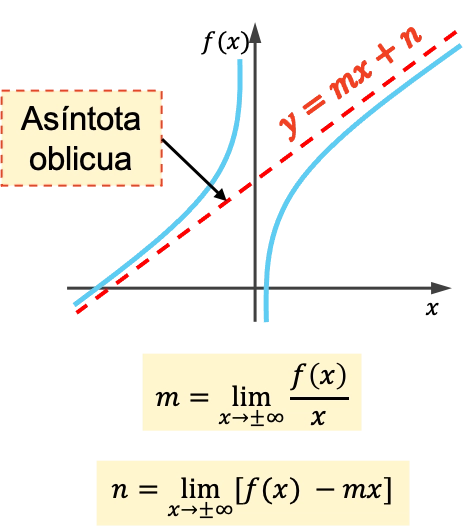
Bir fonksiyonun eğik asimptotu nasıl hesaplanır

Bir fonksiyonun eğik asimptotunu hesaplamak için aşağıdaki adımlar gerçekleştirilmelidir:

Fonksiyonun sonsuz limitini x’e bölerek hesaplayın.
Yukarıdaki limit sıfırdan farklı bir gerçek sayıyla sonuçlanıyorsa, bu, fonksiyonun eğik bir asimptotu olduğu anlamına gelir. Üstelik söz konusu eğik asimptotun eğimi, sınırda elde edilen değer olacaktır.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

Bu durumda geriye kalan tek şey, aşağıdaki limiti çözerek eğik asimptotun kesim noktasını hesaplamaktır:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Not: Limitlerin artı ve eksi sonsuzda hesaplanması gerekir, ancak normalde aynı sonucu verirler ve bu nedenle ±∞ koyarak basitleştirme yapıyoruz. Ancak artı ve eksi sonsuzdaki sınırlar farklı olsaydı sol eğik asimptot ve sağ eğik asimptotun ayrı ayrı hesaplanması gerekirdi.

Eğik Asimptot Örneği

Daha sonra, aşağıdaki rasyonel fonksiyonun eğik asimptotunu alacağız, böylece bunun nasıl yapıldığına dair bir örnek görebilirsiniz:

$f(x)=\cfrac{x^2+1}{x}$

Eğik asimptotlar şu türdendir:

$y=mx+n.$

İlk önce doğrunun eğimini hesaplıyoruz

$m$

karşılık gelen formülüyle:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

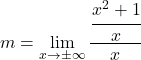
Bu sınırı çözmek için kesirlerin özelliklerini uygulamalıyız:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

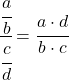
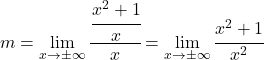
Şimdi limiti hesaplıyoruz:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

Bu durumda sonsuzun sonsuzluk arasındaki belirsizliğinin sonucu, pay ve payda aynı mertebeden olduğundan x’in en yüksek derecedeki katsayılarının bölünmesidir.

Yukarıdaki limit sıfırdan farklı bir gerçek sayı verir, dolayısıyla fonksiyonun eğik bir asimptotu vardır. Şimdi y kesme noktasını hesaplayacağız

$n$

karşılık gelen formülü kullanarak asimptotun değeri:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

Limiti hesaplamaya çalışıyoruz:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Ama belirsizlik sonsuz eksi sonsuz elde ederiz. Bu nedenle terimleri ortak bir paydaya indirgemek gerekir. Bunu yapmak için x’i kesrin paydasıyla çarpıp bölüyoruz:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Artık iki terim aynı paydaya sahip olduğuna göre bunları gruplandırabiliriz:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

Pay üzerinde çalışıyoruz:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

Ve son olarak limiti çözüyoruz:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

Yani n =0. Bu nedenle eğik asimptot doğrusal bir fonksiyondur:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

İncelenen fonksiyon aşağıdaki grafikte gösterilmektedir. Gördüğünüz gibi fonksiyon y=x doğrusuna çok yaklaşıyor ancak eğik bir asimptot olduğu için ona asla dokunmuyor:

Eğik asimptotlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki rasyonel fonksiyonun eğik asimptotunu bulun:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Çözümü görün

Eğik asimptotlar şu şekildedir:

$y=mx+n$

bu nedenle m ve n parametrelerinin hesaplanması gereklidir. İlk önce m’yi formülünü uygulayarak hesaplıyoruz:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

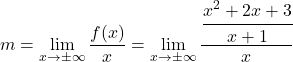
Kesirlerin özelliklerini uygulayarak kesri basitleştiririz:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

Ve limiti çözüyoruz:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Yani m =1. Şimdi eğik asimptotun kesim noktasını formülünü uygulayarak hesaplayalım:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

Limiti hesaplamaya çalışıyoruz:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Ama sonsuz eksi sonsuzun belirsiz formunu elde ederiz. Bu nedenle terimleri ortak bir paydaya indirgemeli ve sonra bunları gruplandırmalıyız:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

Ve son olarak limiti çözüyoruz:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

Kısaca fonksiyonun eğik asimptotu şöyledir:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Alıştırma 2

Aşağıdaki rasyonel fonksiyonun tüm eğik asimptotlarını bulun:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Çözümü görün

İlk olarak eğik asimptotun eğimi için formülü kullanıyoruz:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

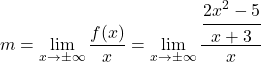
Kesirlerin özelliklerini uygulayarak kesri basitleştiririz:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

Ve sınırı belirliyoruz:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

Limit sıfırdan farklı bir gerçek sayı verir, dolayısıyla eğimi 2 olan eğik asimptotu olan rasyonel bir fonksiyondur.

Şimdi ilgili formülü uygulayarak kesişmeyi hesaplayalım:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

Limiti hesaplamaya çalışıyoruz:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Ama sonsuzlukların fark belirsizliğini elde ederiz. Bu nedenle terimleri ortak bir paydaya indiririz ve ardından şunu çalıştırırız:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

Ve son olarak limiti çözüyoruz:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

Özetle, kesirli fonksiyonun eğik asimptotu şöyledir:

$y = mx+n$

$\bm{y=2x-6}$

Eğik asimptot nedir?

Bir fonksiyonun eğik asimptotu nasıl hesaplanır

Eğik Asimptot Örneği

Eğik asimptotlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Yorum bırakın Yanıtı iptal et