Başka bir noktaya, bir doğruya ve bir düzleme göre simetrik olan nokta

Burada başka bir noktaya göre, bir doğruya ve bir düzleme göre simetri noktasının nasıl hesaplanacağını bulacaksınız. Ayrıca adım adım çözülen örnekleri ve alıştırmaları görebileceksiniz.

Başka bir noktaya simetrik nokta

Simetrik noktanın nasıl hesaplandığına bakmadan önce, başka bir noktaya göre simetrik noktanın tam olarak ne olduğuna bakalım:

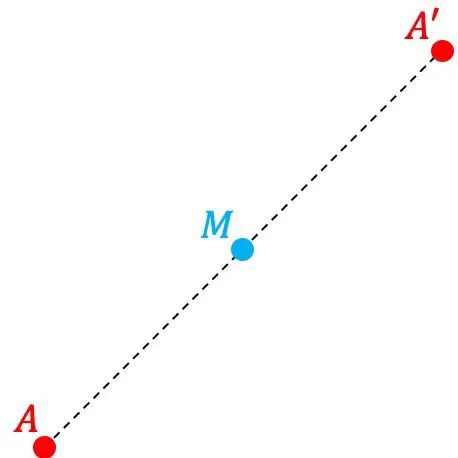
A’ noktası, M noktasından A ve M noktaları arasındaki mesafeyle aynı uzaklıkta simetrik olarak bulunuyorsa, A’ noktası A noktasının başka bir M noktasına göre simetrik noktasıdır. Bu nedenle M, aşağıdakilerle oluşturulan parçanın orta noktasıdır: A ve A’ noktaları.

$d(A,M) = d(A',M )$

Öte yandan M noktasının da simetri merkezi olduğunu söylüyoruz.

Dolayısıyla simetri noktasının koordinatlarını hesaplamak için parçanın orta noktası formülünü kullanacağız:

$\cfrac{A+A'}{2}=M$

Bu denklemden bilinmeyen A’ noktasını çıkarırız ve başka bir noktaya göre simetrik olan noktanın formülünü elde ederiz:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

Başka bir noktaya göre simetrik noktayı bulma örneği

Örnek olarak A noktasının M noktasına göre simetri noktasını hesaplayacağız. İki noktayı düşünün:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

Bu iki nokta arasındaki simetri noktasını belirlemek için diğerine göre simetri noktası formülünü uygularız:

$A' = 2M - A$

Şimdi formüldeki noktaları değiştiriyoruz:

$A' = 2(-1,4,2) -(1,3,0)$

Ve biz çalışıyoruz:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

bir doğruya simetrik olan nokta

Az önce başka bir noktaya göre simetrik olan bir nokta kavramını gördük. Bir noktanın bir çizgiye göre simetrik noktası çok benzer:

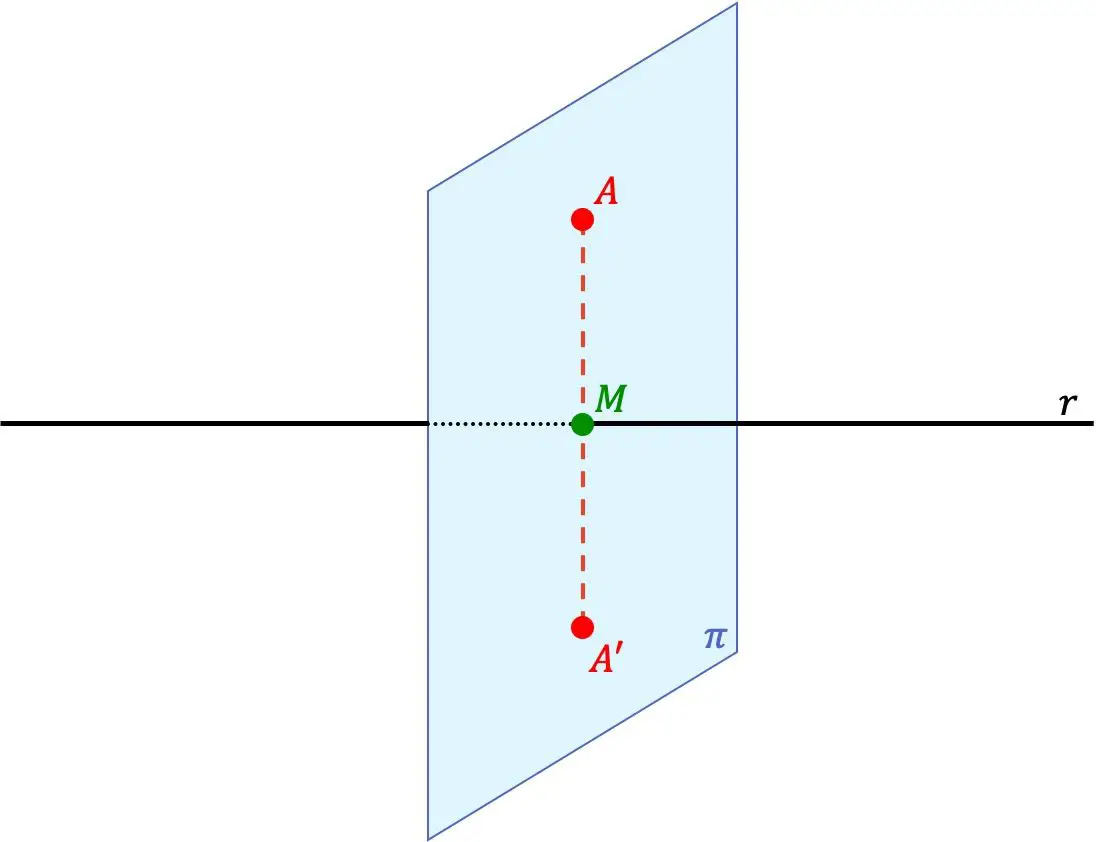
A’ noktası, iki A’ ve A noktası çizgiye dik olarak aynı çizgi üzerinde yer alıyorsa ve ayrıca A’ noktası ile çizgi arasındaki mesafe mesafeye eşitse, A noktasının bir çizgiye göre simetrik noktasıdır. A noktası ile doğru arasında.

bir noktanın bir doğruya göre simetrik noktası

$d(A,r)= d(A',r)$

Yani r doğrusu aynı zamanda noktalar arasındaki simetri eksenidir.

Bu nedenle, A noktasının r doğrusuna göre simetri noktasını belirlemek için aşağıdaki prosedürü izlemeliyiz:

A noktasından geçen r çizgisine dik olan düzlemi buluyoruz (önceki grafik gösterimin π düzlemi). Bunu yapmak için düzlemin normal vektörü olacak doğrunun yön vektörünü kullanmalıyız.
Bulunan düzlem ile çizgi arasındaki kesişme noktasını hesaplıyoruz (önceki görüntüdeki M noktası).
A noktasının M noktasına göre simetrik noktasını bulmak için (yukarıdaki bölümde görülen) noktaya göre simetrik nokta formülünü kullanırız. Sonuç, aradığımız simetrik noktadır.

Bir doğruya göre simetri noktasının hesaplanması örneği

Başka bir noktanın bir doğruya göre simetri noktasını nasıl hesaplayacağımızı öğrendikten sonra örnek olarak çözülmüş bir alıştırma göreceğiz:

A noktasının r doğrusuna göre simetrik noktasını bulun. Nokta ve çizgi söyleniyor:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

Öncelikle A noktasından geçen r doğrusuna dik olan düzlemi hesaplamamız gerekiyor. Bu düzleme normal olan vektör, bileşenleri parametrenin önündeki terimler olan doğrunun yön vektörü olacaktır.

$t$

çünkü parametrik denklemler şeklinde ifade edilir:

$\vv{n}=(1,4,-3)$

Ve bir düzlemin denkleminin A, B ve C katsayıları normal vektörünün koordinatlarıyla çakışır, dolayısıyla:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

A noktası bu düzlemde yer almalıdır, dolayısıyla D katsayısını bulmak için artık A noktasını düzlem denkleminde yerine koyabiliriz:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

Böylece A noktasından geçen ry doğrusuna dik olan düzlemin denklemi şöyle olur:

$\pi : \ x+4y-3z-7=0$

Düzlemin denklemini öğrendikten sonra düzlem ile doğrunun kesişme noktasını hesaplamamız gerekir. Bunu yapmak için doğrunun koordinatlarını düzlem denkleminde yerine koyarız ve ortaya çıkan denklemi çözeriz:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

Şimdi değerini değiştiriyoruz

$t$

çizginin denkleminde elde edilir:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

Dolayısıyla r doğrusu ile ona dik olan düzlem arasındaki kesişme noktası şöyledir:

$M(0,1,-1)$

Son olarak A noktasının M noktasına göre simetrik noktasını bulmak yeterlidir; Bunun için bu sayfanın başında görülen formülü kullanabiliriz:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

bir düzleme simetrik nokta

Başka bir noktanın bir düzleme göre simetri noktasını belirleme yöntemini görmeden önce tanımının ne olduğuna bakalım:

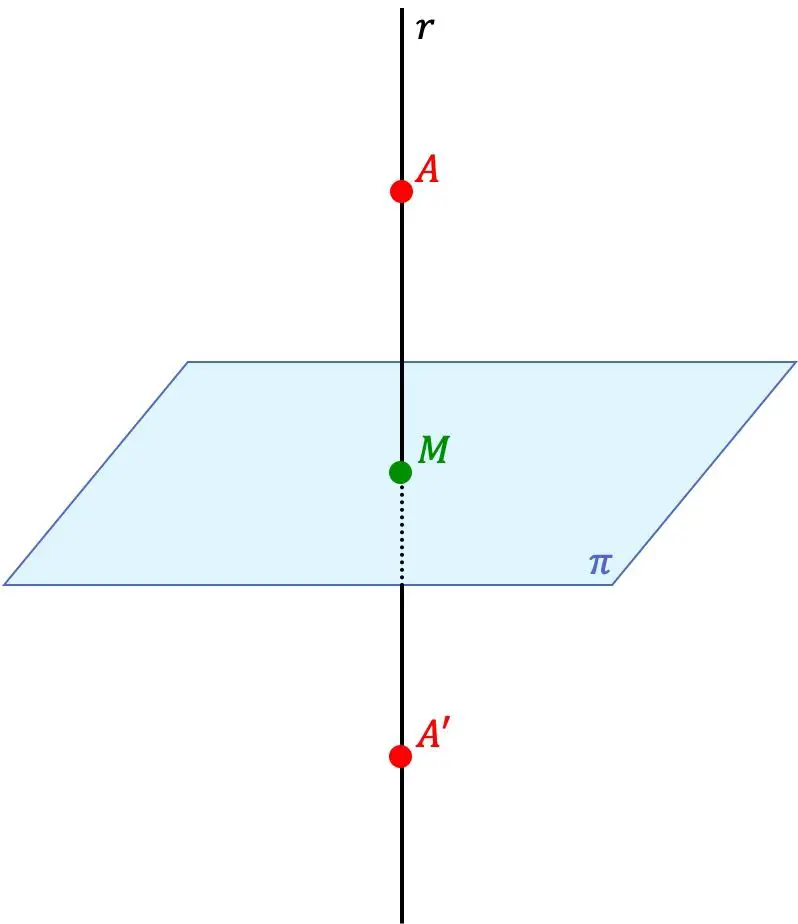
A’ noktası, iki A’ ve A noktası düzleme dik olarak aynı çizgi üzerinde yer alıyorsa ve ayrıca A’ noktası ile düzlem arasındaki mesafe mesafeye eşitse, A noktasının bir düzleme göre simetrik noktasıdır. A noktası ile düzlem arasındadır.

bir düzleme göre başka bir noktaya simetrik nokta

$d(A,\pi)= d(A',\pi)$

Yani düzlem aynı zamanda iki nokta arasındaki simetri düzlemidir.

Bu nedenle, A noktasının simetrik noktasının π düzlemine göre Kartezyen koordinatlarını bilmek için aşağıdaki adımları izlemelisiniz:

A noktasından geçen düzleme dik doğrunun denklemini buluyoruz. Bunun için doğrunun yön vektörü olarak düzleme dik vektörü kullanacağız.
Düzlem ile bulunan çizgi arasındaki kesişme noktasını hesaplıyoruz (önceki görüntünün M noktası).
A noktasının M noktasına göre simetrik noktasını bulmak için (başlangıçta görülen) noktaya göre simetrik nokta formülünü kullanırız. Sonuç, aradığımız simetrik noktadır.

Bir düzleme göre simetri noktasını belirleme örneği

Aşağıda başka bir noktanın düzleme göre simetri noktasıyla ilgili çözülmüş bir problem görebilirsiniz:

A’nın π düzlemine göre simetri noktasını belirleyin. Nokta ve planı söyledikten sonra:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

Yapmamız gereken ilk şey, düzleme dik olan ve A noktasından geçen doğrunun denklemini bulmaktır. Bunun için bileşenleri X olan doğrunun yön vektörü olarak düzleme dik vektörü kullanabiliriz, Y, Z, düzlem denkleminin sırasıyla A, B ve C terimlerinin katsayılarıdır:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$