Düzlemin örtülü, genel veya Kartezyen denklemi

Genel veya Kartezyen denklem olarak da bilinen örtülü düzlem denkleminin (formül) nasıl hesaplandığına ilişkin açıklama. Ayrıca düzlemin denklemini normal vektörden nasıl bulacağınızı da öğreneceksiniz. Dahası, adım adım çözülen örnekleri ve alıştırmaları görebileceksiniz.

Planın örtülü veya genel denklemi nedir?

Analitik geometride, düzlemin genel veya Kartezyen denklemi olarak da adlandırılan bir düzlemin örtülü denklemi , herhangi bir düzlemin matematiksel olarak ifade edilmesini sağlayan bir denklemdir. Bir düzlemin örtülü veya genel denklemini bulmak için bir noktaya ve o düzleme ait iki doğrusal bağımsız vektöre ihtiyacımız var.

Planın örtülü veya genel denkleminin formülü

Bir düzlemin bir nokta ve iki yön vektörünü düşünün:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Bir düzlemin örtülü, genel veya Kartezyen denklemi, aşağıdaki determinantın çözülmesi ve sonucun 0’a eşitlenmesiyle elde edilir:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Böylece ortaya çıkan planın örtülü veya genel denklemi aşağıdaki gibi olacaktır:

$Ax+By+Cz+D=0$

Formüldeki iki vektörün birbirinden doğrusal olarak bağımsız olması yani farklı yönlere sahip olması önemlidir. Ve bu koşulun karşılanması için iki vektörün paralel olmaması yeterlidir.

r3'teki pan xy'nin örtülü veya genel veya Kartezyen denklemi

Bu formülün nedenini bilmek gerekli olmasa da aşağıda gösterimini görebilirsiniz.

Bir planın parametrik denklemlerinden başlayarak planın örtülü (veya genel) denklemine geçeceğiz:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

İlk olarak, her bir parametrik denklemin bağımsız terimini denklemin diğer tarafına aktarıyoruz:

$\displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Veya eşdeğer:

$\displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}$

Yukarıdaki denklem sisteminin uygun bir çözüme sahip olması için aşağıdaki matrisin sıralamasının 2’ye eşit olması gerekir (Rouche-Frobenius teoremi):

$\displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}$

Yani önceki matrisin aralığının iki olması gerekiyorsa, 3×3 determinantının da mutlaka sıfıra eşit olması gerekir:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Ve bu determinantı çözerek bir düzlemin genel, örtülü veya Kartezyen denklemini elde ederiz:

$Ax+By+Cz+D=0$

Yani, düzlemin örtülü (veya genel) denklemini ve parametrik denklemlerini az önce gördük, ancak bir düzlemi analitik olarak ifade etmenin vektör denklemi ve kanonik denklem gibi daha birçok yolu vardır. Plandaki tüm denklemlerin formülünü ve açıklamasını bu linkte görebilirsiniz.

Düzlemin örtülü veya genel denkleminin nasıl bulunacağına ilişkin örnek

Bir düzlemin örtülü (veya genel veya Kartezyen) denkleminin nasıl belirleneceğini bir örnek üzerinden görelim:

Noktadan geçen düzlemin örtülü veya genel denklemini bulun
$P(3,1,-1)$

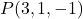
ve vektörleri içerir

$\vv{\text{u}}=(2,0,3)$

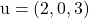
Ve

$\vv{\text{v}}=(4,-1,2).$

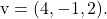
Düzlemin genel veya örtülü denklemini hesaplamak için, noktanın iki vektörü, değişkenleri ve koordinatlarından oluşan aşağıdaki determinantın çözülmesi gerekir:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Böylece vektörleri ve noktayı formülde yerine koyarız:

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0$

$\displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0$

Ve şimdi 3. derecenin determinantını örneğin Sarrus kuralıyla veya eşçarpanlar (veya yardımcılar) aracılığıyla çözüyoruz:

$-2(z+1)+12(y-1)+3(x-3)-4(y-1) = 0$

Şimdi terimleri işletiyor ve gruplandırıyoruz:

$3(x-3)+8(y-1) -2(z+1) = 0$

$3x-9+8y-8 -2z-2 = 0$

$3x+8y-2z-19 = 0$

Bu nedenle planın örtülü veya genel denklemi şöyledir:

$\bm{3x+8y-2z-19 = 0}$

Bir düzlemin örtülü veya genel denklemini normal vektöründen hesaplayın

Düzlem denklemlerindeki çok tipik bir problem, verilen bir nokta ve onun normal (veya dik) vektörü verilen bir düzlemin denkleminin neye benzediğini bulmaktır. Peki nasıl çalıştığını görelim.

Ancak öncelikle bir düzleme dik vektörün X, Y, Z bileşenlerinin , söz konusu düzlemin örtülü (veya genel) denkleminin sırasıyla A, B, C katsayılarıyla çakıştığını bilmelisiniz.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Altın

$\vv{n}$

vektör düzleme dik mi

$\pi.$

Önceki ilişkiyi öğrendikten sonra, bu tür düzlem denklem problemlerini çözmenin bir örneğini görelim:

Noktadan geçen düzlemin örtülü veya genel denklemini belirleyin
$P(1,0,-2)$

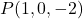
ve normal vektörlerinden biri

$\vv{n}=(3,-1,2) .$

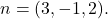
Bir düzlemin örtülü, genel veya Kartezyen denkleminin formülü şöyledir:

$Ax+By+Cz+D=0$

Böylece normal vektörden A, B ve C katsayılarını bulabiliriz çünkü bunlar normal vektörünün bileşenlerine eşdeğerdir:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

Ancak sadece D parametresini bulmamız gerekiyor. Bunun için düzleme ait noktanın koordinatlarını denklemde yerine koyuyoruz:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

Yani planın örtülü veya genel denklemi şöyledir:

$\bm{3x-y+2z+1 = 0}$

Düzlemin örtülü veya genel denklemiyle ilgili çözülmüş problemler

1. Egzersiz

Noktadan geçen düzlemin örtülü veya genel denklemini bulun

$P(-2,1,3)$

ve vektörleri içerir

$\vv{\text{u}}=(4,1,3)$

$\vv{\text{v}}=(5,3,-1).$

Çözüme bakın

Düzlemin genel veya örtülü denklemini hesaplamak için iki vektör, üç değişken ve noktanın koordinatlarından oluşan aşağıdaki determinantı çözmek gerekir:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Böylece vektörleri ve noktayı formülde yerine koyarız:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

Şimdi 3×3 matrisin determinantını seçtiğiniz yöntemle çözüyoruz:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Son olarak işlemleri gerçekleştirip benzer terimleri gruplandırıyoruz:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Yani planın örtülü veya genel denklemi şöyledir:

$\bm{-8x+11y+7z-20 = 0}$

Alıştırma 2

Noktanın olup olmadığını belirleyin

$P(-1,5,-3)$

aşağıdaki plana aittir:

$\pi : \ 2x+y+6z-5=0$

Çözüme bakın

Noktanın düzlemde olabilmesi için denkleminin doğrulanması gerekir. Bu nedenle, noktanın Kartezyen koordinatlarını düzlem denkleminde yerine koymamız ve denklemin yerine getirilip getirilmediğini kontrol etmemiz gerekir:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

Nokta düzlemin denklemine uymadığından bu düzlemin parçası değildir.

Alıştırma 3

Aşağıdaki üç noktayı içeren planın örtülü (veya genel) denklemini bulun:

$A(5,-1,-2) \qquad B(2,1,3) \qquad C(4,1,-2)$

Çözüme bakın

Düzlemin örtülü denklemini bulmak için düzleme bağlanan iki doğrusal bağımsız vektör bulmamız gerekir. Bunun için de 3 noktayla tanımlanan iki vektörü hesaplayabiliriz:

$\vv{AB} = B - A = (2,1,3) - (5,-1,-2) = (-3,2,5)$

$\vv{AC} = C - A = (4,1,-2) - (5,-1,-2) = (-1,2,0)$

Bulunan iki vektörün koordinatları orantılı değildir, dolayısıyla birbirlerinden etkili bir şekilde doğrusal olarak bağımsızdırlar.

Artık düzlemin iki yön vektörünü ve bir noktasını zaten biliyoruz, dolayısıyla düzlemin genel denklemi için formülü zaten uygulayabiliriz:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Vektörleri ve üç noktadan birini formülde yerine koyarız:

$\displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0$