▷ Sonsuzdaki limitler nasıl çözülür (+25 alıştırma çözüldü)

Burada sonsuzda her türlü limitin nasıl çözüleceğini bulacaksınız: polinom, rasyonel, üstel fonksiyonlar, köklü fonksiyonlar, sonsuzda belirsizlikler… Ayrıca, x olduğunda limitlerle ilgili adım adım çözülen 25 alıştırma ile antrenman yapabileceksiniz. sonsuzluğa yönelmek. .

X sonsuza doğru gittiğinde bir fonksiyonun limiti

Bir fonksiyonun x sonsuza yaklaşırken limiti , ister pozitif ister negatif olsun, gerçek bir değer olabilir, artı sonsuz, eksi sonsuz olabilir veya hiç olmayabilir. Sonsuzdaki limitleri çözmek için x’i sonsuzla değiştirmeniz gerekir.

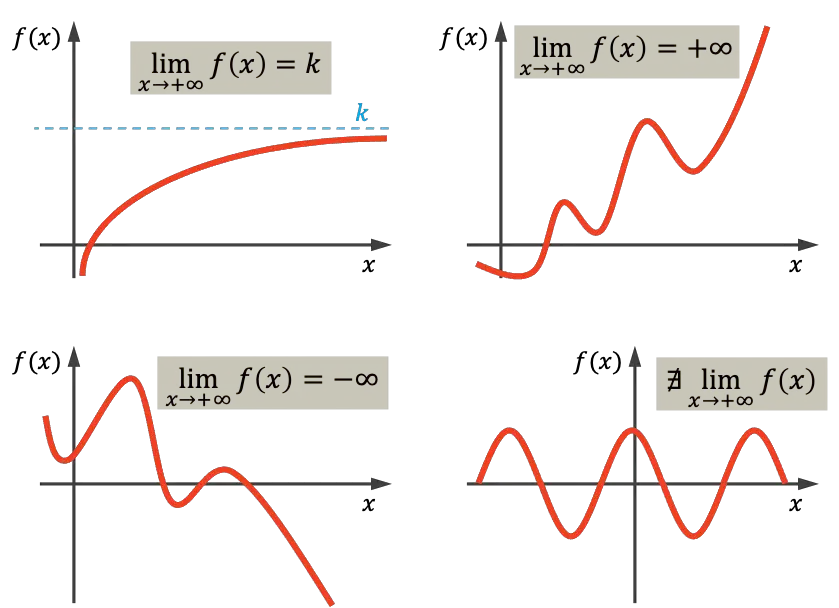
İlk grafikten de görebileceğiniz gibi, gösterilen fonksiyon, x büyüdükçe k’ye yaklaştığından, k gerçek değerine doğru sonsuza doğru yönelir. Sağ üstteki fonksiyon, x sonsuza yaklaştıkça sonsuza doğru yönelir, çünkü x’in değeri arttıkça sonsuza kadar büyür. Öte yandan sol alttaki grafik durmadan azalıyor ve dolayısıyla eksi sonsuza doğru yöneliyor. Son olarak son fonksiyon periyodiktir ve herhangi bir değere yönelmediğinden bu durumda sonsuzluğun sınırı yoktur.

Sonsuzdaki limitler nasıl çözülür?

Polinom fonksiyonlarda sonsuzluğa giden bir limiti çözmek için, x’i yalnızca fonksiyonun en yüksek dereceli teriminde sonsuzla değiştirmeliyiz.

Örneğin, en yüksek dereceden tek terimli sayının yerine yalnızca sonsuzluğu koyduğumuz aşağıdaki sonsuzluğa limit hesaplamasına bakın:

$\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}$

Örnekte görebileceğiniz gibi +∞ karesi +∞ verir, çünkü çok büyük bir sayının (+∞) 2’nin üssü her zaman çok büyük bir sayı (+∞) verir.

Aynı şey çarpma işleminde de olur: Eğer çok büyük bir sayıyı (+∞) çarparsanız, her zaman çok büyük bir sayı (+∞) elde edersiniz. Örneğin:

$3\cdot (+\infty)= +\infty.$

Uyarı: Sonsuza kadar olan limitleri hesaplamak için aşağıdaki unsurları dikkate almak önemlidir:

→ Çift üslü olan negatif bir sayı pozitiftir. Bu nedenle, eksi sonsuzun çift üs değerine yükseltilmesi artı sonsuzluğu verir:

$(-\infty)^2 = +\infty$

→ Tek üslü olan negatif bir sayı negatiftir. Bu nedenle, tek bir üsse yükseltilen eksi sonsuz eksi sonsuzdur:

$(-\infty)^3 = -\infty$

→ Negatif bir sayının çarpılması sonsuzluğun işaretini değiştirir:

$-2(+\infty) = - \infty$

→ Herhangi bir sayının bölümü

$\pm \infty$

0 verir:

$\cfrac{5}{\infty} = 0$

Sonsuzluğa sınır örnekleri

Böylece polinomlarda sonsuzluğun sınırlarının nasıl çözüldüğünü görebilirsiniz; aşağıda bu türden birkaç çözümün çözümü verilmiştir:

$\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}$

Sonsuzluğun belirsiz sınırları

Sonsuzluğun sınırlarını hesaplamak her zaman o kadar kolay olmayacaktır, çünkü bazen sonsuzluk arasındaki sonsuzluğun belirsizliğini veya sonsuz eksi sonsuzun belirsizliğini elde edeceğiz.

$\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty$

Bu tür belirsizlikler (veya belirsiz formlar) elde ettiğimizde sonucu doğrudan bilemeyiz, bunun yerine sınır değerini bulmak için bir ön işlem yapmamız gerekir. Daha sonra sonsuzdaki belirsiz limitlerin nasıl çözümlendiğini göreceğiz.

Sonsuz arasında sonsuz belirsizlik

Belirsizlik sonsuzluğunun sonsuza bölünmesinin sonucunu bulmak için kesrin payının derecesi ile paydasının derecesini karşılaştırmamız gerekir:

Pay polinomunun derecesi payda polinomunun derecesinden küçükse, sonsuz üzerindeki sonsuz belirsizlik sıfıra eşittir.
Pay polinomunun derecesi payda polinomunun derecesine eşdeğerse, sonsuzluğa karşı sonsuz belirsizlik , iki polinomun temel katsayılarının bölümüdür.
Pay polinomunun derecesi payda polinomunun derecesinden büyükse, sonsuzluk arasındaki sonsuz belirsizlik az ya da çok sonsuzluk verir (işaret, iki polinomun ana terimlerine bağlıdır).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> Örneğin aşağıdaki limitte pay polinomu ikinci dereceden, payda polinomu ise üçüncü dereceden olduğundan limitin çözümü 0’dır. <p class=$ $\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Rasyonel fonksiyonun iki polinomunun ikinci dereceden olduğu diğer örneğe bakın, dolayısıyla sonsuzdaki limiti hesaplamak için yüksek dereceli terimlerin katsayılarını bölmemiz gerekir.

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Son olarak, bir sonraki limitte payın fonksiyonu paydanınkinden daha büyük bir dereceye sahiptir, dolayısıyla sonsuzun sonsuz üzerindeki belirsizliği sonsuzluğu verir. Ayrıca paydan pozitif bir sonsuzluk, paydadan ise negatif bir sonsuzluk elde edilir, dolayısıyla limitin sonucu negatiftir (negatifin arasındaki pozitif negatiftir).

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Köklü sonsuzluk arasında sonsuz belirsizlik

Öte yandan, irrasyonel bir fonksiyonun derecesi (köklü fonksiyon), ana terimin derecesi ile radikalin indeksi arasındaki bölümdür.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Dolayısıyla köklü bir fonksiyonun limiti sonsuzluk arasında sonsuz belirsizlik veriyorsa , yukarıda pay ve paydanın derecelerine ilişkin açıklanan kuralların aynısını, kökleri olan bir polinomun derecesinin farklı hesaplandığını dikkate alarak uygulamalıyız.

Köklü bir fonksiyonun sonsuz limitine ilişkin aşağıdaki örneğe bakın:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Payın derecesi 2, paydanın derecesi 4 (8/2=4) olduğundan payın derecesi paydanın derecesinden küçük olduğundan limit 0’dır.

Üstel fonksiyonlarla sonsuz arasında sonsuz belirsizlik

Üstel bir fonksiyonun büyümesi, bir polinom fonksiyonunun büyümesinden çok daha büyüktür, bu nedenle üstel bir fonksiyonun derecesinin, bir polinom fonksiyonunun derecesinden daha büyük olduğunu dikkate almalıyız.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Dolayısıyla, eğer belirsizlik sonsuzunun sonsuza bölümü üstel fonksiyonlara sahip bir limitten kaynaklanıyorsa, pay ve paydanın derecelerini açıklayan aynı kuralları uygulamalıyız, ancak üstel bir fonksiyonun bir polinomdan daha yüksek mertebede olduğunu hesaba katmalıyız. Ayrıca bölümün pay ve paydasında üstel fonksiyonlarımız varsa, tabanı en büyük olan üstel fonksiyon en yüksek mertebeden olan fonksiyon olacaktır. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

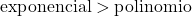
Bu örnekte payda üstel bir fonksiyondan oluşturulduğundan paydan daha yüksek mertebededir. Dolayısıyla sonsuzlar arasındaki belirsiz form sonsuz 0 verir.

Sonsuz eksi sonsuz belirsizlik

Sonsuz eksi sonsuz belirsizliğin çözümü, fonksiyonun kesirli veya köklü olmasına bağlıdır. Şimdi bu iki farklı durum için bu tür belirsizliği nasıl çözebileceğimizi görelim.

Kesirlerde belirsizlik sonsuz eksi sonsuz

Cebirsel kesirlerin toplanmasında veya çıkarılmasında sonsuz eksi sonsuz belirsizlik oluştuğunda , önce kesirlerde toplama veya çıkarma işlemi yapmamız, sonra limiti hesaplamamız gerekir.

Bir örneği adım adım çözerek kesirli bir fonksiyonda belirsizlik sonsuz eksi sonsuzun nasıl hesaplanacağını görelim:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

İlk önce limiti hesaplamaya çalışıyoruz:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Ancak ∞-∞ belirsizliğini elde ederiz.

Önce kesirleri çıkarmamız gerekiyor. Bunu yapmak için kesirleri ortak bir paydaya indiririz, yani bir kesirin payını ve paydasını diğerinin paydasıyla çarparız:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

Artık iki kesirin paydası aynı olduğuna göre bunları tek bir kesirde birleştirebiliriz:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

Pay ve payda üzerinde işlem yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

Ve son olarak limiti tekrar hesaplıyoruz:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Bu durumda sonsuzluk arasındaki sonsuz belirsizlik +∞ verir çünkü payın derecesi paydanın derecesinden büyüktür.

Belirsizlik sonsuz eksi köklerle sonsuz

Radikal toplama veya çıkarma işleminde sonsuz eksi sonsuz belirsizlik oluştuğunda , önce fonksiyonu eşlenik radikal ifadeyle çarpmalı ve bölmeli, sonra limiti çözmeliyiz.

İrrasyonel bir fonksiyonda sonsuz eksi sonsuzun belirsizliğini adım adım bir örnekle nasıl çözeceğimizi görelim:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

İlk önce fonksiyonun limitini radikallerle çözmeye çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

Ancak ∞-∞ belirsiz formunu elde ederiz. Yani sonsuz eksi sonsuzun ne kadar belirsizlik olduğunu bilmek için açıklanan prosedürü uygulamanız gerekir.

Fonksiyonun kökleri olduğundan, fonksiyonun tamamını birleşik irrasyonel ifadeyle çarpar ve böleriz:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

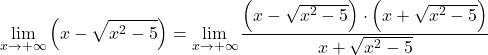
Payın cebirsel ifadesi, bir toplamın ve bir farkın çarpımının dikkate değer özdeşliğine karşılık gelir; bu nedenle ifadeyi basitleştirebiliriz:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

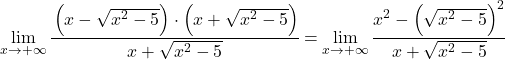
Şimdi karesi alındığı için limitin kökünü basitleştiriyoruz:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

Kesirin payı üzerinde işlem yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

Ve son olarak limit hesaplamasını yeniden yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

Dolayısıyla limitin sonucu 0’dır çünkü her sayının sonsuza bölümü sıfıra eşittir.

Sonsuzda limitlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Grafik fonksiyonunun aşağıdaki limitlerini bulun:

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

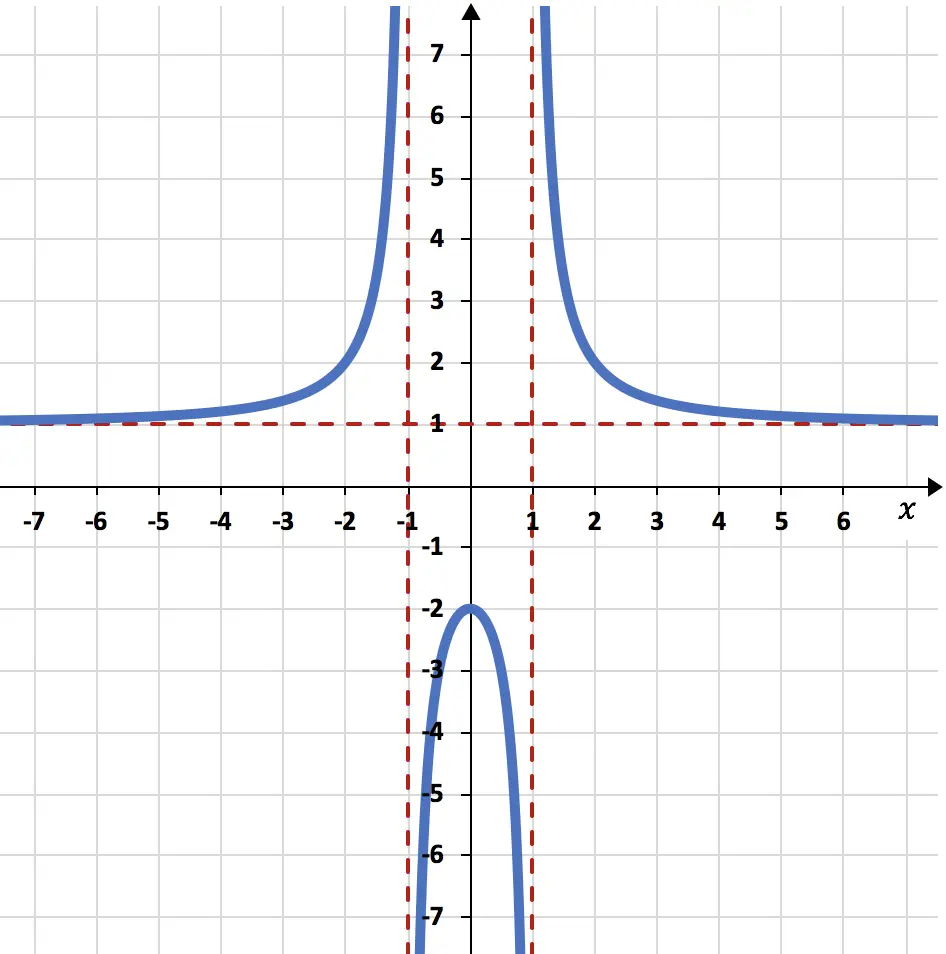
Bir fonksiyonun temsilinden sonsuza kadar sınırlar

Çözümü görün

X eksi sonsuza ve artı sonsuza doğru yöneldiğinde fonksiyonun limiti 1 verir:

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

Fonksiyonun x=-1 noktasında sol ve sağdaki yanal limitleri sırasıyla artı sonsuz ve eksi sonsuzdur:

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

Son olarak, x 1’e doğru gittiğinde fonksiyonun yanal limitleri eksi sonsuz ve artı sonsuz değerindedir:

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

Alıştırma 2

Aşağıdaki fonksiyonun x artı sonsuzuna yaklaşırken limitini çözün:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

Çözümü görün

Sonsuzdaki limiti bulmak için polinomun en yüksek dereceli terimindeki x’i sonsuzla değiştirmemiz gerekir:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

Alıştırma 3

Aşağıdaki polinom fonksiyonunun sonsuzluğa olan sınırını hesaplayın:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

Çözümü görün

Sonsuzdaki limiti bulmak için polinomun en yüksek dereceli terimindeki x’i sonsuzla değiştiririz ve hesaplamaları yaparız:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

Alıştırma 4

Aşağıdaki polinom fonksiyonunun en az sonsuz limitini çözün:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

Çözümü görün

Sonsuzdaki limiti hesaplamak için polinomun en yüksek dereceli terimindeki x’i eksi sonsuzlukla değiştiririz ve fonksiyonu değerlendiririz:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

Eksi sonsuzun karesi olduğundan sonsuzluğun işareti pozitif olur.

Alıştırma 5

Aşağıdaki rasyonel fonksiyonun sonsuzdaki limitini bulun:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

Çözümü görün

Sonsuzluğun sınırını belirlemek için, kesrin pay ve paydasının en yüksek derecesinin teriminde x’i artı sonsuzlukla değiştiririz:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

Artı veya eksi sonsuza bölünen herhangi bir sayının 0’a eşit olduğunu unutmayın.

Alıştırma 6

Aşağıdaki limiti sonsuzda çözün:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

Çözümü görün

X, bir fonksiyonun ±∞ yönünde eğilim gösterdiğinde limiti hesaplamak için, fonksiyonun en yüksek derecesinin tek terimlisine bakmanız yeterlidir:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

Egzersiz 7

x negatif sonsuza yaklaşırken aşağıdaki fonksiyonun limitini hesaplayın:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

Çözümü görün

Bu durumda ikinci dereceden terimin yerine sonsuzluğu koymak yeterlidir:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

Egzersiz 8

x sonsuza yaklaşırken aşağıdaki üstel fonksiyonun limitini bulun:

$\displaystyle \lim_{x \to +\infty} 2^x$

Çözümü görün

Üstel bir fonksiyon olmasına rağmen limiti çözme süreci aynıdır: x’in yerine sonsuzu yazın.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

Egzersiz 9

Aşağıdaki üstel fonksiyonun sonsuz limitini çözün:

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

Çözümü görün

Bu sınırı çözmek için kesirlerin özelliklerini kullanmanız gerekir:

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

Egzersiz 10

Aşağıdaki limiti sonsuzda çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Çözümü görün

Limit, artı sonsuz arasındaki belirsizliği eksi sonsuzluğu verir. Payın derecesi paydanın derecesinden büyüktür, dolayısıyla belirsiz limit artı sonsuza eşittir. Ancak negatif sonsuzun pozitif sonsuza bölünmesi nedeniyle sonuç negatif sonsuzdur.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Egzersiz 11

Aşağıdaki belirsiz sınırı düzeltin:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Çözümü görün

Bu problemde, sonsuz/sonsuz belirsiz formu, aynı dereceden iki polinomun bölümünden elde edilir, dolayısıyla belirsiz limitin sonucu, bunların ana katsayılarının bölümüdür:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Egzersiz 12

Aşağıdaki limiti en az sonsuza kadar hesaplayın:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Çözümü görün

Payın cebirsel ifade derecesi paydanın ifade derecesinden küçüktür, dolayısıyla +∞/+∞ belirsizliği 0 verir:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Egzersiz 13

Kökleri olan bir fonksiyonun aşağıdaki belirsiz limitini çözün:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Çözümü görün

Payın ifadesi radikalin altındadır, dolayısıyla derecesi 7/3’tür. Öte yandan, payda polinomu ikinci derecedendir. Ve 7/3>2 olduğundan limit daha fazla sonsuzluk verir:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Egzersiz 14

Aşağıdaki fonksiyonun kesirli sonsuz limitini belirleyin:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Çözümü görün

Bu alıştırmada payın derecesi paydanın derecesinden büyük olacak şekilde belirsizlik eksi sonsuz bölü eksi sonsuz elde edeceğiz, dolayısıyla:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Egzersiz 15

Aşağıdaki fonksiyonun en az sonsuz limitini bulun:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Çözümü görün

Payda polinomu ikinci dereceden, pay polinomu ise doğrusaldır. Bu nedenle sonsuz belirsizliğin sonsuza bölümü 0 verir.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Egzersiz 16

Aşağıdaki fonksiyonun en az sonsuz limitini çözün:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Çözümü görün

Pay, paydadan bir derece büyüktür, dolayısıyla belirsiz ∞/∞ formunun sonucu sonsuz olacaktır. Ek olarak, sonsuzluk işareti negatif olacaktır çünkü negatif arasındaki pozitif, negatife dönüşür:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Egzersiz 17

Aşağıdaki limiti sonsuzda çözün:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Çözümü görün

Üstel fonksiyon polinom fonksiyonundan daha yüksek mertebede olduğundan limit sonsuzluğu verecektir. Ancak pozitifi negatife böldüğümüzde sonsuzluk işareti negatif olacaktır:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Egzersiz 18

Aşağıdaki fonksiyonun sonsuz limitini karekökle hesaplayın:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

Çözümü görün

Pay karekökten oluştuğu için derecesi 2/2=1 olur. O halde payın derecesi paydanın derecesine eşit olduğundan sonsuzluk arasındaki sonsuz belirsizlik şu şekilde çözülür:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

Egzersiz 19

Aşağıdaki fonksiyonun sonsuz limitini iki radikalle çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Çözümü görün

Payın derecesi 7/3=2,33, paydanın derecesi 5/2=2,5’tir. Dolayısıyla payın derecesi paydanın derecesinden küçük olduğundan sonsuz arasındaki belirsiz sonsuz sınır 0’dır:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Egzersiz 20

Aşağıdaki limiti hesaplayın:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Çözümü görün

Payın derecesi ne olursa olsun, paydada üstel bir fonksiyona sahip olduğumuz için, sonsuz bölü sonsuzun belirsiz formunun sonucu 0’dır:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Egzersiz 21

Aşağıdaki rasyonel fonksiyonun sonsuz limitini belirleyin:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Çözümü görün

Öncelikle fonksiyona sonsuzluğu koyarak limiti hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Fakat ∞ – ∞ belirsizliğini buluyoruz. Bu nedenle kesirleri ortak bir paydaya indiriyoruz:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

Artık iki kesir aynı paydaya sahip olduğundan, bunları tek bir kesirde birleştirebiliriz:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

Payın parantezlerini yapıyoruz:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

Ve son olarak limiti belirliyoruz:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

Bu durumda ∞/∞ belirsizliği +∞ verir çünkü payın derecesi paydanın derecesinden büyüktür.

Egzersiz 22

Aşağıdaki kesirli fonksiyonun limitini x 0’a yaklaşırken çözün:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Çözümü görün

Öncelikle limiti her zamanki gibi hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Ancak ∞-∞ belirsiz formunu elde ederiz. Bu nedenle fonksiyonun kesirlerini ortak bir paydaya indirmeliyiz.

Bu durumda, x ⁴ , x ^2’nin bir katıdır, dolayısıyla ikinci kesirin pay ve paydasını x ² ile çarparak her iki kesrin de aynı paydaya sahip olmasını sağlayacağız:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Artık iki kesri çıkarabiliriz:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Limiti tekrar çözmeye çalışıyoruz:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Ancak sıfırdan başlayan bir sabitin belirsizliğiyle sonuçlanırız. Bu nedenle fonksiyonun yanal sınırlarını hesaplamak gerekir.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

Sonuç olarak, fonksiyonun x=0 noktasındaki iki yanal limiti -∞ verdiğinden limitin çözümü -∞ olur:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Egzersiz 23

Aşağıdaki fonksiyonun sonsuz limitini köklerle çözün:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Çözümü görün

Limiti çözmeye çalışırken, belirsizlik sonsuz eksi sonsuzluğu elde ederiz:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Bu nedenle, fonksiyonda radikaller bulunduğundan, eşlenik radikal ifadeyle çarpılıp bölünmelidir:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

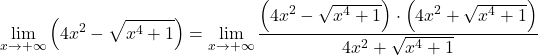
Payda, kareler farkına eşit olan bir toplam ve farkın dikkate değer çarpımına sahibiz. Henüz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

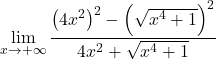
Radikalleri kareye sadeleştiriyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

Pay üzerinde çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

Ve sonunda sınırı buluyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

Bu durumda, payın derecesi paydanın derecesinden daha büyük olduğundan belirsizlik sonsuzunun sonsuza bölümü daha sonsuzdur (karekökün dereceyi iki oranında azalttığını hatırlayın:

$\sqrt{x^4} = x^{4/2} = x^2$

Egzersiz 24

Aşağıdaki irrasyonel fonksiyonun x sonsuza yaklaşırken limitini çözün:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Çözümü görün

Öncelikle limiti her zamanki gibi hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Ancak bu, sonsuzlukların farkının belirsizliğiyle sonuçlanır. Bu nedenle, fonksiyonun kökleri olduğundan, ifadeyi eşlenik radikalle çarpmalı ve bölmeliyiz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

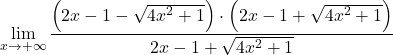
Kesir payının dikkate değer eşitliğini gruplandırıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

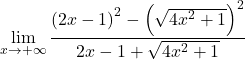
Karekökü çözüyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Bir farkın karesinin dikkate değer kimliğini çözüyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Pay üzerinde çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

Ve son olarak sonsuzdaki limitin değerini hesaplıyoruz:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Paydada x kare olsa da bir kökün içinde olduğu için derecesi aslında 1’dir:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Dolayısıyla -∞/+∞ belirsizliğinin sonucu, payın derecesi paydanın derecesi ile aynı olduğundan, en yüksek derecedeki x’in katsayılarının bölümüdür.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Paydada birinci dereceden iki terim olduğundan

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

-∞/+∞ belirsizliğini çözmek için birinci dereceden terimlerin tüm katsayılarını almak gerekir, yani

$2$

ile ilgili

$2x$

$\sqrt{4}$

ile ilgili

$\sqrt{4x^2}.$

Egzersiz 25

Aşağıdaki kesirli fonksiyonun x’i 1’e yaklaşırken limitini hesaplayın:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

Çözümü görün

Limiti yapmaya çalışarak sonsuzluğun belirsiz limiti eksi sonsuzu elde ederiz:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Bu nedenle kesirleri ortak bir paydaya indirmeliyiz, yani bir kesrin payını ve paydasını diğerinin paydasıyla çarpmamız gerekir:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

Artık iki kesirin paydası aynı olduğundan, onları bir araya getirebiliriz:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Biz şunları işletiyoruz:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

Ve yine limiti çözmeye çalışıyoruz:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Ama belirsizlik sıfırını sıfıra bölerek buluyoruz. Bu nedenle pay ve paydanın polinomlarını çarpanlarına ayırmamız gerekir:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Şimdi pay ve paydada tekrarlanan faktörü çıkararak kesri basitleştiriyoruz:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

Ve son olarak limiti çözüyoruz:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Sonsuzluğa kadar sınırlar

X sonsuza doğru gittiğinde bir fonksiyonun limiti

Sonsuzdaki limitler nasıl çözülür?

Sonsuzluğa sınır örnekleri

Sonsuzluğun belirsiz sınırları

Sonsuz arasında sonsuz belirsizlik

Köklü sonsuzluk arasında sonsuz belirsizlik

Üstel fonksiyonlarla sonsuz arasında sonsuz belirsizlik

Sonsuz eksi sonsuz belirsizlik

Kesirlerde belirsizlik sonsuz eksi sonsuz

Belirsizlik sonsuz eksi köklerle sonsuz

Sonsuzda limitlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Egzersiz 7

Egzersiz 8

Egzersiz 9

Egzersiz 10

Egzersiz 11

Egzersiz 12

Egzersiz 13

Egzersiz 14

Egzersiz 15

Egzersiz 16

Egzersiz 17

Egzersiz 18

Egzersiz 19

Egzersiz 20

Egzersiz 21

Egzersiz 22

Egzersiz 23

Egzersiz 24

Egzersiz 25

Yorum bırakın Yanıtı iptal et