Bu sayfada çevre denklemi hakkında her şeyi bulacaksınız: adi denklem, genel denklem, diğer çevre denklemi türleri, çevre denklemi doğru olduğunda… Ayrıca denklemin nasıl bulunacağına dair örnekler göreceksiniz. bir çevre ve çözülmüş alıştırmalarla pratik yapabilirsiniz.
Çemberin sıradan denklemi
Çevre denkleminin ne olduğunu görmeden önce çevre kavramını hatırlayalım:
Çevre, düzlem üzerinde merkez adı verilen sabit bir noktadan eşit uzaklıktaki noktaların geometrik yeridir.

Bu nedenle bir çember üzerindeki tüm noktalar merkeze aynı uzaklıkta bulunur.
Ayrıca daire, elips, parabol ve hiperbolle birlikte dört konik bölümden biridir. Yani bir koninin tabanına paralel bir düzlemle kesilmesiyle bir daire elde edilebilir.
Bir daireyi Kartezyen düzlemde tanımlamanın en basit yolu onun sıradan denklemidir. Yani, sıradan çevre denkleminin formülü aşağıdaki gibidir:
Çemberin sıradan denklemi :
![]()
Altın:
-

dairenin yarıçapıdır.
-

Ve

çemberin merkezinin koordinatları:
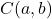
Her ne kadar biraz sıkıcı olduğu için göstermesek de bu denklem Pisagor teoreminden elde edilebilir.
Bir örnekle bir dairenin olağan denkleminin nasıl hesaplandığını görelim:
- Merkezi nokta olan 5 yarıçaplı çemberin sıradan denklemini belirleyin
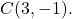
Bir dairenin sıradan denkleminin formülü:
![]()
Bu nedenle, yalnızca bilinmeyeni yerine koymamız gerekir.
![]()
yarıçapın değerine ve bilinmeyenlere göre
![]()
Ve
![]()
dairenin merkezinin sırasıyla X ve Y koordinatlarına göre:
![]()
O halde çemberin sıradan denklemi şu şekildedir:
![]()
Çemberin genel denklemi
Diğer bir çevre denklemi türü genel denklemdir, aslında en çok kullanılanıdır. Daha sonra herhangi bir çevrenin genel denkleminin sıradan denklemden nasıl elde edileceğini göreceğiz.
Bir dairenin sıradan denklemini düşünün:
![]()
Dikkate değer eşitlikler (veya dikkate değer ürünler) geliştirirsek:
![]()
![]()
Şimdi değişkenlerde 3 değişiklik yapıyoruz:
![]()
Ve son olarak çevrenin genel denklemini elde ederiz:
![]()
Dolayısıyla çevrenin genel denkleminin formülü şu şekildedir:
![]()
çemberin merkezinin olduğu yer:
![]()
Ve dairenin yarıçapı:
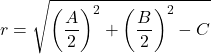
Yani bu çevre denklemi her zaman sıradan denklemle elde edilir. İşte nasıl yapıldığını görmek için bir örnek:
- Merkezi nokta olan 6 yarıçaplı çemberin genel denklemini belirleyin
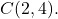
Öncelikle çemberin sıradan denklemini bulmamız gerekiyor. Bunu yapmak için formülünü kullanıyoruz:
![]()
![]()
Ve şimdi çevrenin genel denklemini bulana kadar, yani artık basitleştirme yapamayana kadar işlem yapacağız:
![]()
![]()
![]()
![]()
Buna göre çemberin genel denklemi şu şekildedir:
![]()
Problem bunu gerektirmese de artık bulduğumuz denklemin doğruluğunu kontrol etmek için merkezini ve yarıçapını hesaplayabiliriz.
Çemberin merkezini belirlemek için formülünü kullanırız:
![]()
![]()
![]()
![]()
Aslında dairenin merkezi ifadenin merkeziyle örtüşmektedir.
Ayrıca çevrenin yarıçapını formülüyle de kontrol ediyoruz:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png)
Ve yarıçap da ifadenin yarıçapına eşittir. Bu nedenle hesaplanan çevre denklemi doğrudur.
Bir çevrenin varlığı
Tüm denklemler şu şekildedir:
![]()
bir daireye karşılık gelir. Dolayısıyla bu tür bir ifadenin gerçekten bir daire denklemi olabilmesi için aşağıdaki 3 koşulun karşılanması gerekir:
- katsayıları
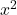
ve
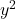
1’e eşit olmaları gerekir. Her iki değişkenin önünde birden farklı bir sayı varsa ancak her ikisi de aynı sayıya sahipse, denklemin tamamının bu sayıya bölünebileceğini ve katsayılarının 1 olacağını unutmayın.
- Denklemin bir terimi olamaz
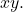
- Aşağıdaki ifade pozitif olmalıdır:
 Diğer daire denklemi türleri
Diğer daire denklemi türleri
Gördüğümüz iki daire denklemi, sıradan denklem ve genel denklem, düzlemdeki (R2’deki) bir daireyi matematiksel olarak ifade etmek için en çok kullanılanlardır. Bununla birlikte, bu geometrik nesneyi tanımlamak için çeşitli denklem türleri vardır; aşağıda her birinin açıklaması bulunmaktadır.
Çemberin kanonik denklemi
Bir dairenin kanonik denklemi veya indirgenmiş denklemi, merkezi koordinatların orijininde, yani (0,0) noktasında olan herhangi bir daireyi tanımlamak için kullanılır. Söz konusu denklem aşağıdaki gibidir:
![]()
Ek olarak yarıçap birime (1) eşit olsaydı, çevre denklemi şöyle olurdu:
![]()
Bu son denklem birim çevre veya birim çember olarak da adlandırılan gonyometrik çevreye karşılık gelir. Koordinatların orijini merkezli 1 yarıçaplı dairedir.
İki eşmerkezli dairenin denklemleri
İki eşmerkezli denklem, merkezi aynı noktada olan denklemlerdir. Ve iki eşmerkezli dairenin sahip olduğu tek farklı şey yarıçaptır.
Dolayısıyla bu koşulun karşılanması için, iki eşmerkezli dairenin denklemleri, farklı olması gereken bağımsız terimleri dışında tamamen aynıdır.
![]()
![]()
Örneğin, aşağıdaki iki daire eşmerkezlidir, çünkü bağımsız terimler dışında tüm katsayıları aynıdır:
![]()
![]()
Çemberin parametrik denklemi
Doğru gibi, bir dairenin denklemi de sinüs ve kosinüsün trigonometrik fonksiyonlarıyla parametrelendirilebilir. Böylece çemberin parametrik denklemleri şöyledir:
![Rendered by QuickLaTeX.com \diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png)
nokta nerede
![]()
çemberin merkezidir ve
![]()
Burası sizin departmanınız.
Çember denkleminin çözülmüş problemleri
1. Egzersiz
Merkezi noktadaki 5 yarıçaplı dairenin genel denklemini hesaplayın
![]()
Çemberin genel denklemini bulmak için önce onun normal denklemini bulmalıyız. Bunu yapmak için bir dairenin sıradan denkleminin formülünü kullanırız:
![]()
![]()
![]()
Adi denklemi öğrendikten sonra çemberin genel denklemini bulana kadar çalışırız:
![]()
![]()
![]()
![]()
Buna göre çemberin genel denklemi şu şekildedir:
![]()
Alıştırma 2
Aşağıdaki dairelerin her birinin merkezinin koordinatlarını ve yarıçapının uzunluğunu bulun.
![]()
![]()
![]()
çevre A)
![]()
Çevre, formülü aşağıdaki gibi olan sıradan bir denklem biçiminde ifade edilir:
![]()
Buna göre dairenin merkezinin koordinatları şöyledir:
![]()
![]()
Ve yarıçapı:
![]()
![]()
çevre B)
![]()
Bu çevre genel bir denklem biçiminde ifade edilir, dolayısıyla merkezinin koordinatlarını hesaplamak için aşağıdaki formülü kullanmanız gerekir:
![]()
![]()
![]()
![]()
Öte yandan dairenin yarıçapını bulma formülü şu şekildedir:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png)
çevre C)
![]()
Çevre, formülü aşağıdaki gibi olan sıradan bir denklem biçiminde ifade edilir:
![]()
Buna göre dairenin merkezinin koordinatları şöyledir:
![]()
Bu durumda denklemin terimi yoktur.
![]()
hiç biri
![]()
bu nedenle koordinatların kökenine odaklanmıştır:
![]()
Ve yarıçapı:
![]()
![]()
Alıştırma 3
Aşağıdaki denklemlerden hangisi çember denklemidir?
![]()
![]()
![]()
![]()
Bir ifadenin bir daire denklemi olabilmesi için aşağıdaki koşulların doğru olması gerekir:
1. Katsayılar
![]()
ve
![]()
1’e eşit olmaları gerekir.
2. Denklemin bir terimi olamaz
![]()
3.
 Bu nedenle her denklem için üç koşulun karşılandığını doğrulamamız gerekir.
Bu nedenle her denklem için üç koşulun karşılandığını doğrulamamız gerekir.
Denklem A)
![]()
katsayıları
![]()
Ve
![]()
1’dir ve denklemin terimi yoktur
![]()
Bu nedenle üçüncü koşulu kontrol etmek yeterlidir:

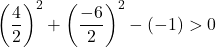
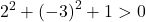
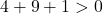
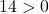 Denklem 3 koşulu da karşılıyor, dolayısıyla bir daire denklemidir.
Denklem 3 koşulu da karşılıyor, dolayısıyla bir daire denklemidir.
Denklem B)
![]()
Denklemin bir terimi var
![]()
denklemin bir daireye karşılık gelmediği.
Denklem C)
![]()
katsayıları
![]()
Ve
![]()
1 değil ama tüm terimleri bölerek denklemi dönüştürebiliriz:
![]()
Bu şekilde şimdi katsayıları
![]()
Ve
![]()
evet 1’ler ve üstelik denklemin terimi yok
![]()
Bu nedenle yalnızca üçüncü koşulu doğrulamamız gerekiyor:

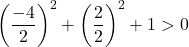
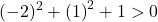
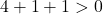
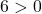 Denklem 3 koşulu da karşılıyor, dolayısıyla bir daire denklemidir.
Denklem 3 koşulu da karşılıyor, dolayısıyla bir daire denklemidir.
Denklem D)
![]()
katsayıları
![]()
Ve
![]()
1’dir ve denklemin terimi yoktur
![]()
Bu nedenle üçüncü koşulu kontrol etmek yeterlidir:

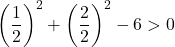
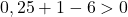
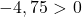 Denklem son koşulu sağlamadığından bir daire denklemi değildir .
Denklem son koşulu sağlamadığından bir daire denklemi değildir .
Alıştırma 4
Aşağıdaki üç noktadan geçen dairenin denklemini belirleyin:
![]()
Herhangi bir dairenin genel denklemi:
![]()
Bu nedenle parametreleri bulmak için noktaların koordinatlarını daire denkleminde yerine koymamız gerekir.
![]()
![]()
Ve
![]()
İlk nokta ile katsayıyı buluyoruz
![]()
![]()
İkinci nokta ile katsayıyı buluyoruz
![]()
![Rendered by QuickLaTeX.com \begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png)
Ve üçüncü noktadan katsayıyı buluyoruz
![]()
![Rendered by QuickLaTeX.com \begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png)
Sonuç olarak, çevrenin genel denklemi şöyledir:
![]()
Alıştırma 5
Bir dairenin zıt uçları aşağıdaki iki nokta ise:
![]()
Çemberin olağan denklemi nedir?
Eğer iki nokta çemberin uçları ise, merkezi bu iki noktanın orta noktası olacaktır:
![]()
![]()
![]()
Öte yandan, dairenin çapı iki nokta arasındaki mesafe olacaktır ve bu mesafe, iki noktanın oluşturduğu vektörün büyüklüğü kullanılarak hesaplanabilir:
![]()
![]()
Ve dairenin yarıçapı çapın yarısı kadardır:
![]()
Bu nedenle çemberin sıradan denklemi şu şekildedir:
![]()
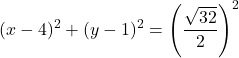
![]()
Son olarak bu makale işinize yaradıysa hiperbol (matematik) ve parabol (matematik) sayfalarımız da mutlaka ilginizi çekecektir. Hiperbol ve parabolün ne olduğu, denklemleri, özellikleri, örnekleri, çözümlü alıştırmalar hakkında detaylı anlatım bulacaksınız…