Kesişen çizgiler

Bu sayfada kesen doğrularla ilgili her şeyi bulacaksınız: ne anlama geldiklerini, farklı türlerini, iki doğrunun kesen olup olmadığını nasıl anlayacağınızı, ortak noktalarını nasıl bulacağınızı,… Ayrıca birkaç örnek ve çözülmüş alıştırmaları da görebileceksiniz. sekant çizgilerinden oluşur.

Kesişen iki çizgi nedir?

Matematikte sekant doğrularının tanımı şu şekildedir:

İki doğru yalnızca bir noktada kesiştiğinde kesişir. Bu nedenle kesişen doğruların tek bir ortak noktası vardır. Ayrıca, kesişen iki çizginin mutlaka aynı Kartezyen düzlemde bulunması gerekir.

İki doğrunun tek bir noktada kesişmesi kavramı önemlidir, çünkü eğer birden fazla kesişme noktası olsaydı bunlar çakışan doğrular olurdu, diğer taraftan kesişme noktaları olmasaydı paralel doğrular olurdu.

Kesişen çizgi örnekleri

Kesişen iki doğrunun anlamını gördükten sonra şimdi bu tip doğruların 2 farklı örneğine bakalım:

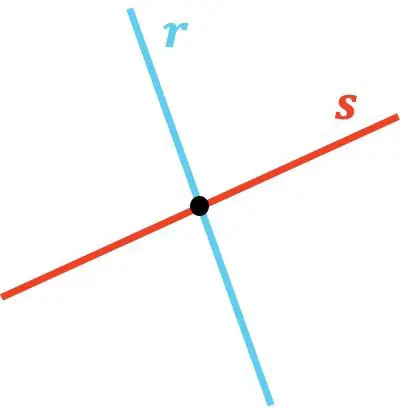
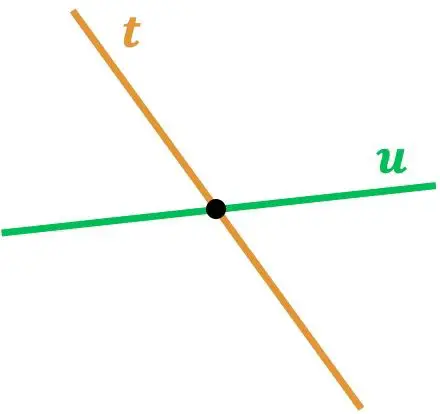
Gördüğünüz gibi r ve s doğruları kesişiyor çünkü bir noktada temas ediyorlar. Ve aynı şekilde t doğrusu da u doğrusuyla kesişiyor, çünkü bunların kesiştiği bir nokta var.

Kesişen çizgi türleri

İki tür kesişen çizgi vardır:

Dik çizgiler : 90° dik açıyla kesişen çizgilerdir.
Eğik çizgiler: 0° ile 90° arasında dar bir açıyla kesişen çizgilerden oluşur (dahil değildir).

Dik düz çizgiler

Dik çizgiler, dört adet 90 derecelik açı oluşturacak şekilde kesişen çizgilerdir.

Benzer şekilde, iki dik çizginin eğimleri her zaman aşağıdaki koşulu sağlar:

$m_r = -\cfrac{1}{m_s}$

Dik kesişen çizgilerin bir diğer özelliği, yön vektörleri (bir çizginin yönünü gösteren bir vektör) arasındaki nokta çarpımın sıfıra eşit olmasıdır.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Daha çok dik çizgilerle ilgileniyorsanız, bu bağlantıda dik çizgi örneklerini görebilirsiniz. Ek olarak, diğerine dik bir doğrunun nasıl hesaplanacağını, bu tür doğrunun özelliklerini, adım adım çözülen alıştırmaları vb. de bulacaksınız.

eğik çizgiler

Eğik çizgiler, çiftler halinde dar açılar ve geniş açılar oluşturacak şekilde kesişen çizgilerdir. Yani iki dar açı (90 dereceden küçük) ve iki geniş açı (90 dereceden büyük) yapın. Ancak iki doğrunun açısının tanımına göre iki doğru arasındaki açı, oluşturduğu açılardan en küçüğüdür.

İki eğik çizginin eğimleriyle arasındaki açı aşağıdaki formül kullanılarak hesaplanabilir:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

İki çizginin kesişip kesişmediğini nasıl anlarsınız?

İki çizginin göreceli konumunu bulmanın başlıca 3 yöntemi vardır:

İki çizginin yön vektörleri ile.
İki çizginin eğimleriyle.
İki çizginin örtülü (veya genel) denklemiyle.

Daha sonra iki doğrunun kesiştiğini bilmek için mevcut 3 yöntemin açıklamasını göreceğiz.

Çizgilerin yön vektörlerinden

İki farklı doğrunun yön vektörlerinin (bir doğrunun yönünü gösteren vektör) koordinatları orantılı değilse bu iki doğru kesişir.

Kesişen iki çizginin adım adım çözüldüğü bir alıştırmayı görelim:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Her iki çizgi de parametrik denklemler olarak ifade edilir, dolayısıyla her satırın yön vektörünün bileşenleri parametrenin önündeki sayılardır.

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Dolayısıyla yön vektörlerinin orantılı olup olmadığını görmek için koordinatlarını aralarında bölmemiz gerekir. Her iki bölmede de aynı sonucu alırsak orantılı olacaktır; Öte yandan sonucun farklı olması, vektörlerin orantılı olmadığı anlamına gelecektir.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

Bileşenlerin bölümleri eşdeğer olmadığından vektörler orantılı değildir ve dolayısıyla çizgiler kesişir.

yokuşların başlangıcında

İki doğrunun eğimleri farklıysa bu, doğruların kesiştiği anlamına gelir.

Örneğin aşağıdaki iki doğru eğimleri farklı olduğu için kesişiyor:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

Çizginin eğimi

$r$

-2 ve çizginin eğimi

$s$

3’tür.

$m_r =-2 \neq m_s =3$

İki doğru aynı eğime sahip olmadığından kesişirler.

Doğrunun örtülü denkleminden

İki doğrunun kesişip kesişmediği de doğruların örtülü denklemleri (veya genel denklemleri) aracılığıyla bulunabilir. Doğrunun örtülü denklemi aşağıdaki gibidir:

$Ax+By+C=0$

Dolayısıyla A ve B katsayıları orantılı olmadığında iki doğru kesişiyor.

Örtülü denklemleriyle tanımlanan kesişen iki doğrunun bir örneğini görelim:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Bunların kesişen iki çizgi olduğunu doğrulamak için A katsayısının (değişkenin önündeki sayı) orantılılığını analiz etmeliyiz.

$x$

) B katsayısı ile (değişkenin önündeki rakam)

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

İki terim orantılı değildir, dolayısıyla iki çizgi etkili bir şekilde kesişir.

Kesişen iki doğrunun ortak noktasını bulun

Görüldüğü gibi kesişen doğruların tek bir ortak noktası vardır. Bu nedenle iki kesen doğrunun kesişme noktasını hesaplamak için iki doğrunun oluşturduğu denklem sistemini çözmek gerekir.

Örnek olarak aşağıdaki iki doğrunun kesişme noktasını bulacağız:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

İki doğrunun kesişme noktasını belirlemek için iki doğrunun oluşturduğu doğrusal denklem sistemini çözmeliyiz:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

Bu durumda sistemi ikame yöntemiyle çözeceğiz. Bu nedenle değişkeni izole edeceğiz

$x$

birinci denklemden alıp ikinci denklemde yerine koyalım:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

Ve bilinmeyenin ne kadar değerli olduğunu bildiğimizde

$y$

Değerini aşağıdaki ifadenin yerine koyarız:

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

Bu nedenle denklem sisteminin çözümü iki doğrunun kesişme noktasıdır. Ve bu nokta

$\bm{(3,1)}.$

bir daireyi kesen çizgi

Normalde iki doğrunun kesiştiğini söylediğimizde az önce gördüğümüz kavramdan bahsediyoruz. Ancak geometride sekant çizgisinin başka bir anlamı daha vardır:

Bir daire ile kesişen bir çizgi, bir daireyi (veya bir eğriyi) iki farklı noktada kesen bir çizgidir.

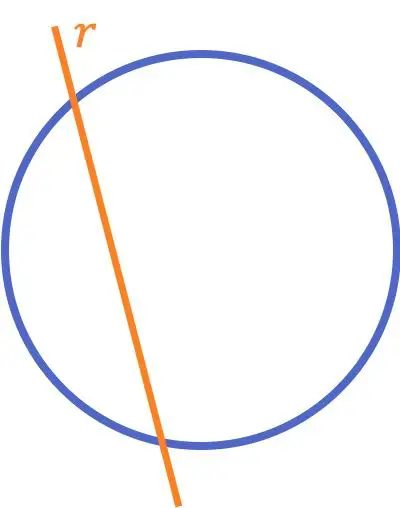
Genellikle ilkokulda öğretilen kesişen iki çizgi kavramından farklı olarak, bir daire ile kesişen bir çizginin bu tanımı, daha sonraki derslerde, daireli doğruların tüm göreceli konumlarıyla birlikte sıklıkla incelenir.