Denklem noktası – doğrunun eğimi

Bu sayfada doğrunun nokta-eğim denkleminin formülünü ve ayrıca bunu hesaplamanın farklı yollarını bulacaksınız. Ayrıca çeşitli örnekleri görebilecek ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Doğrunun nokta-eğim denklemi formülü

Bir çizginin nokta-eğim denklemi, bir çizgiyi matematiksel olarak ifade etmenin bir yoludur. Özellikle bir doğrunun nokta-eğim denklemini bulmak için sadece doğru üzerindeki bir noktanın eğimine ve koordinatlarına ihtiyacınız vardır.

Doğrunun nokta-eğim denkleminin formülü aşağıdaki gibidir:

$y-y_0=m(x-x_0)$

Altın

$m$

çizginin eğimi ve

$x_0, y_0$

doğru üzerindeki bir noktanın koordinatlarıdır

$P(x_0,y_0).$

Bir örnek kullanarak doğrunun nokta-eğim denkleminin nasıl hesaplandığını görelim:

noktasından geçen doğrunun nokta-eğim denklemini yazınız.
$P(2,-1)$

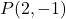
ve eğim m=3.

Doğrunun nokta-eğim denkleminin formülü aşağıdaki gibidir:

$y-y_0=m(x-x_0)$

Bu durumda ifade bize doğrunun eğiminin m=3 olduğunu söylüyor, dolayısıyla doğrunun denklemi şu şekilde olacaktır:

$y-y_0=3(x-x_0)$

Ayrıca doğrunun bu noktadan geçtiğini de biliyoruz.

$P(2,-1)$

bu nedenle bu noktanın koordinatlarını denklemde yerine koymalıyız:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

Dolayısıyla çizginin nokta-eğim denklemi şu şekildedir:

$\bm{y+1=3(x-2)}$

Nokta-eğim denkleminin yanı sıra, bir çizgiyi analitik olarak ifade etmenin başka yollarının da olduğunu unutmayın: vektör denklemi, parametrik denklemler, sürekli denklem, örtülü denklem (veya genel) ve bir doğrunun açık denklemi. Daha fazla ilgileniyorsanız, her birinin ne olduğunu web sitemizden kontrol edebilirsiniz.

Bir çizginin eğimi ne anlama gelir?

Bir doğrunun nokta-eğim denkleminin tanımında gördüğümüz gibi, parametre

$m$

doğrunun eğimidir. Ama gerçekte… bir çizginin eğimi ne anlama geliyor? Bunu bir çizginin grafiksel gösteriminden görelim:

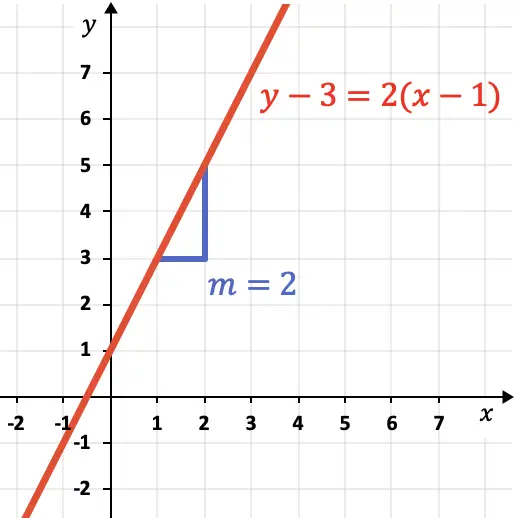
Çizginin eğimi onun dikliğini gösterir. Grafik çizgisinden görebileceğiniz gibi,

$m$

doğru 1 yatay birim için 2 dikey birim yükseldiği için 2’ye eşittir.

Açıkçası, eğim pozitifse fonksiyon artıyor (yukarı gidiyor), diğer taraftan eğim negatifse fonksiyon azalıyor (aşağı gidiyor).

Bir çizginin eğimi nasıl hesaplanır

Ayrıca bir doğrunun eğimini sayısal olarak belirlemenin 3 farklı yolu vardır:

Doğru üzerinde iki farklı nokta verildiğinde
$P_1(x_1,y_1)$

Ve

$P_2(x_2,y_2),$

Doğrunun eğimi şuna eşittir:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Evet
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

doğrunun yön vektörüdür, eğimi:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Evet
$\alpha$

apsis ekseni (X ekseni) ile doğrunun oluşturduğu açıdır, çizginin eğimi söz konusu açının tanjantına eşdeğerdir:

$m = \text{tg}(\alpha )$

Çizgilerin göreceli konumu

Son olarak, bir doğrunun eğimi aynı zamanda birkaç doğru arasındaki ilişkiyi bilmek için de kullanılır. İki paralel doğrunun eğimi aynı olduğundan ve bir doğrunun eğimi diğer doğrunun eğiminin negatif tersi ise bu iki doğrunun birbirine dik olduğu anlamına gelir.

İki noktadan geçen doğrunun nokta-eğim denklemini hesaplayın

Çok sık karşılaşılan bir problem, doğruya ait iki noktadan nokta-eğim denkleminin belirlenmesidir. Bir örnek üzerinden nasıl çözüldüğünü görelim:

Aşağıdaki iki noktadan geçen doğrunun nokta-eğim denklemini bulun:

$P_1(5,2) \qquad P_2(3,6)$

Doğrunun nokta-eğim denklemini bulmak için doğrunun eğiminin ne olduğunu bulmamız gerekir. Böylece çizginin eğimini iki nokta üst üste formülünü kullanarak hesaplıyoruz:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

Böylece çizginin nokta-eğim denklemi aşağıdaki gibi olacaktır:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Bu nedenle, doğru üzerindeki bir noktanın Kartezyen koordinatlarını denklemde yerine koymamız yeterlidir:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

İfadenin diğer noktasını doğrunun denklemine koyarsak da iyi olur:

$P_1(3,6)$

$y-6=-2(x-3)$

Grafikten bir doğrunun nokta-eğim denklemini bulun

Yukarıdaki bölümlerde gördüğümüz gibi bir doğrunun nokta-eğim denklemini sayısal olarak bulmanın birkaç yolu vardır. Ancak grafiksel olarak da bulunabilir. Bunun nasıl yapıldığını bir örnek üzerinden görelim:

Aşağıdaki grafikte gösterilen doğrunun nokta-eğim denklemini belirleyin:

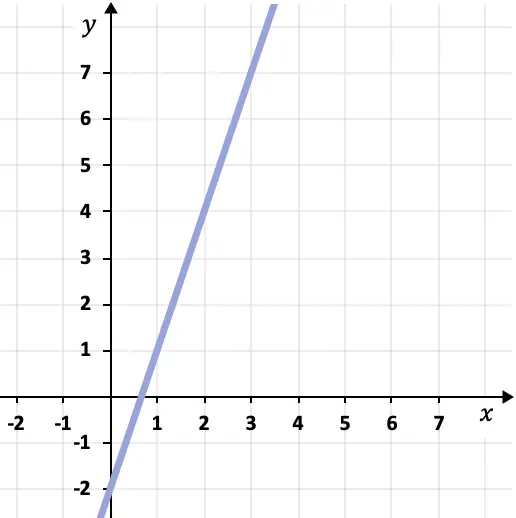
Çizilen çizginin nokta-eğim denklemini belirlemek için eğimini ve doğru üzerinde bir nokta bulmamız gerekir.

Bu durumda doğrunun eğimi 3’e eşittir çünkü doğru her yatay birim için 3 düşey birim yükselmektedir.

$m = 3$

Daha sonra çizgi üzerinde bir noktaya ihtiyacımız var. Bunu yapmak için grafikte çizginin geçtiği herhangi bir noktayı, örneğin (1,1) noktasını seçebiliriz.

$P(1,1)$

Dolayısıyla artık doğrunun nokta-eğim denklemini formülü uygulayarak bulabiliriz:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

Bir doğrunun denklem noktasının eğimini grafiksel olarak belirleme

Çözülmüş Nokta-Eğim Denklemi Problemleri

1. Egzersiz

noktasından geçen doğrunun nokta-eğim denklemini yazınız.

$P(1,4)$

ve eğimi

$m=-2.$

çözümü gör

Doğrunun nokta-eğim denkleminin formülü şöyledir:

$y-y_0=m(x-x_0)$

Bu durumda ifade bize doğrunun eğiminin m=-2 olduğunu söylüyor, dolayısıyla doğrunun denklemi şu şekilde olacaktır:

$y-y_0=-2(x-x_0)$

Ayrıca ifadeden doğrunun noktadan geçtiğini de biliyoruz.

$P(1,4)$

Bu nedenle noktanın koordinatlarını doğrunun denkleminde yerine koymak yeterlidir:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Alıştırma 2

Aşağıdaki iki noktadan geçen doğrunun nokta-eğim denklemi nedir?

$P_1(1,6) \qquad P_2(4,0)$

Çözüme bakın

Doğrunun nokta-eğim denklemini bulmak için doğrunun eğiminin ne olduğunu bulmamız gerekir. Bu nedenle doğrunun eğimini aşağıdaki formülle hesaplıyoruz:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

Böylece çizginin nokta-eğim denklemi aşağıdaki gibi olacaktır:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Bu nedenle denklemde yalnızca doğru üzerindeki bir noktanın koordinatlarını yerine koymamız gerekir:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Açıklamanın diğer noktasını da denkleme koymak doğru olurdu:

$y=-2(x-4)$

Alıştırma 3

Aşağıdaki iki noktadan geçen doğrunun nokta-eğim denklemini bulun:

$P_1(1,-2) \qquad P_2(2,3)$

Çözüme bakın

Doğrunun nokta-eğim denklemini bulmak için önce eğimini hesaplamanız gerekir:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

Böylece çizginin nokta-eğim denklemi aşağıdaki gibi olacaktır:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Bu nedenle denklemde yalnızca doğru üzerindeki bir noktanın koordinatlarını yerine koymamız gerekir:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Doğrunun denklemindeki ifadedeki diğer noktayı da koymak doğrudur:

$y-3=5(x-2)$

Alıştırma 4

X ekseni ile 45° açı oluşturan ve koordinat orijininden geçen doğrunun nokta-eğim denklemini hesaplayınız.

Çözüme bakın

Eğer çizgi OX ekseni ile 45 derecelik bir açı yaparsa eğimi şöyle olacaktır:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

Doğrunun eğimini bildiğimizde, doğru üzerindeki bir noktayı denklemin yerine koyarak nokta-eğim denklemini bulabiliriz. Ek olarak ifade bize doğrunun koordinat orijininden geçtiğini, yani (0,0) noktasından geçtiğini söyler. Henüz:

$P(0,0)$