Doğrunun açık denklemi

Bu sayfada bir doğrunun açık denklemi hakkında her şeyi bulacaksınız: nedir, formülü nedir, hesaplama örnekleri vb. Ayrıca eğimin ne anlama geldiğine ve açık denklemin kesim noktasına ilişkin ayrıntılı bir açıklama da bulacaksınız. Üstelik farklı örnekler görecek ve adım adım çözülen alıştırmalar ile pratik yapabileceksiniz.

Doğrunun açık denklemi nedir?

Bir çizginin matematiksel tanımının, eğriler veya açılar olmadan aynı yönde temsil edilen ardışık noktalar kümesi olduğunu unutmayın.

Dolayısıyla açık çizgi denklemi, herhangi bir doğruyu matematiksel olarak ifade etmenin bir yoludur. Bunun için doğrunun eğimini ve Y ekseniyle kesiştiği noktayı bilmeniz yeterli.

Doğrunun açık denklemi için formül

Doğrunun açık denkleminin formülü şöyledir:

$y=mx+n$

Altın

$m$

çizginin eğimi ve

$n$

y-kesme noktası, yani Y ekseniyle kesiştiği yükseklik.

Doğrunun açık denkleminin nasıl hesaplandığını bir örnek üzerinden görelim:

noktasından geçen doğrunun açık denklemini yazınız.
$P(3,1)$

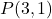
ve eğim m=2.

Doğrunun açık denkleminin formülü şöyledir:

$y= mx+n$

Bu durumda ifade bize doğrunun eğiminin m=2 olduğunu söylüyor, dolayısıyla doğrunun denklemi şu şekilde olacaktır:

$y= 2x+n$

Bu nedenle n katsayısını hesaplamak yeterlidir. Bunu yapmak için doğruya ait bir noktayı denklemde yerine koymalıyız. Bu durumda ifade bize doğrunun noktadan geçtiğini söyler.

$P(3,1),$

Henüz:

$P(3,1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=1} \ 1=2\cdot 3 +n$

Ve n’nin değerini bulmak için ortaya çıkan denklemi çözüyoruz:

$1=2\cdot 3 +n$

$1=6 +n$

$1-6=n$

$-5 = n$

Bu nedenle doğrunun açık denklemi şu şekildedir:

$\bm{y= 2x-5}$

Açık denklemin yanı sıra, bir doğruyu analitik olarak ifade etmenin başka yollarının da olduğunu unutmayın. Örneğin, yön vektörünün ve doğru üzerindeki bir noktanın kendi koordinatlarıyla ifade edilmesi nedeniyle diğerlerinden farklı bir çizgi denklemi türü olan vektör denklemi . Bağlantıda ne olduğunu ve neden bu kadar özel olduğunu görebilirsiniz.

m ve n parametrelerinin anlamı

Doğrunun açık denkleminin tanımında gördüğümüz gibi, parametre

$m$

çizginin eğimi ve

$n$

y-kesme noktası. Peki bu ne anlama geliyor? Bunu bir çizginin grafiksel gösteriminden görelim:

Bağımsız terimi

$\bm{n}$

doğrunun bilgisayar ekseni (OY ekseni) ile kesiştiği noktadır . Yukarıdaki grafikte

$n$

1’e eşittir çünkü doğru y eksenini y=1’de keser.

Öte yandan terim

$\bm{m}$

doğrunun eğimini yani eğimini gösterir . Grafikte gördüğünüz gibi,

$m$

doğru 1 yatay birim için 2 dikey birim yükseldiği için 2’ye eşittir.

Açıkçası, eğim pozitifse fonksiyon artıyor (yukarı gidiyor), diğer taraftan eğim negatifse fonksiyon azalıyor (aşağı gidiyor).

Bir çizginin eğimini hesaplayın

Ayrıca bir doğrunun eğimini sayısal olarak belirlemenin 3 farklı yolu vardır:

Doğru üzerinde iki farklı nokta verildiğinde
$P_1(x_1,y_1)$

Ve

$P_2(x_2,y_2),$

Doğrunun eğimi şuna eşittir:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Evet
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

doğrunun yön vektörüdür, eğimi:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Evet
$\alpha$

apsis ekseni (X ekseni) ile doğrunun oluşturduğu açıdır, çizginin eğimi söz konusu açının tanjantına eşdeğerdir:

$m = \text{tg}(\alpha )$

Çizgilerin göreceli konumu

Son olarak, bir doğrunun eğimi aynı zamanda birkaç doğru arasındaki ilişkiyi bilmek için de kullanılır. İki paralel doğrunun eğimi aynı olduğundan ve bir doğrunun eğimi diğer doğrunun eğiminin negatif tersi ise bu iki doğrunun birbirine dik olduğu anlamına gelir.

İki noktadan geçen doğrunun açık denklemini hesaplayın

Çok tipik bir problem, içinden geçtiği iki nokta verilen bir doğrunun açık denklemini bulmaktır. Bir örnek üzerinden nasıl çözüldüğünü görelim:

Aşağıdaki iki noktadan geçen doğrunun açık denklemini belirleyin:

$P_1(4,-1) \qquad P_2(2,5)$

Doğrunun açık denklemini bulmak için m ve n parametrelerinin değerinin ne olduğunu bilmeniz gerekir. Bu yüzden önce iki nokta üst üste formülünü kullanarak doğrunun eğimini hesaplıyoruz:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{5-(-1)}{2-4} = \cfrac{6}{-2}= -3$

$y=-3x+n$

Daha sonra denklemde doğru üzerindeki bir noktayı değiştirerek y kesme noktasını bulabiliriz:

$P_1(4,-1)$

$y= -3x+n \ \xrightarrow{x=4 \ ; \ y=-1} \ -1=-3\cdot 4 +n$

$-1 =-12+ n$

$-1 +12= n$

$11= n$

Dolayısıyla doğrunun açık denklemi şöyledir:

$\bm{y=-3x+11}$

Örtülü denklemden açık denklemi bulma

Son olarak, sıklıkla karşılaştığımız bir başka problem türü, doğrunun açık denklemini örtülü denkleminden (genel veya Kartezyen denklem olarak da bilinir) bulmaktır. Açıkçası, aşağıdaki yöntemi anlamak için ima edilen denklemin tam olarak ne olduğunu ve nasıl olduğunu bilmeniz gerekir; ama eğer hiç hatırlamıyorsanız linkten inceleyebilirsiniz.

Dolayısıyla, bir doğrunun örtülü (veya genel) denklemine zaten hakimseniz, bu prosedürün nasıl çalıştığını görelim:

Aşağıdaki doğrunun açık denklemini bulun:

$3x-2y+8 =0$

Doğrunun açık denklemini bulmak için yapmamız gereken tek şey değişkeni çözmektir.

$\bm{y}.$

Yani şartları olmadan aktarıyoruz

$y$

denklemin diğer tarafında:

$-2y=-3x-8$

Şimdi değişkeni temizliyoruz

$y:$

$\displaystyle y=\frac{-3x-8}{-2}$

Ve son olarak basitleştiriyoruz:

$\displaystyle y=\frac{-3x}{-2} -\cfrac{8}{-2}$

$\displaystyle y=\frac{3x}{2} -(-4)$

$\displaystyle \bm{y=}\frac{\bm{3}}{\bm{2}}\bm{x +4}$

Bu nedenle bu doğrunun eğimi

$\displaystyle \frac{3}{2}$

ve y-kesme noktası 4’tür.

Çözülmüş Açık Denklem Problemleri

1. Egzersiz

Aşağıdaki doğruların eğimini ve y kesim noktasını belirtin:

$\begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}$

Çözüme bakın

Bir çizginin açık denklemi aşağıdaki formülü takip eder:

$y=mx+n$

Altın

$m$

eğim ve

$n$

başlangıç noktasındaki bilgisayar. Henüz:

$\bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}$

$\bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}$

$\bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}$

Son satır örtülü denklemiyle ifade edilir, bu yüzden önce onu açık bir denkleme aktarmamız gerekir (çözün

$y$

) o zaman parametreleri tanımlayabiliriz:

$\bm{D)} \ 4x+2y-6=0$

$2y =-4x+6$

$y =\cfrac{-4x+6}{2}$

$y =-2x+3$

$\begin{cases} m = -2 \\[2ex] n=3 \end{cases}$

Alıştırma 2

Noktadan geçen doğrunun açık denklemini bulun

$P(2,-3)$

ve eğimi var

$m=-2.$

Çözüme bakın

Doğrunun açık denkleminin formülü şöyledir:

$y= mx+n$

Bu durumda doğrunun eğimi -2 olmalıdır, dolayısıyla doğrunun denklemi aşağıdaki forma sahip olacaktır:

$y= -2x+n$

Bu nedenle n katsayısını hesaplamak yeterlidir. Bunu yapmak için, doğruya ait bir noktayı denkleminde yerine koymalı ve ortaya çıkan denklemi çözmelisiniz:

$P(2,-3)$

$y= -2x+n \ \xrightarrow{x=2 \ ; \ y=-3} \ -3=-2\cdot 2 +n$

$-3=-4 +n$

$-3+4= n$

$1= n$

Kısaca doğrunun açık denklemi şöyledir:

$\bm{y= -2x+1}$

Alıştırma 3

Aşağıdaki iki noktadan geçen doğrunun açık denklemini bulun:

$P_1(6,-1) \qquad P_2(3,2)$

Çözüme bakın

Doğrunun açık denklemini bulmak için m ve n parametrelerinin değerinin ne olduğunu bilmeniz gerekir. Bu nedenle önce iki noktanın koordinatlarından doğrunun eğimini hesaplıyoruz:

$m = \cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{2-(-1)}{3-6} = \cfrac{3}{-3}= -1$

$y=-x+n$

Daha sonra denklemde doğru üzerindeki bir noktayı değiştirerek kesişme noktasını belirleriz:

$P_1(6,-1)$

$y= -x+n \ \xrightarrow{x=6 \ ; \ y=-1} \ -1=-6 +n$

$-1 +6= n$

$5= n$

Dolayısıyla doğrunun açık denklemi şöyledir:

$\bm{y=-x+5}$

Alıştırma 4

X ekseni ile 45° açı yapan ve koordinatların orijininden geçen doğrunun açık denklemini hesaplayınız.

Çözüme bakın

Eğer çizgi OX ekseni ile 45 derecelik bir açı yaparsa eğimi şöyle olacaktır:

$m = \text{tg}(45º) = 1$

$y=x+n$

Doğrunun eğimini bildiğimizde, denklemde doğrunun üzerindeki bir noktayı değiştirerek y kesme noktasını hesaplayabiliriz. Ek olarak ifade bize doğrunun koordinat orijininden geçtiğini, yani (0,0) noktasından geçtiğini söyler. Henüz:

$P(0,0)$