Paralelkenar kuralı veya yasası

Bu sayfada paralelkenar kuralının (veya yasasının) açıklamasını bulacaksınız. Ek olarak, paralelkenar kuralını kullanan çeşitli vektör toplama ve çıkarma örneklerinin yanı sıra gerçek dünyadaki uygulamaları da göreceksiniz.

Paralelkenar kuralı nedir?

Bildiğiniz gibi vektörel büyüklükler gerçek sayılarla aynı şekilde eklenemez veya çıkarılamaz çünkü bunların 2 bileşeni (R2’de) veya 3 bileşeni (R3’te) vardır ve vektörlerin yönleri farklı olabilir. Bu nedenle vektör işlemlerini gerçekleştirmek için aşağıdakilerden oluşan paralelkenar kuralı gibi başka yöntemlere ihtiyaç vardır:

Matematikte paralelkenar kuralı , iki vektörün grafiksel gösterimlerine eklenmesi veya çıkarılması için kullanılan bir prosedürdür.

Paralelkenar yöntemi kesinlikle vektörlerin toplanmasında ve çıkarılmasında (grafiksel olarak) en çok kullanılan yöntemdir çünkü kullanımı çok kolay bir tekniktir. Örneğin fizikte kuvvetleri toplamak ve çıkarmak için kullanılır.

Öte yandan kural, vektörleri eklemek veya çıkarmak isteyip istemediğimize bağlı olarak biraz değişir, bu nedenle aşağıda her iki versiyonu da ayrı ayrı açıklayacağız.

İki vektörün eklenmesi için paralelkenar kuralı

İki vektörü grafiksel olarak eklemek istiyorsak paralelkenar kuralını veya yasasını uygulama adımları şunlardır:

1. Öncelikle vektörleri çizip aynı uygulama noktasına konumlandırıyoruz, yani her iki vektörün orijinlerini aynı noktaya yerleştiriyoruz.
2. Daha sonra bir vektörün sonuna diğer vektöre paralel bir çizgi çizeriz. Ve adımı diğer vektörle tekrarlıyoruz. Bu nedenle bir paralelkenarın çizimini elde edeceğiz (kuralın adı da buradan gelmektedir).
3. Son olarak toplamdan elde edilen vektör, vektörlerin ortak orijininden iki paralel çizginin kesişme noktasına kadar uzanan paralelkenarın köşegeni olacaktır.

Aşağıdaki genel örnekte paralelkenar kuralının nasıl kullanıldığını görebilirsiniz:

Paralelkenar kuralıyla pratik yapmak istiyorsanız, aşağıdaki bağlantıda daha fazla örnek ve çeşitli çözülmüş vektör toplama alıştırmalarına başvurabilirsiniz. Bu sayfada ayrıca vektörleri grafiksel olarak eklemenin diğer yöntemlerini ve hatta bunların sayısal olarak nasıl ekleneceğini de bulacaksınız.

İki vektörün çıkarılması için paralelkenar kuralı

Paralelkenar kuralı veya yöntemi aynı zamanda bir grafikten iki vektörü çıkarmak için de kullanılır. Yani, vektör çıkarma adımları şunlardır:

1. Öncelikle iki vektörü grafikte temsil edip aynı uygulama noktasına konumlandırıyoruz, yani her iki vektörün orijinlerini aynı noktaya yerleştiriyoruz.
2. İkinci olarak işlemde çıkarılan vektörün zıt vektörünü çiziyoruz, yani çıkarma yapan vektörü ters çeviriyoruz.
3. Daha sonra vektörün sonundaki işaret değişim vektörüne paralel bir çizgi çizerek toplamı . Ve işlemi diğer vektörle tekrarlıyoruz. Böylece bir paralelkenarın çizimini elde edeceğiz (dolayısıyla kuralın adı).
4. Son olarak çıkarma işleminin sonucu, iki vektörün ortak orijininden iki paralel çizginin kesiştiği noktaya giden vektör olacaktır.

İki vektörün paralelkenar yasasıyla çıkarıldığı aşağıdaki genel örneğe bakın:

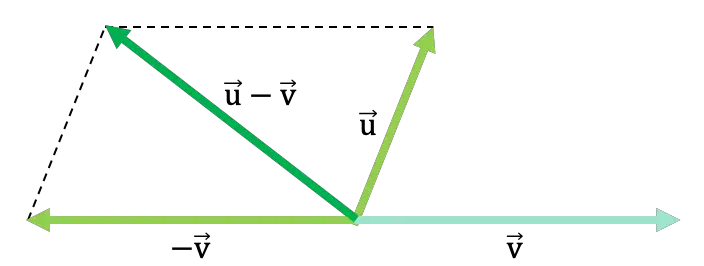
Aşağıdaki bağlantıda paralelkenar kuralıyla vektör çıkarma işleminin daha fazla örneğini görebilir, ayrıca çözülmüş vektör çıkarma alıştırmalarıyla pratik yapabilirsiniz. Ek olarak, vektörleri grafiklerinden çıkarmak için başka teknikler ve son olarak bunların sayısal olarak nasıl çıkarıldığını bulacaksınız.

Son olarak, eğer bu tekniğin açıklaması sizin için yararlı olduysa, sağ el kuralının ne olduğunu bilmek de mutlaka ilginizi çekecektir. Bağlantı sayfasında bunun ne olduğunu, hangi vektör işlemi için kullanıldığını ve bu kuralın mevcut farklı varyasyonlarını görebilirsiniz.