Bu sayfada bir vektörün bileşenlerinin (veya koordinatlarının) ne olduğuna dair açıklama bulacaksınız. Ayrıca iki noktadan nasıl hesaplandıklarını, hatta modülleri ve açıları üzerinden nasıl ayrıştırıldıklarını görebileceksiniz. Ayrıca adım adım çözülen örnekler ve alıştırmalar bulacaksınız.
Bir vektörün bileşenleri nelerdir?
Bir vektörün bileşenleri, bir vektörün Kartezyen eksenlere izdüşümleridir. Dolayısıyla vektörün x eksenine izdüşümü vektörün X bileşenidir ve benzer şekilde vektörün y eksenine izdüşümü de vektörün Y bileşenidir.
Bir vektörün bileşenleri aynı zamanda bir vektörün koordinatları olarak da adlandırılabilir.
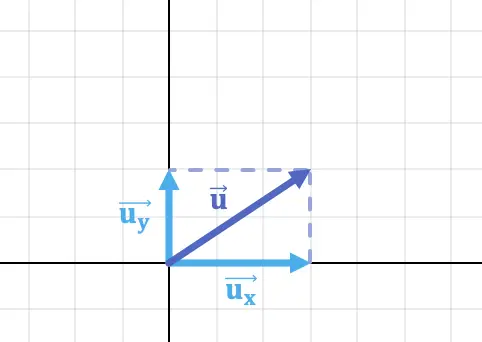
Örneğin yukarıdaki görseldeki vektörün yatay bileşeni ve dikey bileşeni şöyledir:
![]()
![]()
Yani vektör:
![]()
Dolayısıyla bir vektörün bileşenleri, bir vektörün koordinat sistemindeki temsili olarak da tanımlanabilir. Açıkçası, eğer iki boyutlu bir sistemse (r2’de) vektör iki bileşene sahip olacaktır; diğer taraftan, eğer üç boyutlu bir tabansa (r3’te) vektör üç bileşenden oluşacaktır.
Bir vektörün Kartezyen bileşenleri çok önemlidir çünkü bunlarla vektörün esas olarak yönü, yönü ve modülü (veya büyüklüğü) olan özelliklerini bilebiliriz. Ayrıca vektör işlemlerini gerçekleştirmek için de kullanılırlar.
Bir vektörün bileşenleri iki noktadan nasıl hesaplanır
Bir vektörün koordinatlarını grafiksel olarak nasıl bulacağımızı gördük, ancak bileşenlerini sayısal olarak da belirleyebiliyoruz.
Bir vektörün bileşenlerini sayısal olarak hesaplamak için iki noktayı bilmemiz gerekir: onun kökenini ve sonunu, başka bir deyişle nerede başlayıp nerede bittiğini. Çünkü bir vektörün bileşenleri, onun ucundan kökeninin çıkarılmasıyla elde ettiğimiz koordinatlardır.
![]()
Örneğin, kökeni A(3,1) noktası ve sonu B(5,4) noktası olan vektörü hesaplayacağız:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4c740536015a29149532a4a1eb46f4f7_l3.png)
Gördüğünüz gibi bir vektörün bileşenlerini belirlemek çok zor değil ancak oldukça önemlidir. Örneğin, en yaygın kullanılan vektör türlerinden biri dik (veya dik) vektörlerdir; Bir vektörün koordinatlarının ne olduğunu anlarsanız dik vektörleri hesaplamak çok kolaydır. Dik vektörlerin açıklamasında bunun nasıl yapıldığını görebilirsiniz.
Bir vektörün bileşenleri modülünden ve açısından nasıl hesaplanır?
Bir vektörün bileşenlerini büyüklüğünden ve X ekseniyle yaptığı açıdan da bulabilirsiniz. Bu işleme vektör ayrıştırması denir.
Böylece vektörün X ve Y bileşenleri kosinüs ve sinüsün trigonometrik oranlarıyla hesaplanabilir:

Resimde görebileceğiniz gibi, bir vektörün modülü ve bileşenleri bir dik üçgeni tamamlar, böylece trigonometrinin temel formülleri uygulanabilir.
Bir vektörün modülünün nasıl hesaplandığını hatırlamıyorsanız, bir vektörün modülünün ne olduğuna bakabilirsiniz. Burada bir vektörün büyüklüğüne ilişkin formülün yanı sıra örnekler, adım adım çözülmüş alıştırmalar ve bir vektörün büyüklüğünün tüm özelliklerini bulacaksınız. Bu çok eksiksiz bir açıklamadır, böylece onu mükemmel bir şekilde anlayacaksınız. ✅
Her zaman pozitif olan bir vektörün büyüklüğünden farklı olarak, sinüs ve kosinüs negatif değerler alabileceği için bileşenleri negatif olabilir.
Örnek olarak modülü ve OX ekseniyle açısı olan vektörün vektör ayrıştırmasını yapacağız:
![]()
Vektörün X bileşeni, modülün açının kosinüsüyle çarpımına eşittir:
![]()
Ve vektörün Y bileşeni, modülün çarpımına ve açının sinüsüne eşittir:
![]()
Yani vektörün koordinatları:
![]()