Bir vektörün bir sayı ile çarpımı

Bu sayfada bir vektörün bir gerçek sayıyla (veya bir skalerle) sayısal ve grafiksel olarak nasıl çarpılacağı açıklanmaktadır. Ayrıca bir vektörün skaler çarpımı ile ilgili örnekler ve çözülmüş alıştırmalar da bulacaksınız. Son olarak vektörlerle yapılan bu tip işlemin özellikleri de anlatılmıştır.

Bir vektörü gerçek sayıyla nasıl çarparsınız?

Bir vektör ile bir sayının (veya bir skalerin) çarpımını sayısal olarak hesaplamak için, vektörün her bir bileşeninin sayı ile çarpılması gerekir.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

$k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y)$

Böylece, bir vektörün bir sayı ile çarpılması sonucu aşağıdaki özelliklere sahip yeni bir vektör elde edilir:

Bir vektörün bir skalerle çarpımının sonucu, orijinal vektörle aynı yönde yeni bir vektör üretir.
Ayrıca sayı pozitifse yeni vektör aynı yöne sahip olacaktır.
Veya sayı negatifse tam tersi bir anlam taşıyacaktır.
Ortaya çıkan vektörün büyüklüğü, orijinal vektörün büyüklüğünün skalerle çarpımına eşittir.

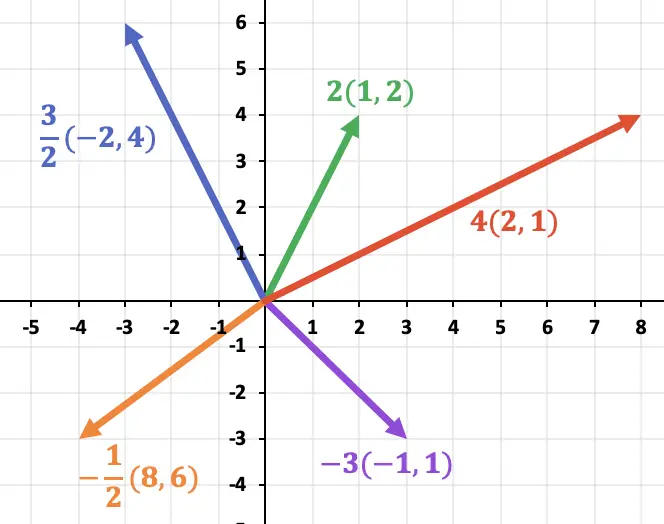
Aşağıdaki grafikte skalerin işaretine bakılmaksızın vektörün yönünün nasıl korunduğunu görebilirsiniz. Öte yandan vektörün yönü çarptığı sayının işaretine bağlıdır.

bir sayının veya skalerin bir vektörle çarpımı veya çarpımı

Ayrıca aşağıdaki grafikte, ortaya çıkan çarpım vektörünün büyüklüğünün, orijinal vektörün büyüklüğünün skalerle çarpımına eşit olduğu açıkça görülmektedir.

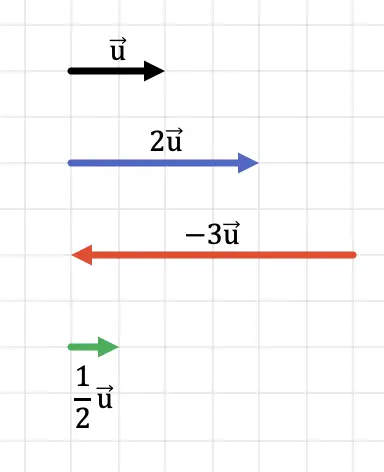
Bir sayının bir vektörle çarpımının veya çarpımının modülü nasıl gelişir?

Açıkçası, eğer vektörü 1’den büyük bir sayı ile çarparsak, sonuç daha büyük uzunlukta (daha büyük modüllü) bir vektör olur. Öte yandan, vektörü 1’den küçük bir sayıyla çarparsak sonuç daha kısa uzunlukta (daha küçük modül) bir vektör olur.

Not: Bir vektör ile bir skalerin çarpımını , vektörlerin nokta çarpımı ile karıştırmayın. İsimleri benzer olmasına rağmen tamamen farklı iki kavramdır.

Bir vektörün skaler çarpımı örneği

Daha sonra, bir vektör ile bir sayının çarpımının nasıl hesaplandığına dair sayısal bir örnek göreceğiz:

Aşağıdaki vektörü 4 ile çarpın:

$\vv{\text{u}} =(2,-3)$

$4\cdot \vv{\text{u}} =(4 \cdot 2 \ , \ 4 \cdot (-3)) = \bm{(8,-12)}$

Gördüğünüz gibi bu tür vektör işlemleri çok karmaşık değil çünkü çok fazla hesaplama yapmanıza gerek yok.

Ancak vektör toplama ve vektör çıkarma gibi daha karmaşık vektör işlemleri de vardır. Bir vektör ile bir skalerin çarpımının nasıl hesaplanacağını zaten anladıysanız, bir sonraki seviyeye geçmenizi ve vektör toplama ve vektör çıkarma işlemlerini nasıl çözeceğinizi görmenizi öneririz çünkü bunlar biraz daha zor işlemlerdir ve aslında çok daha fazla kullanılıyorlar (daha önemliler).

Bir vektörü bir sayıyla çarpmanın özellikleri

Bir vektör ile bir sayının çarpımı aşağıdaki özelliklere sahiptir:

İlişkisel özellik : Vektör birden fazla sayıyla çarpıldığında çarpmaların sırası önemli değildir.

$k \cdot (k' \cdot \vv{\text{u}}) =(k\cdot k') \cdot \vv{\text{u}}$

Vektörlerin toplanması ve çıkarılmasına göre dağılma özelliği :

$k \cdot (\vv{\text{u}}+ \vv{\text{v}})=k\cdot \vv{\text{u}} + k\cdot \vv{\text{v}}$

$k \cdot (\vv{\text{u}}- \vv{\text{v}})=k\cdot \vv{\text{u}} - k\cdot \vv{\text{v}}$

Skalerlerin toplamına göre dağılım özelliği :

$(k+k') \cdot \vv{\text{u}} =k\cdot \vv{\text{u}} + k'\cdot \vv{\text{u}}$

Nötr eleman : Açıkçası, herhangi bir vektörün 1 ile çarpılması, vektörün kendisini verir:

$1\cdot \vv{\text{u}} = \vv{\text{u}}$

Bir vektörün bir skalerle çarpımına ilişkin çözülmüş problemler

1. Egzersiz

Aşağıdaki vektörün çarpımının sonucunu 3 ile analitik olarak hesaplayın:

$\vv{a}=(-2,5)$

Çözüme bakın

Çarpımı bulmak için vektörün her koordinatını 3 ile çarpmanız gerekir:

$3\cdot \vv{a}=(3\cdot (-2), 3 \cdot 5) = \bm{(-6,15)}$

Alıştırma 2

Aşağıdaki vektörü 6 ile çarpın ve modülünü bulun:

$\vv{a}=(3,-4)$

Çözüme bakın

Önce vektörü skalerle çarpıyoruz:

$6\cdot \vv{a}=(6\cdot 3, 6 \cdot (-4)) = (18,-24)$

Artık elde edilen vektörün büyüklüğünü hesaplamanın iki yolu vardır. Birincisi, orijinal vektörün büyüklüğünü bulmak ve ardından bunu 6 ile çarpmak:

$\lvert \vv{a} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{25} =5$

$6\cdot \lvert \vv{a} \rvert =6\cdot 5 =\bm{30}$

İkinci yol ise çarpmada elde edilen vektörün büyüklüğünü doğrudan hesaplamaktır:

$\lvert 6\cdot \vv{a} \rvert =\sqrt{18^2+(-24)^2} = \sqrt{900} =\bm{30}$

Böylece her iki prosedürde de sonucun modülün hesaplandığı yönteme bağlı olmadığı gösterilmiştir.

Alıştırma 3

Aşağıdaki vektörden:

$\vv{a}=(4,-1)$

Aşağıdaki işlemleri cebirsel olarak hesaplayın:

$2\cdot \vv{a}$

$-3\cdot \vv{a}$

$\displaystyle \frac{1}{2} \cdot \vv{a}$

$4\cdot \vv{a}$

Daha sonra, ortaya çıkan vektörlerin orijinal vektörle aynı yön ve yöne sahip olup olmadığını belirleyin ve bunları en kısadan en uzuna doğru sıralayın.

Çözüme bakın

İlk önce çarpımları hesaplıyoruz:

$2\cdot \vv{a}=(2\cdot 4, 2 \cdot (-1)) = (8,-2)$

$-3\cdot \vv{a}=(-3\cdot 4, -3 \cdot (-1)) = (-12,3)$

$\displaystyle \frac{1}{2}\cdot \vv{a}=\left(\frac{1}{2}\cdot 4, \frac{1}{2} \cdot (-1)\right) = \left(2,-\frac{1}{2}\right)$

$4\cdot \vv{a}=(4\cdot 4, 4 \cdot (-1)) = (16,-4)$

Bu nedenle pozitif sayılarla çarpılan vektörler orijinal vektörle aynı yön ve yöne sahiptir. Ve negatif sayılarla çarpılan vektörler orijinal vektörle aynı yöne ancak zıt yöne sahiptir.

Aynı yönde ve aynı yöndeki vektörler:

$\displaystyle 2\vv{a}, \ 4\vv{a}$

$\displaystyle \frac{1}{2}\vv{a}$

Yönü aynı fakat anlamı farklı olan vektörler:

$-3\vv{a}$

Son olarak vektörleri uzunluklarına veya eşdeğer olarak modüllerine göre sıralamalıyız. En uzun uzunluktaki vektör (veya en büyük modül), daha büyük bir sayıyla (mutlak değerde) çarpılmış olan vektör olacaktır ve en kısa uzunluktaki vektör (veya en küçük modül), daha küçük bir sayıyla çarpılmış olan vektör olacaktır. sayı (mutlak değer olarak). Yani uzunlukların sırası şöyledir:

$\displaystyle \begin{vmatrix} \displaystyle\frac{1}{2}\vv{a}\end{vmatrix} <\lvert 2\vv{a}\rvert < \lvert -3\vv{a}\rvert < \lvert 4\vv{a}\rvert$