Bu sayfada iki vektörün düzlemde grafiksel ve sayısal olarak nasıl toplanacağı açıklanmaktadır. Bunları grafiksel olarak eklemenin 3 yolu vardır: paralelkenar, baştan sona ve çokgen yöntemi. Ek olarak, vektör toplama ve vektör toplamanın tüm özelliklerine ilişkin çözülmüş alıştırmalar da bulacaksınız.
İki vektör grafiksel olarak nasıl eklenir?
Temel olarak vektörleri grafik gösterimlerinden eklemenin iki yolu vardır. Her iki şekilde de aynı sonuç elde edilir, ancak bazıları bunları tura-kuyruk yöntemini kullanarak, diğerleri ise paralelkenar yöntemini kullanarak toplamayı tercih eder. Bu nedenle tercih ettiğiniz yöntemi seçebilmeniz için size iki yöntemi açıklayacağız. 😉
Öte yandan bu iki yöntem iki vektörü toplamak için kullanılıyor ama ikiden fazla vektör eklemek istersek ne olur? Bu nedenle paralelkenar yönteminin art arda kullanılmasından oluşan çokgen yönteminin kullanılması gereklidir. Bunun açıklamasını tura-kuyruk ve paralelkenar yöntemlerinden sonra da bulacaksınız.
Paralelkenar yöntemi veya kuralı
Paralelkenar kuralı veya paralelkenar yöntemi (veya paralelkenar yasası), iki vektörün toplamını çok basit bir şekilde bulmanızı sağlayan grafiksel bir prosedürdür. Bu işlemi uygulamak için izlenecek adımlar şu şekildedir:
- Öncelikle vektörleri çizip aynı uygulama noktasına konumlandırıyoruz, yani her iki vektörün orijinlerini aynı noktaya yerleştiriyoruz.
- Daha sonra bir vektörün sonuna diğer vektöre paralel bir çizgi çizeriz. Ve adımı diğer vektörle tekrarlıyoruz. Bu nedenle bir paralelkenarın çizimini elde edeceğiz (kuralın adı da buradan gelmektedir).
- Son olarak toplamın sonucu, ortak orijinden iki paralel çizginin kesiştiği noktaya giden vektör olacaktır.
Paralelkenar kuralıyla iki vektörün toplandığı aşağıdaki genel örneğe bakın:

Vektörlerin toplamının sonucu, paralelleriyle oluşturdukları paralelkenarın köşegenidir.
baş ve kuyruk yöntemi
Baş ve kuyruk yöntemi veya üçgen yöntemi olarak da bilinen, iki vektörün grafiksel olarak toplanabileceği başka bir prosedürdür. Bu durumda izlenecek adımlar şunlardır:
- Eklenen bir vektörü taşıyın ve orijini, eklenen diğer vektörün tam sonuna gelecek şekilde yerleştirin.
- Vektör toplamanın sonucu, ilk eklenen vektörün başlangıcından diğer vektörün sonuna giden segmenttir. Yakından bakarsanız, iki vektörün ve vektörün eklenmesiyle bir üçgen tamamlanır.
Baştan sona yöntemi kullanılarak vektör toplamaya bir örnek:
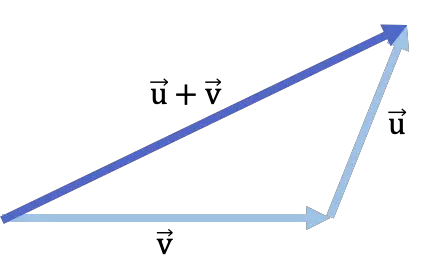
çokgen yöntemi
İki vektörün toplamını grafiksel olarak nasıl çözeceğimizi gördükten sonra, ikiden fazla vektörümüz olduğunda bunun nasıl yapıldığını göreceğiz.
Üç veya daha fazla vektör eklemek istediğinizde işlemin hesaplanmasını hızlandıracak bir teknik vardır. Bu tekniğe çokgen yöntemi denir ve baştan sona yöntemin başarıyla uygulanmasından oluşur:
- Öncelikle her vektörü birbiri ardına yerleştirmemiz gerekiyor, böylece bir vektörün orijini diğer bir vektörün sonuyla çakışıyor. Bunları yerleştirdiğimiz sıra önemsizdir.
- Ve toplamın sonucu, ilk vektörün başlangıcını son vektörün sonuna birleştirerek elde edilen vektördür.
4 vektörün toplandığı aşağıdaki örneğe bakın:
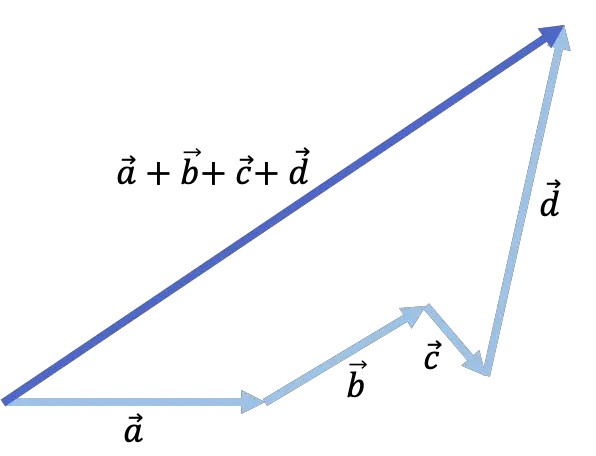
İki vektörün toplamını sayısal olarak hesaplayın
Vektörlerin geometrik olarak nasıl toplandığını öğrendikten sonra, bir vektör toplamının sayısal veya cebirsel olarak nasıl hesaplanacağını göreceğiz.
İki vektörü sayısal olarak toplamak için ilgili bileşenlerini eklemelisiniz. Veya diğer bir deyişle iki vektörün X koordinatları birbirine eklenir ve Y koordinatları ile aynı olur.
![]()
![]()
Örneğin, vektörler arasındaki toplam
![]()
Ve
![]()
Doğu:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(1,2) +(5, 3) \\[2ex] & = (1+5,2+3) \\[2ex] & = \bm{(6,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c0813ac0f7ad7fafa1f20b6284430a5_l3.png)
Öte yandan iki vektörün vektörel toplamının, vektörlerin modüllerinin toplamı ile aynı olmadığını, aslında sonuçların tamamen farklı olduğunu da unutmamalıyız. İki işlem arasındaki farkları vektör büyüklüğünün (vektör büyüklüğü de denir) özelliklerinde görebilirsiniz.
Vektör Özellikleri Ekle
Vektör toplama aşağıdaki özelliklere sahiptir:
- İlişkisel özellik : Birkaç vektörün toplamı arasına parantez koymak işlemin sonucunu değiştirmez.
![]()
- Değişme Özelliği – Vektör çıkarma işleminin aksine, iki vektör arasındaki toplama işleminin sonucu, bunların toplanma sırasından bağımsızdır.
![]()
- Karşıt elemanın özelliği : Bir vektör artı onun tersinin, yani olumsuzunun toplamı 0’a eşittir.
![]()
- Nötr elemanın özelliği : Açıkçası, herhangi bir vektör artı boş veya boş vektör, vektörün kendisine eşdeğerdir:
![]()
Çözülmüş vektör toplama problemleri
1. Egzersiz
Vektörlerin toplamını grafiksel olarak hesaplayın
![]()
Ve
![]()
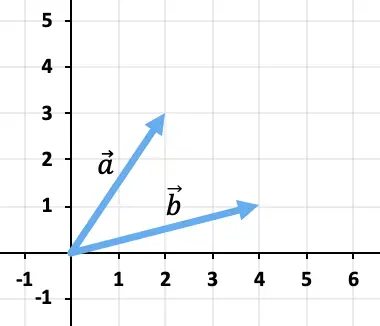
İki vektörü toplamak için baş ve kuyruk kuralını kullanacağız. Bu nedenle vektörün kökenini yerleştireceğiz
![]()
vektörün sonunda
![]()
ve toplam, koordinatların başlangıcından sonuna kadar giden vektör olacaktır.
![]()
Bu nedenle vektör toplamanın sonucu:
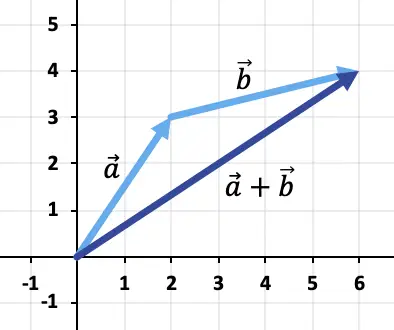
Alıştırma 2
Vektörlerin toplamını grafiksel olarak çözün
![]()
Ve
![]()
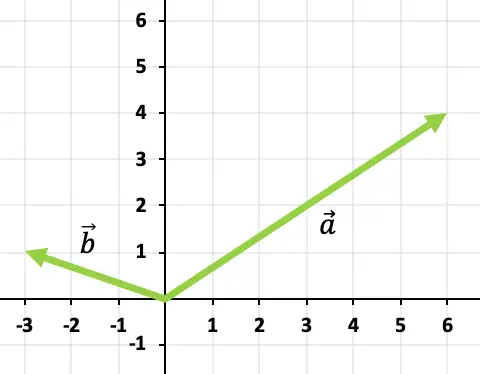
İki vektörü eklemek için tura-kuyruk kuralını kullanacağız. Bu nedenle vektörün kökenini bulacağız
![]()
vektörün sonunda
![]()
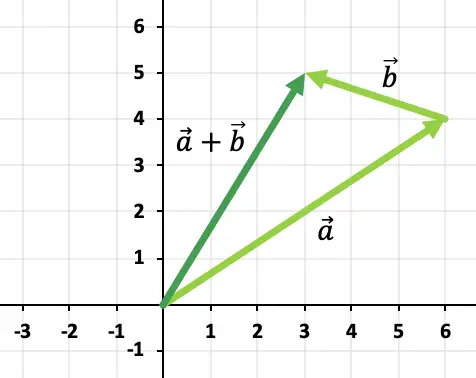
ve toplam vektörü eksenlerin başlangıç noktasından sonuna kadar olan vektör olacaktır.
![]()
Bu nedenle vektör toplamanın sonucu:
Alıştırma 3
Grafikte temsil edilen tüm vektörlerin eklenmesinden elde edilen vektörü grafiksel olarak belirleyin:
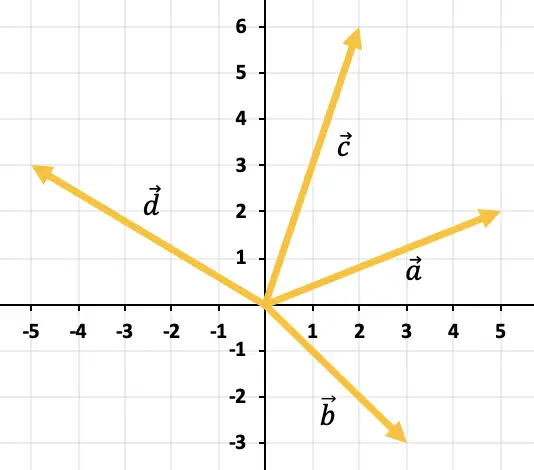
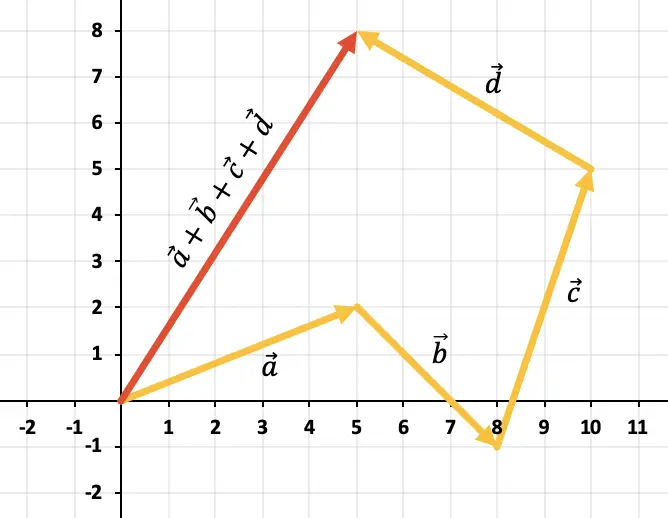
Grafiğe 2’den fazla vektör eklemek için çokgen kuralını kullanmanız gerekir. Bu nedenle vektörleri sürekli kalacak şekilde, yani birbiri ardına hareket ettirmeliyiz (sıra önemsizdir). Yani tüm vektörlerin toplamı, ilk vektörün başlangıcından son vektörün sonuna kadar giden vektör olacaktır.
Yani 4 vektörün toplamının sonucu kırmızıyla gösterilen vektördür:
Alıştırma 4
Aşağıdaki vektörlerin toplamını sayısal olarak bulun:
![]()
İki vektörü sayısal olarak eklemek için ilgili koordinatlarını eklemelisiniz:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}& =(3,-2)+(-4,6) \\[2ex] & = (3+(-4) ,-2+6)\\[2ex] & =\bm{(-1,4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6299484debe49023b686839df40f88b_l3.png)
Alıştırma 5
Aşağıdaki vektörlerin toplamını analitik olarak hesaplayın:
![]()
Vektörleri sayısal olarak eklemek için ilgili koordinatlarını eklemelisiniz:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}+\vv{c}+\vv{d}& =(-1,3)+(4,0)+(2,-5)+(3,-2) \\[2ex] & = (3,3)+(2,-5)+(3,-2) \\[2ex] & = (5,-2)+(3,-2)\\[2ex] & =\bm{(8,-4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05b7c1606bfa3d94d080163a40dc4412_l3.png)